每个激活函数的输入都是一个数字,然后对其进行某种固定的数学操作。激活函数给神经元引入了非线性因素,如果不用激活函数的话,无论神经网络有多少层,输出都是输入的线性组合。
激活函数的发展经历了Sigmoid -> Tanh -> ReLU -> Leaky ReLU -> Maxout这样的过程,还有一个特殊的激活函数Softmax,因为它只会被用在网络中的最后一层,用来进行最后的分类和归一化。
Sigmoid

它输入实数值并将其“挤压”到0到1范围内,适合输出为概率的情况。

面试点:
- Sigmoid函数的导数 s ( x ) ′ = s ( x ) ( 1 − s ( x ) ) ∈ [ 0 , 0.25 ] s(x)'=s(x)(1-s(x)) ∈ [0, 0.25] s(x)′=s(x)(1−s(x))∈[0,0.25]
- 假设 a = g ( z ) a=g(z) a=g(z), L ( a , y ) L(a,y) L(a,y)是交叉熵Loss, g g g是Sigmoid函数:反向传播时,Loss对 a a a求偏导, a a a对 z z z求偏导…实现反向传播。其中, a a a对 z z z求偏导,即为面试点 1 1 1的结果。
- Sigmoid函数饱和使梯度消失。当神经元的激活值在接近0或1处时会饱和,在这些区域梯度几乎为0,由 1 1 1可得。这就会导致梯度消失,几乎就没有信号通过神经传回上一层。
- Sigmoid函数非0中心。关于
w
w
w各分量在梯度更新的过程中,将会同时增大或减小,如果随机初始化到第四象限,将会导致权重更新时出现低效率
z
z
z字型梯度更新趋势。下图为推导过程:

Tanh

它将实数值压缩到[-1,1]之间。

Tanh解决了Sigmoid的输出非0中心的问题,但仍然存在饱和问题。
为了防止饱和,现在主流的做法会在激活函数前多做一步Batch Normalization,尽可能保证每一层网络的输入呈均值较小、0中心的分布。
ReLU

相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用;sigmoid和tanh在求导时含有指数运算,而ReLU求导几乎不存在任何计算量。

对比sigmoid类函数主要变化是:
- 单侧抑制
- 相对宽阔的兴奋边界
- 稀疏激活性
存在问题:
ReLU单元比较脆弱并且可能“死掉”,而且是不可逆的,因此导致了数据多样化的丢失。通过合理设置学习率,会降低神经元“死掉”的概率。
Softmax

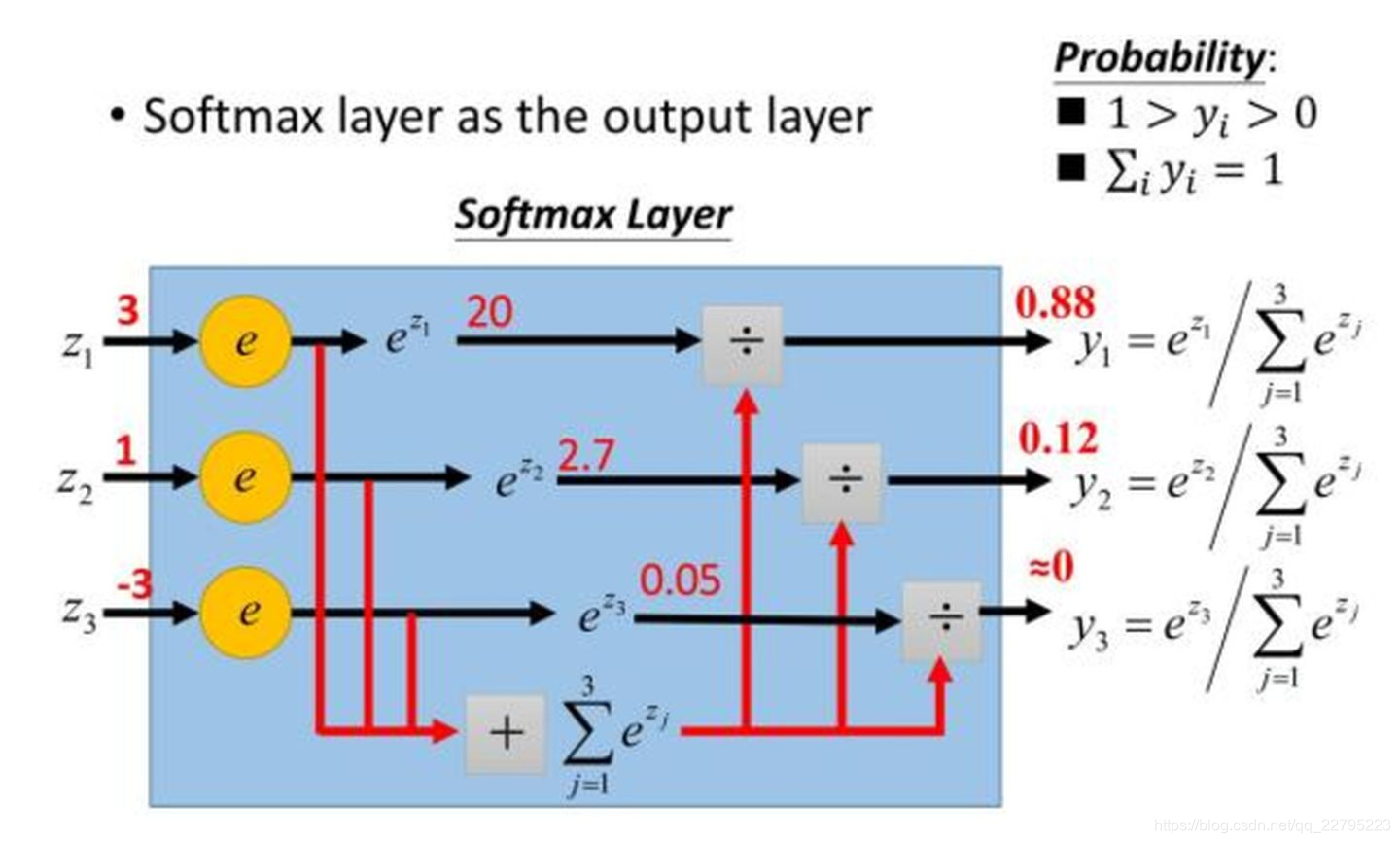
Softmax是Sigmoid的扩展,当类别数k=2时,Softmax回归退化为Logistic回归。
面试补充
1. 为什么用Softmax怎么不用Hardmax?反向传播有什么不同?(阿里面试中问过)
Hardmax就是简单的大于阈值为1,小于阈值为0,反向传播时,导数为0,无法进行反向传播。
而Softmax在反向传播时,则可以正常进行梯度更新。



























 2286
2286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










