LeetCode 48. Rotate Image

题目：

你有一个n x n二维矩阵表示一个图像。将图像旋转90度(顺时针方向)。

你必须原地旋转图像，这意味着你必须直接修改输入2D矩阵。不要分配另一个2D矩阵，做旋转。

You are given an n x n 2D matrix representing an image.

Rotate the image by 90 degrees (clockwise).

Note: You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

 

Given input matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

rotate the input matrix in-place such that it becomes:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

Given input matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

rotate the input matrix in-place such that it becomes:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

思路：

对于一个数的逆时针来说，会涉及到数组中的另外三个数，因此，每次在旋转时，从外到内的每一层，都以四个为一组进行旋转

具体为：

先用temp变量存储当前要旋转的一组的第一个数（如 matrix[x][y]）

再将matrix[Max-y+x][Min] 放到 matrix[x][y] 位置

再将matrix[Max][Max-y+x] 放到 matrix[Max-y+x][Min] 位置

再将matrix[y][Max] 放到 matrix[Max][Max-y+x] 位置

最后将temp放到 matrix[Max][Max-y+x] 位置

且：

设第i轮时，该层一行有n个数，但是只需要进行n-1次旋转，因为在第1次旋转时已经将第n个数旋转了

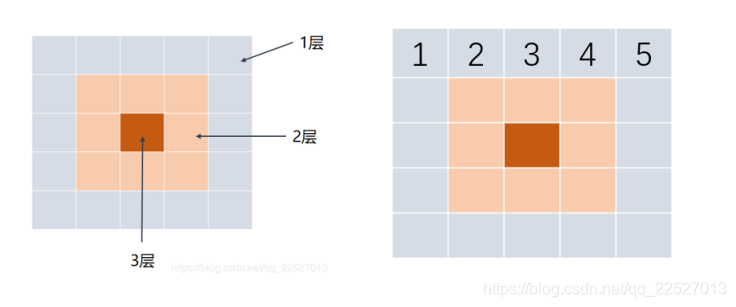
在交换时，先交换外圈，再往里交换

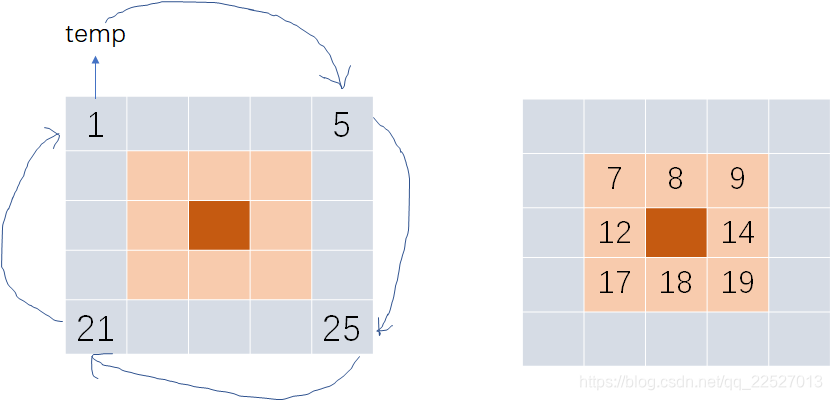
需要注意的是，标粗位置——

Max-y指的是当前坐标与所需要替换的位置的距离，但是由于当前坐标的基础坐标为x，所以需要 基础+距离 即x+（Max-y）

再将matrix[Max-y+x][Min] 放到 matrix[x][y] 位置

再将matrix[Max][Max-y+x] 放到 matrix[Max-y+x][Min] 位置

再将matrix[y][Max] 放到 matrix[Max][Max-y+x] 位置

最后将temp放到 matrix[Max][Max-y+x] 位置

 

代码：

class Solution {
    public void rotate(int[][] matrix) {
        for(int x=0;x<matrix.length/2;x++) {
            int Max = matrix.length-1-x;
            int Min = x;
            for(int y=x;y<Max;y++) {
                int temp = matrix[x][y];
                matrix[x][y] = matrix[Max-y+x][Min];
                matrix[Max-y+x][Min] = matrix[Max][Max-y+x];
                matrix[Max][Max-y+x] = matrix[y][Max];
                matrix[y][Max] = temp;	
            }
        }
    }
}