GAN学习：GAN/DCGAN原理、公式推导及实践

GAN学习：GAN/DCGAN原理、公式推导及实践

生成对抗网络（GAN）是深度学习领域一个相当有趣的内容。最近补习了一下相关的论文，也推了下公式、做了一点简单的实践，因此写了这篇文章来对GAN进行介绍。大致分为三个部分

1. GAN：介绍GAN的思想、原理，以及公式推导和训练过程
2. DCGAN：引入DCGAN，介绍基于深度卷积网络的GAN，并谈一下自己对GAN的理解
3. 动漫头像生成：使用Pytorch，实现了一个对DCGAN的简单应用

一、GAN

GAN原理简介

GAN的起源应该是Ian Goodfellow大牛的这篇paper。
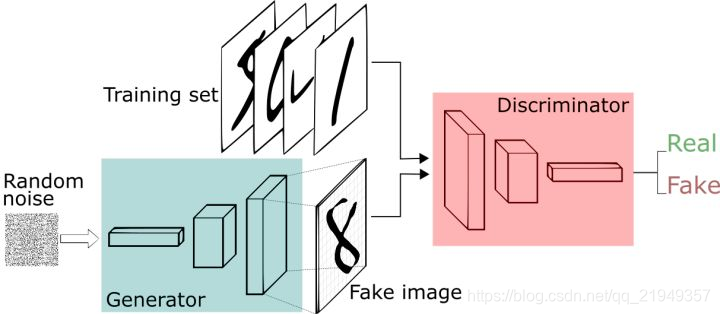
GAN的基本原理很简单，以图片生成领域为例，整个网络由两个部分构成：G(Generator)，即生成器，以及D(Discriminator)，判别器。
借用这篇博客的图片可以很清晰地看到整个过程，G接收按照一定概率分布生成的随机分布作为噪声，生成和真实数据尽可能类似的图片；而D则负责从真实数据集和生成的图片中，区分真假。两者的目的相反，由此构成了一个博弈过程，这就是生成对抗网络名称的由来。

直观上来说，随着训练的过程，D的分辨能力会得到提高，而这又会迫使G生成更加逼真的样本，最后理想情况下，生成的虚假样本和真实样本基本上完全一致，D对任意样本判断其属于真实样本的概率都是0.5，等同于随机猜。GAN的一文中对这一过程给出了示意图：

其中，黑色虚线可以视作真实样本的分布(离散的)，而绿色实线则是生成器生成样本的分布。蓝色虚线可以看作是分类器，用于输出给定x的情况下，最后样本属于真实类别的概率。由于一开始蓝色虚线性能不佳，此时即使生成了样本也无从判断样本的逼真程度，因此往往先训练分类器，达到(b)图中比较好的效果。在分类器如图(b)中所示，能够根据给定的x判断属于哪个分布后，再训练生成器就可以让生成器生成的分布去拟合真实样本的分布，最后达到(d)当中的理想效果。

GAN的应用非常广泛，包括但不限于针对监督学习样本稀缺下的数据增广，辅助半监督学习，以及大量涉及到生成和图片翻译的领域。例如影片的修复、上色、辅助拍摄，超分辨率，动漫领域的动画生成和虚拟主播等等。

数学描述

针对GAN的目标，原论文给出了如下数学描述，假定用于生成的噪声分布是$p_z(z)$，真实数据分布是$p_x(x)$，同时生成器和辨别器分别为G和D，则GAN的目标可以通过如下公式描述：

这里的公式形式其实和常见的交叉熵损失函数很像，但要注意没有负号。D(x)表示x来源于真实数据的分布，理想情况下，D(x)=1，logD(x)=0。若是分类器不理想，则D(x)输出越小，logD(x)则会越小。G(z)表示噪声经过生成器后生成的样本，D(G(z))则是分类器认为生成样本属于真实样本的概率，理想情况下这个数值为0，但当性能越不好，D(G(z))越大，log(1-D(G(z)))就会越小。总而言之，后面两项期望的和越大，分类器识别能力越好。
再观察估值函数V(G,D)前面的min/max，就很明显了，最终的目标是求外面的minG，G的目标是让V最小，达到以假乱真的目的；而内部嵌套的maxD，则代表D是在G给定的情况下，最大化V，即给定生成器，得到识别能力最好的分辨器。

公式推导

得到了GAN的数学化建模后，我们需要确定3个问题：

1. 假设G和D有足够的容量(没有参数限制)，该问题是否真的有解呢？要知道，如果这个问题在数学上就无解，那么我们再怎么训练也是没有意义的。
2. 对于DNN这种很难进行数学建模来描述G/D的模型来说，怎么逼近解？
3. 解是否可达到的问题。

我们将在这部分讨论第1个问题，并在下一个部分讨论第2个问题。第3个问题论文中有过一定的讨论，由于比较复杂我们在这篇博客里暂时不做总结。
先看论文怎么谈第一个问题的，对于第一个问题，要分两步求解：在G固定的情况下，求出最佳的分类器$D_G^{\ast }(x)$；然后将最佳分类器带回，证明该问题的有解性。

第一步：求最优D
展开V(G,D)并对第二项进行换元

不难看出来，第一行其实就是原有的V(G,D)对期望公式的展开。问题是第二行是怎么得到的？一个直观的思路是令g(z)=x，并进行换元，具体的公式推导参考这篇博客。这里的$p_g(x)$实际上代表了由z生成的x的分布，和二者都有联系。我们之所以在这里不展开说这个换元，是因为这个方式要求生成器必须可逆，而对很多问题，尤其是DNN来说这基本是不可能的。对于这一问题可以参考机器之心里的结论。完整的推导比较复杂，有兴趣的同学可以到这里自行推导。
按照paper中的符号，我们令：$p_{data}(x)=a,p_g(x)=b,D(x)=y$，那么可以得到积分内的积分函数：
$$f(y)=alog(y)+blog(1-y)$$
对f(y)求一阶导和二阶导，并求出极值点：
$$f^{\prime }(y)=\frac{a}{y}-\frac{b}{1-y}$$
$$f^{\prime }(y)=0\Rightarrow y=a+$$