【笔记】信息论基础

一. 相关概念

1. 各种熵

（1）自信息

信息理论认为，一个事件的信息量大小和它发生的概率相关。发生概率越大，信息量越小。发生概率越小，信息量越大。根据信息量要非负，可以相加等一系列性质，反正最后香农爸爸发现，负log函数是唯一满足要求的。因此自信息定义为

画成图的话，大概就是和概率成一个反比的样子。

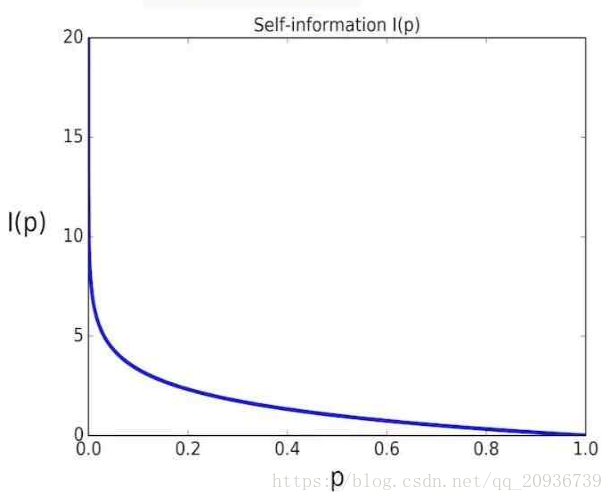
(2)信息熵

对于一个事件X，比如说明天是晴天还是阴天，我对这个事件预测的话，把握有多大呢，也就是说事件X可能发生的结果确定性大不大。

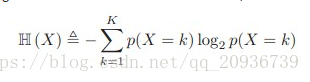
 实际上是从一维积分变成了二维积分。

需要注意的是：

-----> H（X） = I（X,X），也就是X的信息熵和他自己的互信息相等。

-----> p=0的时候，PlogP = 0.

 

（3）条件熵

条件熵的意义为，我们可以通过与X相关的Y来增加对X的了解，在知道X的情况下，Y不确定性将减小为H（Y|X）。

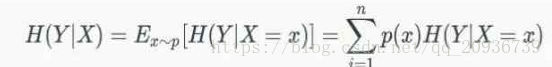
（4）互信息

互信息通俗的来讲，就是从一个变量X可以获得多少关于Y的信息。 

I（X;Y）=

 

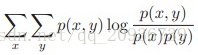
互信息也是一个二维期望，此处的概率是P（x，y）

上面这几种熵的关系如下图：

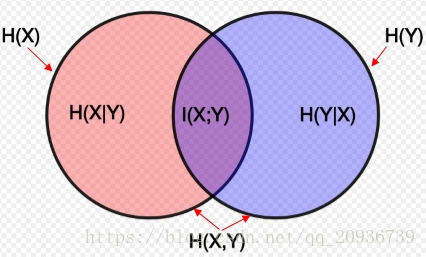
（5）交叉熵 和 KL散度

先贴一个知乎回答。

https://www.zhihu.com/question/41252833

交叉熵在机器学习中很常用。定义为

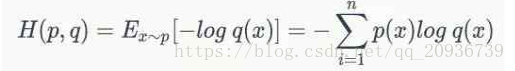
交叉熵的意义为：

我们通过学习，分析出的X的分布为q，而实际上，X分布为p，真实的熵H（p）为- p log p（x）。因此，如果认为是编码的话，实际的编码长度为H（p，q）而不是H（p）

从机器学习的角度，我们希望估计的分布q和p应该尽量一致，此时 H(p，q)=H（p）

而根据Gibbs' inequality可知，H(p,q)>=H(p)恒成立，也就是 交叉熵可以作为评估我们的预测q和真实情况p是否相似，所以交叉熵经常被用作损失函数。

而这个差值H(p,q)-H(p)被称为是KL散度，计算为

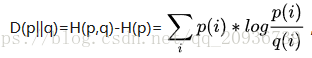
（二）马尔可夫链和DNN网络

马尔科夫链通俗的定义来讲，就是不断随机变化的状态序列，而且下一状态只与上一状态有关。维基百科给出了一种数学表达

和DNN比较的话，s可以看作是输入，输入Y是将X作用于s，在神经网里就是加权，通过激活函数的过程。而神经元只与上一层有链接，因此符合马尔可夫性质。

因此 DNN网络可以被当作马尔可夫。

（三）Data Processing Inequality （DPI）

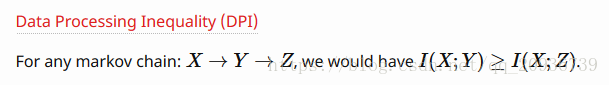
马尔可夫链的转移过程可以认为是对数据进行处理的过程，数据处理过程中，互信息只会丢失。大概意思就是一旦数据被处理了，和源数据相关性就会越来越弱。

这里给一篇文章，讨论既然降维等算法处理后，互信息都少了，对于传统方法性能却变好了，而对于神经网络，使用原始数据更好。

http://freemind.pluskid.org/machine-learning/data-processing-inequality/

简单总结一下作者的思路：

信息量大不代表信息有用。传统方法分析能力弱，降维等算法是帮助传统方法提取出真正有用的信息。而神经网络非常善于抽丝剥茧，能够分析出复杂数据所包含的信息，降维过程是人工的，因此必然有一些有价值的信息会被丢失。所以传统方法需要对数据进行各种处理，留下大部分有用的信息。而神经网络强大的能力使得他可以自己分析出未经处理的数据中的有用信息，人工处理反而会导致性能下降。