离散数学干货

定义

简单图: 既不含平行边也不含自环的图。且|E|<=|V|(|V|-1)/2

完全图: 每对顶点之间都恰连有一条边的图

关联矩阵：反应点与边连接情况的行列式

如何判断两图是否同构：写出关联矩阵，通过行列互换，若一致则同构

握手定理：图所有节点的度数和等于边数的两倍。意味着图的度数列之和应该为偶数。

简单图的度数列判定方法：满足|E|<=|V|(|V|-1)/2且满足握手定理

图的生成树：连通所有点且不含有圈的树

图的生成子图：如果一个图G的子图G’包含了G的所有结点,则称该子图为G的生成子图

注意生成树和生成子图区别

离散数学图论中的“同胚”是什么意思？
答：同胚，简单地讲，就是一个图形，可以通过连续变形（例如，拉伸，弯曲），变成另一个图形。
与K5同胚的图到底是什么样的？
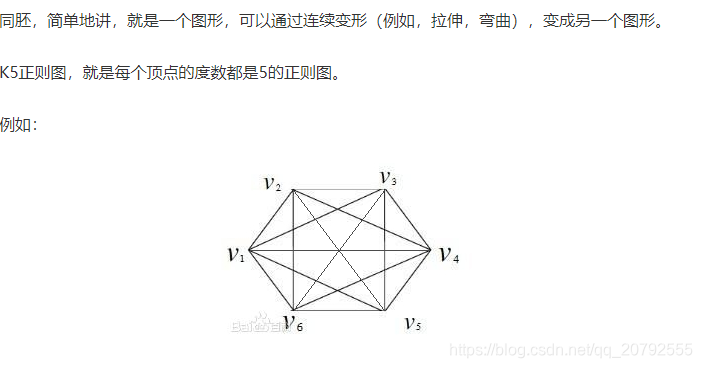
答：K5正则图，就是每个顶点的度数都是5的正则图。

边数集为空集的图叫零图 在此基础上结点数为1的叫平凡图

平凡图也是完全图

空图：没有点的图

零图：没有边的图

平凡图：一阶零图

二部图判定方法：染色法，首先取一个点染成白色，然后将其相邻的点染成黑色，如果发现有相邻且同色的点，那么就退出，可知这个图并非二分图。

判定强连通：图D存在经过__每个顶点至少一次__的回路

判定单连通：图D存在经过__每个顶点至少一次__的通路

判定弱连通(连通)：去掉方向后图连通则为弱连通

欧拉定理：(平面-2等于边数-顶点数)在任何一个规则球面地图上，用 R记区域个 数 ，V记顶点个数 ，E记边界个数 ，则 R+ V- E= 2，这就是欧拉定理

点连通度：在一个具有N个点的图G中，在去掉任意k-1个顶点后（1<=k<=N），所得的子图仍然连通，去掉K个顶点后不连通，则称G是K连通图，K称作图G的连通度，记作K（G）。

边连通度：同理点连通度，记作λ(G)。

delta：最大度；segma:最小度；+：出度；-：入度

简单通路：边各异

简单通路：边各异

正则图：正则图是指各顶点的度均相同的无向简单图。

判定哈密顿通路：（自己瞎想的）：每个点连接的边数不少于图的顶点数-1；意思是至少是一个完全图。

哈密顿回路：（自己瞎想的）：每个点连接的边数不少于图的顶点数；意思是在完全图的基础上每对点之间至少存在一条平行边。

哈密顿图判定：

至少存在一条不重复经过所有点的回路的图。

图的同胚：

与同构同，差异在于，同构是代数学中的概念，同胚是拓扑学中的概念。

图的基本概念：

​

n阶完全无向图表示为Kn，其边数为Cn2

n阶完全有向图边数为2Cn2

5-正则图：每个顶点的度数都相同且为5

集合的定义：满足某条性质的个体放在一起组成的集合

集合的特征：1.互异性，2.无序性，3.有多重表现形式，4.确定性

幂集的定义：设A为一个集合，称由A的所有子集组成的集合为A的幂集，记为P(A)。性质：若A中有n个元素，则|P(A)|=2^n