机器学习一些基础概念总结

还是因为面试，恶补了一下机器学习基础知识

回归问题vs分类问题

首先最基础的需要分辨该问题是回归vs分类。
回归需要输出一个度量值d=F(ytrue,ypred)，这是一个连续数。常见的回归问题有，预测寿命，预测收入等等。
分类是判断类别，输出是不连续的数。常见的分类问题有，这是正确或者错误，这是小鸟或者猫等等。

逻辑回归

背景：线性回归是根据逻辑回归进化来的，我们从线性回归开始介绍。线性回归的方程式：

Y=a0+a1x1+a2x2+…+an*xn

线性回归将所有的数据都纳入预测范围，一旦有异常的数据，比如很大的数据，会对预测结果造成很大的影响。
对线性回归的改进：
通过sigmod函数，缓解线性回归对异常数据敏感的问题。如下图所示为sigmoid函数。

求最优解
最优化的问题常用求导，线性回归比较好求导，但是逻辑回归不好求导，于是用最大似然估计（交叉熵损失函数）来求。而最优化计算使用梯度下降法。

SVM

简介
SVM主要用于处理二分问题，将数据的间隔最大化。针对线性问题如下图所示，可以直接使用SVM；而针对非线性问题，通过非线性的核转化为线性问题。

优化方法
为了计算数据点到平面的最小距离，使用拉格朗日乘子法。
具体方法：
1）将有约束的原始目标转为无约束的拉格朗日函数
2）得到w和b
3）得到超平面
4）分类决策函数（分为线性问题和非线性问题）

模型融合

1.bagging

特点
分类器之间无依赖，可并行计算
具体过程
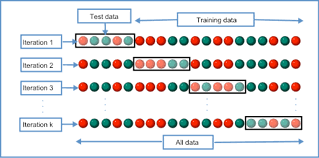
将训练集在划分为多个训练集和验证集，也即k-fold，
具体步骤：
1）将训练集划分为K个互相独立的训练集和验证集，如下图所示，也即生成k个模型
2）对结果进行统计，如果是回归问题采用均值，如果是分类问题，进行投票

常用模型
随机森林

2.boosting

对于分类问题，提升树的决策树是二叉决策树，对于回归问题，提升树中的决策是二叉回归数。采用的是前向分步算法。关于损失函数，回归问题采用平方差，分类问题采用指数损失。
提升树的思想就是先粗鲁给一个值，再逐步拟合到目标。每一棵树学习的是之前所有树结论和残差，这个残差是一个加预测值后能达到真实值的累加值。

特点
分类器之间有依赖，必须串行
具体过程
训练的目的是找到一个f拟合上一轮的残差，减小在上一轮训练正确的权重，增加错误样本的权重
常用模型
Adaboost、GBDT、XGBT、XGboost、lightgbm
梯度提升树（GBT）
核心思想：利用损失函数的负梯度在当前模型的值作为残差的近似值，本质上是对损失函数进行一阶泰勒展开，从而拟合一个回归树。
另外，梯度提升树用于分类模型时，是梯度提升决策树GBDT；用于回归模型时，是梯度提升回归树GBRT，二者的区别主要是损失函数不同。
XGboost：用到了二阶泰勒展开，加入了正则项

3.stacking

具体过程
每个基模输出组合作为特征向量进行训练

评判指标

首先定义

TP:正确的匹配数目

FP:误报，没有的匹配不正确

FN:漏报，没有找到正确匹配的数目

TN:正确的非匹配数目

1.准确率（Accuracy）

（TP+TN）/总
在正反样本不成比例的情况下，这个没用，比如99个正样本，1个负样本，系统可以学习为只输出正样本就好。

2.精确率(Precision)

TP/（TP+FP）
可以理解为预测结果的置信度

3.召回率(Recall)

TP/（TP+FN）

4.F1-score

F值 = 精确率 * 召回率 * 2 / ( 精确率 + 召回率) （F 值即为精确率和召回率的调和平均值）

5.AUC

对于0，1两类分类问题，一些分类器得到的结果往往不是0，1这样的标签，如神经网络得到诸如0.5，0.8这样的分类结果。这时，我们人为取一个阈值，比如0.4，那么小于0.4的归为0类，大于等于0.4的归为1类，可以得到一个分类结果。同样，这个阈值我们可以取0.1或0.2等等。取不同的阈值，最后得到的分类情况也就不同。如下面这幅图：

　　蓝色表示原始为负类分类得到的统计图，红色表示原始为正类得到的统计图。那么我们取一条直线，直线左边分为负类，直线右边分为正类，这条直线也就是我们所取的阈值。阈值不同，可以得到不同的结果，但是由分类器决定的统计图始终是不变的。这时候就需要一个独立于阈值，只与分类器有关的评价指标，来衡量特定分类器的好坏。还有在类不平衡的情况下，如正样本有90个，负样本有10个，直接把所有样本分类为正样本，得到识别率为90%，但这显然是没有意义的。如上就是ROC曲线的动机。

遍历所有的阈值可以得到相应的ROC曲线如下图所示。

6.ROC

AUC值为ROC曲线所覆盖的区域面积，显然，AUC越大，分类器分类效果越好。