梯度下降算法在线性回归中的应用

线性回归符号约定

一元线性回归常见表达式：
$$y=kx+b$$
将上式中的$y$变为$h_{\theta }(x)$，$b$变为${\theta }_0$，$a$变为${\theta }_1$，$x$变为$x_1$，则变为：
$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1$$
为了数学表达规范，在${\theta }_0$后面乘上$x_0$，并且令$x_0=1$则变为：
$$h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1$$
将上述式子推广到多元，就得到了：
$$h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n$$
写成求和符的形式：
$$h_{\theta }(x)=\sum _{i=0}^n{\theta }_i{x}_i$$
写向量相乘的形式（在不进行说明的情况下，向量为列向量）：
$$\begin{gathered} h_{\theta }(x)={\theta }^{T}x \\ {\theta }^T=\left[\begin{array}{c}{\theta }_0,{\theta }_1,{\theta }_2,\cdots ,{\theta }_n\end{array}\right] \\ x=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ ⋮\\ x_n\end{array}\right] \end{gathered}$$
请注意，$x_0$是始终等于1的，这一项表示线性函数的常数项。总结一下上面的形式，得到线性回归的假设函数：
$$h_{\theta }(x)=\sum _{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$$
线性回归的损失函数定义为预测值$h_{\theta }(x)$与目标值$y$之间差值的平方，数学表达式为：
$$L(\theta )=(h_{\theta }(x)-y{)}^2$$
上面的损失函数用来计算单个点与真实值的偏差，那么对于全部数据的损失则通过代价函数来计算，数学表达式为：
$$\begin{array}{rl}J(\theta )& =\frac{1}{2}\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2\\ & =\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2\end{array}$$

其中，$m$表示样本数量，$x^{(i)}$表示第$i$个样本，是一个列向量。抛开前面的$\frac{1}{2}$，实际上就是在计算所有样本预测值与目标值之间差值平方和的均值。至于为什么要多乘$\frac{1}{2}$​，是为了后面对代价函数求导的时候简化计算，等到后面大家就知道了。

梯度下降法

关于梯度下降算法的数学推导这里就不做太多的解释，直接以一个例子来说明。比如求
$$J(\theta )={\theta }^2+2\theta +5$$
最小值。

则梯度为$J(\theta )$对$\theta$​的偏导：
$$\nabla J(\theta )=\frac{\partial J(\theta )}{\theta }=2\theta +2$$
给定学习率$\alpha =0.06$，$\theta$随机初始化为3（下式中$\theta$的上标$(i)$表示$\theta$第$i$次迭代后的数值），则梯度下降算法的第一次迭代：
$$\begin{array}{rl}{\theta }^{(1)}& ={\theta }^{(0)}-\alpha \nabla J({\theta }^{(0)})\\ & =3-0.06\times (2\times 3+2)\\ & =2.52\end{array}$$
第二次迭代：
$$\begin{array}{rl}{\theta }^{(2)}& ={\theta }^{(1)}-\alpha \nabla J({\theta }^{(1)})\\ & =2.52-0.06\times (2\times 2.52+2)\\ & =2.0976\end{array}$$
后面的我就不继续写了，经过一定次数的迭代，函数的值会持续变小，最终会收敛到最小值（注意！因为这里是一个比较简单的凹函数，所以我用了最小值的概率。实际上在大部分情况下应该为极值，因为对于复杂的问题，很难得到全局最值，只能得到局部最值，也就是极值）

梯度下降算法求解线性回归

从上面整理的线性回归==代价函数$J(\theta )$==来看，代价函数$J(\theta )$越小，说明函数拟合的越好。那么我们使用梯度下降算法，让代价函数损失最小化。假设目标函数是多元线性回归，也就是存在多个$\theta$，且$\theta$的数量为$j$个，${\theta }_j$表示第$j$个$\theta$的值。
$$\begin{array}{rl}\frac{\partial }{\partial {\theta }_j}J(\theta )& =\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2\\ & =\frac{1}{2m}\times \left[2\times \sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\right]\times \frac{\partial }{\partial {\theta }_j}\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\\ & =\frac{1}{2m}\times \left[2\times \sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\right]\times \frac{\partial }{\partial {\theta }_j}\left(\sum _{j=0}^n{\theta }_j{x}_j^{(i)}-y^{(i)}\right)\\ & =\frac{1}{m}\sum _{i=1}^m\left[\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j^{(i)}\right]\end{array}$$
根据梯度下降算法公式，迭代公式为：
$${\theta }_j:={\theta }_j+\alpha \frac{1}{m}\left[\left(y^{(i)}-h_{\theta }(x^{(i)})\right)x_j^{(i)}\right]$$
上面的$:=$符号表示先算右边的式子，算完后赋值给左边的变量。注意：左边和右边的${\theta }_i$值并不相等，右边是迭代前的${\theta }_i$值，左边的迭代后${\theta }_i$的值。

python代码实现

• 导入必要包

import numpy as np
import statsmodels.api as sm
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing, make_regression

• 加载数据函数

def load_data(data_path):
    data = np.loadtxt(data_path,delimiter=',')
    n = data.shape[1]-1
    data_x = data[:,0:n]
    data_y = data[:,-1].reshape(-1,1)
    return data_x,data_y

• 特征标准化函数

def data_std(data_x):
    mu = np.average(data_x, axis=0)
    sigma = np.std(data_x, axis=0, ddof=1)
    data_x = (data_x-mu)/sigma
    return data_x, mu, sigma

• 特征标准化的必要性：当特征的尺度差异很大时，代价函数的等高线图可能是一个狭长的椭圆形。在这种情况下，如果使用未经标准化的数据，梯度下降可能需要很多迭代才能到达最小值点，因为更新步长会在不同维度上不均衡。标准化可以使得各特征具有相似的尺度，从而使梯度下降更快地收敛。
• 损失函数

def compute_loss(data_x, data_y, theta):
    row_num = data_x.shape[0]
    return np.sum(np.power(np.dot(data_x,theta)-data_y,2))/(2*row_num)

• 线性回归函数

def linear_reg(data_x, data_y, theta, alpha, steps):
    loss_list = []
    temp_ones = np.ones(data_x.shape[0]).transpose()
    data_x = np.insert(data_x, 0, values=temp_ones, axis=1)
    row_num, col_num = data_x.shape
    for step in tqdm(range(steps)):
        loss_list.append(compute_loss(data_x, data_y, theta))
        for i in range(col_num):
            theta[i] = theta[i]+(alpha/row_num)*(np.sum(data_y - np.dot(data_x, theta)*data_x[:,i].reshape(-1,1)))
    return theta, loss_list

• 关键行为：在$x$数据前添加全1列（即上文提到的$x_0=1$），作为常数项；更新权重参数。
• 函数调用

data_x, data_y = load_data('/kaggle/input/studyml/data1.txt')
data_x, mu, sigma = data_std(data_x)
# 初始化权重
theta = np.zeros(data_x.shape[1]+1).reshape(-1,1)
steps = 400
alpha = 0.0065
theta, loss = linear_reg(data_x, data_y, theta, alpha, steps)
print(theta)
# 打印结果：[[5.4091][5.4535]]

• 关键行为：特征标准化；全零初始化权重（注意要记得常数项）；设定学习率；设定迭代次数；打印最终权重参数。
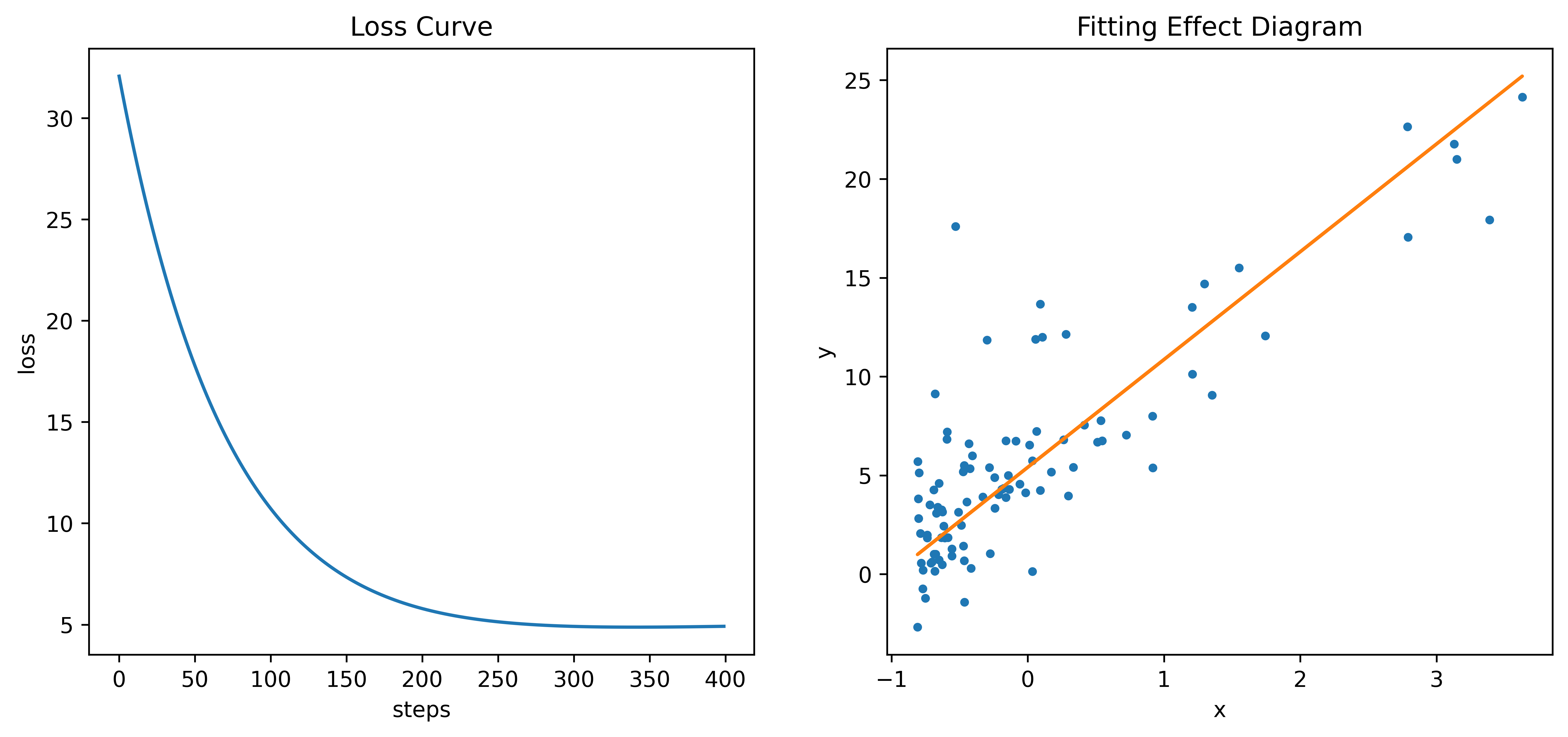
• 绘制Loss曲线（左）和拟合效果图（右）

plt.figure(figsize=(12,5),dpi=600)
plt.subplot(1,2,1)
plt.title("Loss Curve")
plt.xlabel("steps")
plt.ylabel("loss")
plt.plot(loss)
plt.subplot(1,2,2)
plt.plot(data_x, data_y, ".")
plt.plot(data_x, theta[0]+theta[1]*data_x)
plt.title("Fitting Effect Diagram")
plt.xlabel("x")
plt.ylabel("y")
plt.show()

梯度下降算法求解岭回归

岭回归在线性回归的基础上引入了L2正则化，用于惩罚大的回归系数。减轻了多重共线性和过拟合的影响，是一种更为稳健的回归技术，尤其适用于特征间存在高度相关性或特征数量大于样本数量的情况。

岭回归的目标函数变为：
$$\begin{array}{rl}J(\theta )& =\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)}-y^{(i)}\right)}^2+\lambda \Vert \theta {\Vert }_2^2\\ & =\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)}-y^{(i)}\right)}^2+\lambda \sum _{j=0}^n{\theta }_j^2\end{array}$$
目标函数对$\theta$的偏导数：
$$\begin{array}{rl}\frac{\partial }{\partial {\theta }_j}J(\theta )& =\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=0}^n{\theta }_j^2\\ & =\frac{1}{m}\sum _{i=1}^m\left[\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j^{(i)}\right]+2\lambda {\theta }_j\end{array}$$

根据梯度下降算法公式，迭代公式为：
$${\theta }_j:={\theta }_j+\alpha \frac{1}{m}\left[\left(y^{(i)}-h_{\theta }(x^{(i)})\right)x_j^{(i)}\right]-2\lambda {\theta }_j$$

python代码实现

• 岭回归函数

def ridge_reg(data_x, data_y, theta, alpha, steps, lamda=0.02):
    loss_list = []
    temp_ones = np.ones(data_x.shape[0]).transpose()
    data_x = np.insert(data_x, 0, values=temp_ones, axis=1)
    row_num, col_num = data_x.shape
    for step in tqdm(range(steps)):
        loss_list.append(compute_loss(data_x, data_y, theta))
        for i in range(col_num):
            theta[i] = theta[i]+(alpha/row_num)*(np.sum(data_y - np.dot(data_x, theta)*data_x[:,i].reshape(-1,1))) - 2*lamda*theta[i]
    return theta, loss_list

• 函数调用

data_x, data_y = load_data('/kaggle/input/studyml/data1.txt')
data_x, mu, sigma = data_std(data_x)
theta = np.zeros(data_x.shape[1]+1).reshape(-1,1)
steps = 400
alpha = 0.0065
theta, loss = ridge_reg(data_x, data_y, theta, alpha, steps, lamda=0.001)
print(theta)
# 打印结果：[[4.3183][4.3486]]

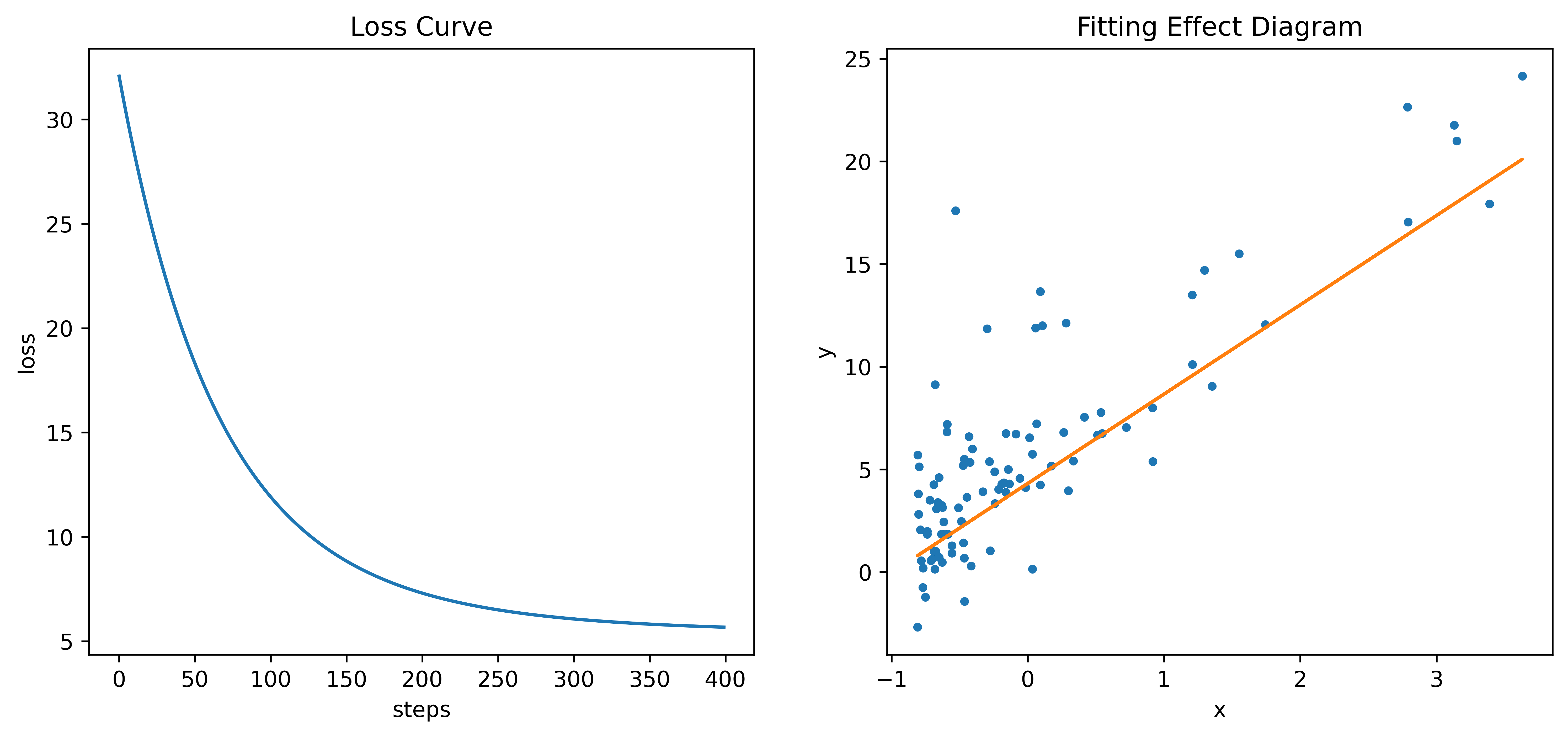
• 绘制Loss曲线（左）和拟合效果图（右）

plt.figure(figsize=(12,5),dpi=600)
plt.subplot(1,2,1)
plt.plot(loss)
plt.title("Loss Curve")
plt.xlabel("steps")
plt.ylabel("loss")
plt.subplot(1,2,2)
plt.plot(data_x, data_y, ".")
plt.plot(data_x, theta[0]+theta[1]*data_x)
plt.title("Fitting Effect Diagram")
plt.xlabel("x")
plt.ylabel("y")

梯度下降算法求解LASSON回归

Lasso回归使用L1正则化，在损失函数中添加了所有权重绝对值的和的惩罚项。可以将一些特征的权重精确地缩减到零。

LASSON回归目标函数变为：
$$\begin{array}{rl}J(\theta )& =\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)}-y^{(i)}\right)}^2+\lambda |\theta {|}_1\end{array}$$

在前面我们说过添加$\frac{1}{2m}$是为了数学上的便利，并非必要。即使没有前面的系数，目标函数仍然有效，因为优化算法（梯度下降）寻找的是目标函数的最小值点，而乘以一个正的常数并不改变函数的最小值位置。换句话说，无论目标函数乘以什么正的常数，最小化该目标函数所得到的参数$\theta$是相同的。为了数学表达式的简洁性，去掉前面的$\frac{1}{2m}$，因为括号平方里面的减数与被减数可以对调，再将$h_{\theta }$展开为一般式，得到了下面简化后的目标函数。

$$J(\theta )=\sum _{i=1}^m{\left(y^{(i)}-\sum _{j=0}^n{\theta }_j{x}_j^{(i)}\right)}^2+\lambda \sum _{j=0}^n|{\theta }_j|$$

先对加号前面的部分进行求导：

$$\begin{array}{rl}\frac{\partial }{\partial {\theta }_k}RSS(\theta )& =\frac{\partial }{\partial {\theta }_k}\sum _{i=1}^m{\left(y^{(i)}-\sum _{j=0}^n{\theta }_j{x}_j^{(i)}\right)}^2\\ & =2\sum _{i=1}^m\left(y^{(i)}-\sum _{j=0}^n{\theta }_j{x}_j^{(i)}\right)(-x_k^{(i)})\\ & =-2\sum _{i=1}^m\left(x_k^{(i)}{y}^{(i)}-x_k^{(i)}\sum _{j=0}^n{\theta }_j{x}_j^{(i)}\right)\\ & =-2\sum _{i=1}^m\left[x_k^{(i)}{y}^{(i)}-x_k^{(i)}\sum _{j=0,j\ne k}^n\left({\theta }_j{x}_j^{(i)}+{\theta }_k{x}_k^{(i)}\right)\right]\\ & =-2\sum _{i=1}^m\left[x_k^{(i)}{y}^{(i)}-\left(x_k^{(i)}\sum _{j=0,j\ne k}^n{\theta }_j{x}_j^{(i)}\right)-{\theta }_k{\left(x_k^{(i)}\right)}^2\right]\\ & =-2\sum _{i=1}^m\left[x_k^{(i)}\left(y^{(i)}-\sum _{j=0,j\ne k}^n{\theta }_j{x}_j^{(i)}\right)\right]+2{\theta }_k\sum _{i=1}^m\left(x_k^{(i)}\right)\end{array}$$
令：
$$\begin{array}{rl}{p}_k& =\sum _{i=1}^m\left[x_k^{(i)}\left(y^{(i)}-\sum _{j=0,j\ne k}^n{\theta }_j{x}_j^{(i)}\right)\right]\\ z_k& =\sum _{i=1}^m{\left(x_k^{(i)}\right)}^2\end{array}$$
则：
$$\frac{\partial }{\partial {\theta }_k}RSS(\theta )=-2p_k+2{\theta }_k{z}_k$$

现在对加号后面的L1正则化求偏导：

$$\frac{\partial }{\partial {\theta }_k}R(\theta )=\frac{\partial }{\partial {\theta }_k}\lambda \sum _{j=0}^n|{\theta }_j|=\{\begin{array}{ll}-\lambda & {\theta }_x<0\\ [-\lambda ,\lambda ]& {\theta }_k=0\\ \lambda & {\theta }_k>0\end{array}$$

则$J(\theta )$对$\theta$的偏导数为：
$$\frac{\partial }{\partial {\theta }_k}J(\theta )=-2p_k+2{\theta }_k{z}_k+\{\begin{array}{ll}-\lambda & {\theta }_x<0\\ [-\lambda ,\lambda ]& {\theta }_k=0\\ \lambda & {\theta }_k>0\end{array}$$

$$\frac{\partial }{\partial {\theta }_k}J(\theta )=\{\begin{array}{ll}-2p_k+2{\theta }_k{z}_k-\lambda & {\theta }_x<0\\ [-2p_k-\lambda ,-2p_k+\lambda ]& {\theta }_k=0\\ -2p_k+2{\theta }_k{z}_k+\lambda & {\theta }_k>0\end{array}$$

令：

$$\frac{\partial }{\partial {\theta }_k}J(\theta )=0$$

得：

$${\theta }_k=\{\begin{array}{ll}\frac{p_k+\frac{\lambda }{2}}{z_k}& p_k<-\frac{\lambda }{2}\\ 0& -\frac{\lambda }{2}\le p_k\le \frac{\lambda }{2}\\ \frac{p_k-\frac{\lambda }{2}}{z_k}& p_k>\frac{\lambda }{2}\end{array}$$

python代码实现

• LASSO回归

def lasso_reg(data_x, data_y, theta, alpha, steps, lamda=0.02):
    temp_ones = np.ones(data_x.shape[0]).transpose()
    data_x = np.insert(data_x, 0, values=temp_ones, axis=1)
    row_num, col_num = data_x.shape
    loss_list = []
    for step in range(steps):
        loss_list.append(compute_loss(data_x, data_y, theta))
        for k in range(col_num):
            z_k = np.sum(data_x[:,k]**2)
            p_k = 0
            for i in range(row_num):
                temp = np.sum([data_x[i,j]*theta[j] for j in range(col_num) if j != k])
                p_k = p_k + data_x[i,k] * (data_y[i] - temp)
            if p_k+(lamda/2) < 0:
                theta[k] = (p_k + (lamda/2))/z_k
            elif p_k-(lamda/2) > 0:
                theta[k] = (p_k - (lamda/2))/z_k
            else:
                theta[k] = 0
    return theta, loss_list

• 函数调用

data_x, data_y = load_data('/kaggle/input/studyml/data1.txt')
data_x, mu, sigma = data_std(data_x)
# 变成列向量
theta = np.zeros(data_x.shape[1]+1).reshape(-1,1)
steps = 20
alpha = 0.0001
theta, loss = lasso_reg(data_x, data_y, theta, alpha, steps, lamda=0.02)
print(theta)
# 打印结果：[[5.8390, 4.6167]]

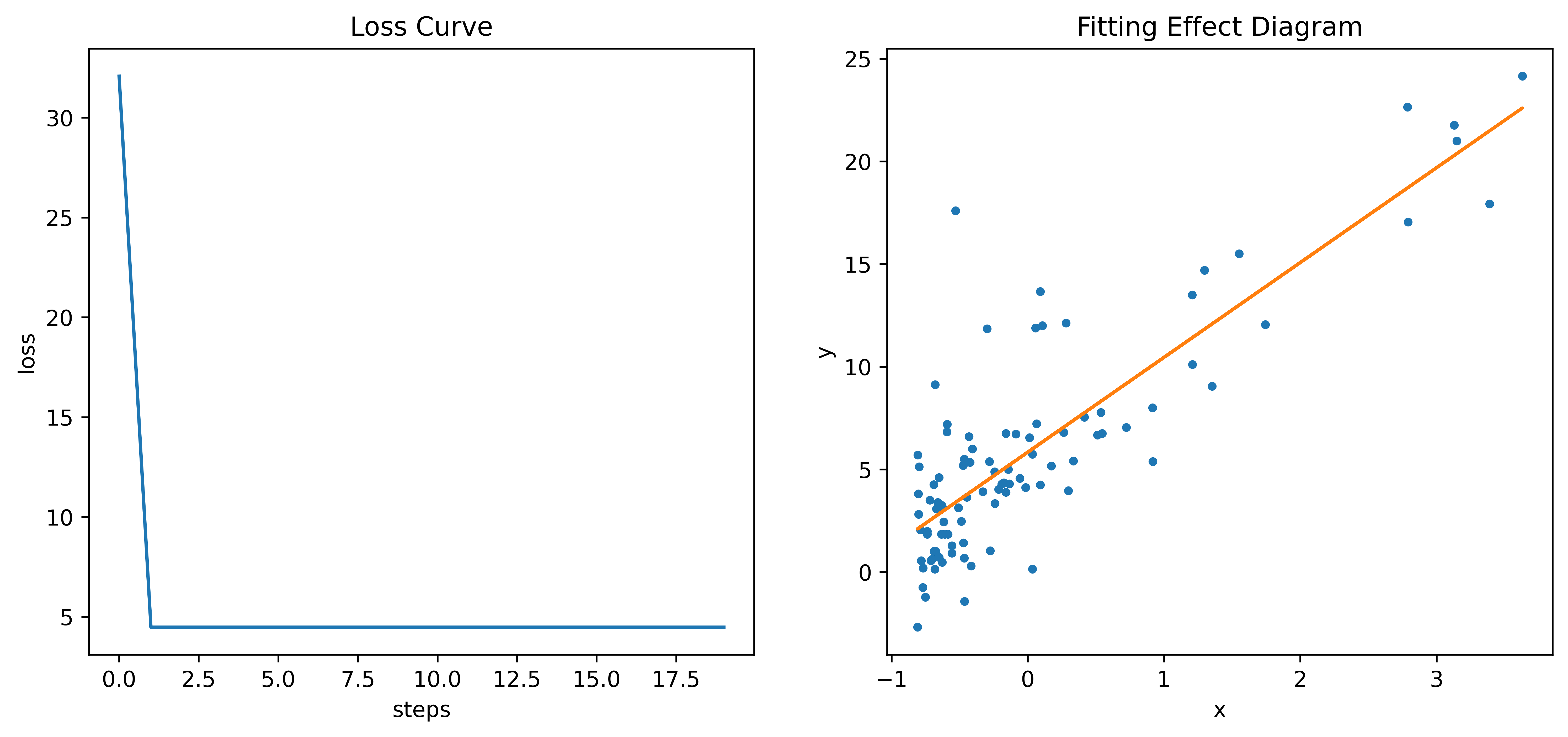
• 绘制Loss曲线（左）和拟合效果图（右）

plt.figure(figsize=(12,5),dpi=600)
plt.subplot(1,2,1)
plt.plot(loss)
plt.title("Loss Curve")
plt.xlabel("steps")
plt.ylabel("loss")
plt.subplot(1,2,2)
plt.plot(data_x, data_y, ".")
plt.plot(data_x, theta[0]+theta[1]*data_x)
plt.title("Fitting Effect Diagram")
plt.xlabel("x")
plt.ylabel("y")

岭回归和LASSON回归对比

• 岭回归：
  • 岭回归使用L2正则化，即在损失函数中添加了所有权重的平方和的惩罚项。
  • 这意味着如果一个权重很大，它的平方会更大，从而对损失函数的贡献也更大，导致优化过程倾向于选择较小的权重值。
  • 岭回归可以减少权重的大小，但不会将它们精确地缩减到零，这意味着所有特征都会被保留，只是其影响可能被减弱。
  • 岭回归有助于处理多重共线性（当自变量之间存在强相关性时）的问题，因为它会平均分配这些变量的影响。
• LASSON回归：
  • Lasso回归使用L1正则化，即在损失函数中添加了所有权重绝对值的和的惩罚项。
  • 由于L1正则化是基于绝对值，它有“稀疏化”效应，意味着它可以将一些特征的权重精确地缩减到零，从而实现特征选择。
  • Lasso回归能够识别并消除不重要的特征，这在高维数据集中尤其有用，因为它可以帮助模型专注于最相关的特征。
  • 当特征数量大于样本数量时，Lasso回归仍然可以给出有意义的结果，而岭回归则可能表现不佳。

总结来说，如果你关心的是特征选择并且想要简化模型，Lasso回归可能是更好的选择。如果你更关心处理多重共线性和保持所有特征的信息，那么岭回归可能更适合。在实践中，通常会通过交叉验证来调整正则化参数，并根据具体任务的需求来选择合适的回归方法。

最小二乘法

最小二乘法是一种统计学方法，用于通过最小化误差平方和来找到数据的最佳函数匹配。最小二乘法的目标函数为：
$$\begin{array}{rl}J(\theta )& =\frac{1}{2}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2\end{array}$$

写成矩阵相乘的形式为：
$$\begin{gathered} J(\theta )=\frac{1}{2}(X\theta -y{)}^T(X\theta -y) \\ (ab{)}^T=b^T{a}^T\Rightarrow (X\theta -y{)}^T=({\theta }^T{X}^T-y^T) \\ J(\theta )=\frac{1}{2}({\theta }^T{X}^T-y^T)(X\theta -y) \\ J(\theta )=\frac{1}{2}({\theta }^T{X}^{T}X\theta -{\theta }^T{X}^{T}y-y^{T}X\theta +y^{T}y) \end{gathered}$$
则$J(\theta )$对$\theta$的偏导为：
$$\begin{gathered} {\nabla }_{\theta }J(\theta )=\frac{1}{2}\times \frac{\partial }{\partial \theta }\left[({\theta }^T{X}^{T}X\theta -{\theta }^T{X}^{T}y-y^{T}X\theta +y^{T}y)\right] \\ \frac{\partial (x^{T}Ax)}{\partial x}=2Ax\Rightarrow \frac{\partial ({\theta }^T{X}^{T}X\theta )}{\partial \theta }=2X^{T}X\theta \\ \frac{\partial (x^{T}A)}{\partial x}=A\Rightarrow \frac{\partial ({\theta }^T{X}^{T}y)}{\partial \theta }=X^{T}y \\ \frac{\partial (Ax)}{\partial x}=A^T\Rightarrow \frac{\partial (y^{T}X\theta )}{\partial \theta }=(y^{T}X{)}^T \\ {\nabla }_{\theta }J(\theta )=\frac{1}{2}(2X^{T}X\theta -X^{T}y-(y^{T}X{)}^T)=X^{T}X\theta -X^{T}y \end{gathered}$$
令：
$$\begin{gathered} {\nabla }_{\theta }J(\theta )=0 \\ {X}^{T}X\theta -X^{T}y=0 \\ {A}^{-1}A=1\Rightarrow (X^{T}X{)}^{-1}{X}^{T}X\theta =(X^{T}X{)}^{-1}{X}^{T}y \\ \theta =(X^{T}X{)}^{-1}{X}^{T}y \end{gathered}$$

python代码实现

• 最小二乘法

def least_squares(data_x, data_y):
    temp_ones = np.ones(data_x.shape[0]).transpose()
    data_x = np.insert(data_x, 0, values=temp_ones, axis=1)
    theta = np.linalg.inv(data_x.T.dot(data_x)).dot(data_x.T).dot(data_y)
    return theta

• 调用函数

data_x, data_y = load_data('/kaggle/input/studyml/data1.txt')
data_x, mu, sigma = data_std(data_x)
theta = least_squares(data_x, data_y)
print(theta)
# 打印结果：[[5.8391],[4.6169]]

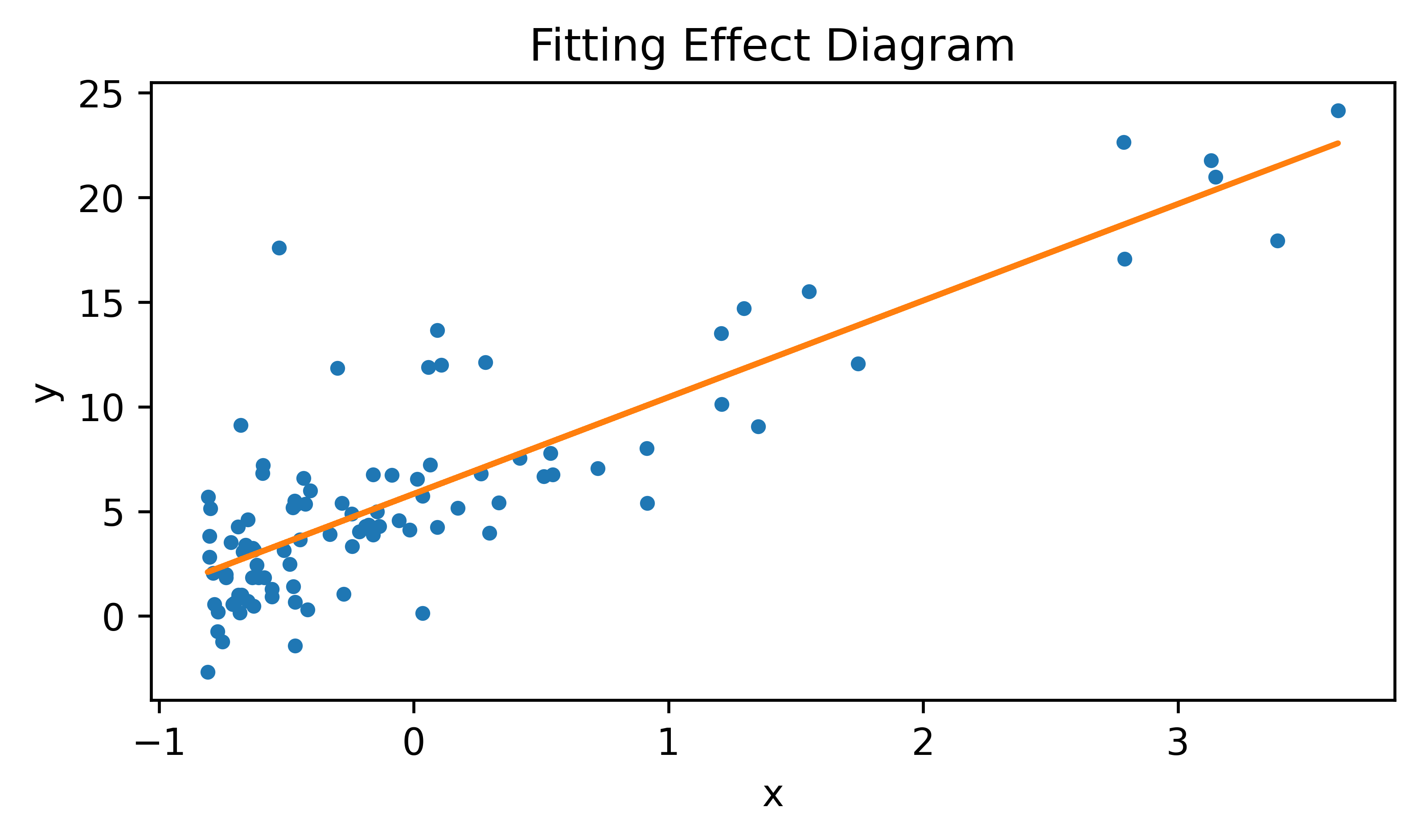
• 绘制拟合效果图

plt.figure(figsize=(6,3),dpi=600)
plt.plot(data_x, data_y, ".")
plt.plot(data_x, theta[0]+theta[1]*data_x)
plt.title("Fitting Effect Diagram")
plt.xlabel("x")
plt.ylabel("y")

• 使用statsmodels库验证结果

sm_x = sm.add_constant(data_x)
reg = sm.OLS(data_y, sm_x).fit()
print(reg.summary())

输出：

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.702
Model:                            OLS   Adj. R-squared:                  0.699
Method:                 Least Squares   F-statistic:                     223.8
Date:                Thu, 18 Jul 2024   Prob (F-statistic):           1.02e-26
Time:                        03:51:01   Log-Likelihood:                -243.95
No. Observations:                  97   AIC:                             491.9
Df Residuals:                      95   BIC:                             497.1
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          5.8391      0.307     19.020      0.000       5.230       6.449
x1             4.6169      0.309     14.961      0.000       4.004       5.230
==============================================================================
Omnibus:                       39.986   Durbin-Watson:                   0.994
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              108.142
Skew:                           1.455   Prob(JB):                     3.29e-24
Kurtosis:                       7.276   Cond. No.                         1.01
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.