R语言用极大似然和梯度下降算法估计GARCH(p)过程

 全文代码数据

 

最近我们被客户要求撰写关于GARCH的研究报告，包括一些图形和统计输出。

相关视频：时间序列分析：ARIMA GARCH模型分析股票价格数据

时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据

本文考虑一些ARCH(p)过程，例如ARCH(1)。

其中

有一个高斯白噪声 .

> for(t in 3:n){
+ sigma2[t]=w+a1*epsilon[t-1]^2+a2*epsilon[t-2]^2
+ epsilon[t]=eta[t]*sqrt(sigma2[t])
+ }

(红线是条件方差过程）。

> acf(epsilon,lag=50,lwd=2)

如果是一个ARCH()，那么就是一个AR(1)过程。所以第一个想法是考虑回归，就像我们对AR(1)所做的那样

> summary(lm(Y~X1,data=db))

 这里有一些明显的自相关。但由于我们的向量不能被认为是高斯分布的，使用最小二乘法也许不是最好的策略。实际上，如果我们的序列不是高斯分布的，它仍然是有条件的高斯分布的，因为我们假设是高斯（强）白噪声。

然后，似然函数是

而对数似然函数为

而一个自然的想法是定义

代码简单地说就是

> OPT=optim(par=
+ coefficients(lm(Y~X1,data=db)),fn=loglik)

由于参数必须是正数，我们在此假定它们可以写成一些实数的指数。观察一下，这些值更接近于用来生成我们的时间序列的值。

如果我们使用R函数来估计这些参数，我们会得到

> summary(garch(epsilon,c(0,1)))
...

 所以的置信区间是 

coef[2,1]+
+ c(-1.96,1.96)*coef[2,2]

 实际上，由于我们的主要兴趣是这个参数，所以有可能使用轮廓似然方法。

> OPT=optimize(function(x) -proflik(x), interval=c(0,2))
objective-qchisq(.95,df=1)
> abline(h=t,col="red")

当然，所有这些技术都可以扩展到高阶ARCH过程。例如，如果我们假设有一个ARCH(2)时间序列

其中

有一个高斯（强）白噪声 .对数似然性仍然是

而我们可以定义

上面的代码可以被修改，以考虑到这个额外的部分。

optim(par=
+ coefficients(lm(Y~X1+X2,data=db)),fn=loglik)

我们也可以考虑一些广义的ARCH过程，例如GARCH(1,1)。

其中

同样，可以使用最大似然技术。实际上，我们也可以用Fisher-Scoring算法编码，因为（在一个非常普遍的情况下 

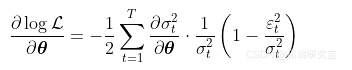
这里 . 使用标准的梯度下降算法，我们可以得到以下对GARCH过程的估计。

> while(sum(G^2)>1e-12){
+ s2=rep(theta[1],n)
+ for (i in 2:n){s2[i]=theta[1]+theta[2]*X[(i-1)]^2+theta[3]*s2[(i-1)]}

这里有趣的一点是，我们也得出了（渐进的）方差

>sqrt(diag(solve(H))

---