前言
这篇文章所讲解的所有内容都是基于红黑树的特性展开,也就是主要讲解如何利用红黑树的特性来实现一棵树的节点增加,而不是讲解红黑树的特性是怎么来的,加上科学家花几年时间研究出来的东西,总不能是我一篇小小文章可以讲解清楚的,希望读者可以理清自己的学习目的,即如何利用红黑树的特性来编写一棵树的增删改查。
为了缓解阅读批量,红黑树的增删分为上下部分,第一部分为本章——插入操作,删除操作有兴趣的读者可以自行去看下一章节。
1.红黑树的特性
既然是基于红黑树的特性展开,那我们肯定得先了解红黑树有什么特性:
- 所有节点都是红色或者黑色
- 根节点为黑色
- 所有的 NULL 叶子节点都是黑色
- 如果该节点是红色的,那么该节点的子节点一定都是黑色
- 所有的 NULL 节点到根节点的路径上的黑色节点数量一定是相同的
这些特性通过推导,可以得出 2 个结论:
- 从第 4 点可以得知,如果当前节点是红色,那他的父节点以及子节点肯定为黑色,因为红色节点的子节点为黑色,那他父节点是红色的话,当前节点也不可能是红色,即不会出现连续两个红色节点。
- 从第 5 点可以得知,我们对一棵树进行增删的时候,只要保证局部子树的黑色节点数量不变,同时符合红黑树的性质,那对整棵红黑树而言是没有任何影响的。
从上面推导的第 2 个结论可以知道,我们在对一棵红黑树进行增删的时候如果导致这棵树不符合红黑树的特性,那么我们应该是从局部开始想办法,如何保证通过变化局部的子树且不影响黑色节点的数量来达到恢复的效果,而不是直接从整棵红黑树开始解决问题,如果一直扩展到根节点前都无法调整,则可以考虑通过变色来减少/增加根节点其中一边的黑色节点。
接下来我们看个插入例子:

首先我们以插入节点 ( 下面称为 N ) 的父节点 ( 下面称为 P ) 为当前局部树的根节点;
可以看出,该节点和插入的新节点都为红色,不符合红黑树的特性,且无法通过变色和旋转达到局部平衡(变色会导致这个局部树的黑色节点增多,我们在调整局部树的时候,不能增加或减少当前局部树的黑色节点,除非局部树的根节点是整棵红黑树的根节点);
因此我们将 P 节点的父节点 ( 下面称为 G )当作局部树的根节点,可以看到,此时我们只需要基于 G 节点右旋,在将 P 节点变为黑色,便可以达到局部的平衡,此时整棵树也没有打破红黑树的特性。

可以看到,先前 G 为根节点的局部树经过调整后,符合了红黑树的特性,并且局部的黑色节点没有增加或减少,因此调整完成,无需将局部树进一步扩展。
一句话总结:
从局部进行变色和旋转进行调整,如果无法调整则扩展局部树范围,直到局部树的范围是整棵红黑树为止。
了解完调整红黑树的入口思路后,接下来,让我们正式进入编码环节。
2.定义红黑树结构
颜色枚举类:
public enum Color {
RED,BLACK;
}
红黑树节点类:
public class RBN {
//节点颜色
Color color;
//节点值,这里是用基本的int作为展示,如果是要自定义值的类型
//则需要该类实现比较的方法
int value;
//左孩子
RBN left;
//右孩子
RBN right;
//父母节点
RBN parent;
//构造函数,传入对应的值,默认颜色为红色
public RBN(int value){
this.color = Color.RED;
this.value = value;
}
//方便后期打印
@Override
public String toString() {
String color = this.color == Color.RED?"R":"B";
return color + value;
}
//设置左孩子的时候,需要将左孩子的父节点设置为当前节点
public void setLeft(RBN left){
this.left = left;
if(left != null){
left.parent = this;
}
}
public void setRight(RBN right){
this.right = right;
if(right != null){
right.parent = this;
}
}
}
红黑树类:
public class RBT {
//红黑树的根节点
RBN root;
//设置根节点需要将当前节点颜色变为黑色
//且切断当前节点与父节点的联系
public void setRoot(RBN node){
if(node == null){
root = null;
return;
}
node.color = Color.BLACK;
node.parent = null;
root = node;
}
//右旋,参数为旋转的基点
private void turnRight(RBN node){...}
//左旋,参数为旋转的基点
private void turnLeft(RBN node){...}
//新增节点入口
public void insert(int value){...}
//新增节点并修复树的代码方法
private insertNode(RBN parentNode,RBN newNode){...}
//删除节点入口
public RBN delete(int value){...}
//删除节点具体逻辑代码方法
private RBN deleteNode(RBN node){...}
//删除节点后红黑树的修复方法
private RBN fixForDelete(RBN node){...}
}
首先红黑树新增/删除后的调整主要是通过旋转和变色来恢复红黑树的特性,因此接下来我们先看看红黑树的旋转是如何实现。
2.1 旋转编码实现
首先,旋转的目的是为了平衡某个节点左右两侧黑色节点数量,例如右边的黑色节点比左边多一个,那么我们可以通过左旋的形式,在不修改右边黑色节点数量的同时,增加左边黑色节点的数量,达到该节点左右黑色子节点的数量一致,下面让我们一起看看具体的案例。
我们看看旋转的动图:
左旋:

右旋
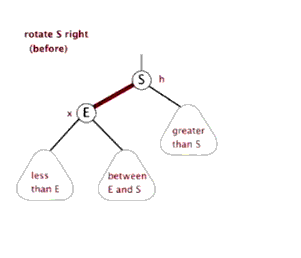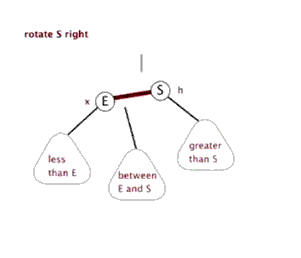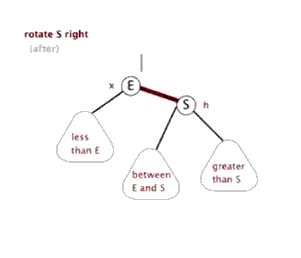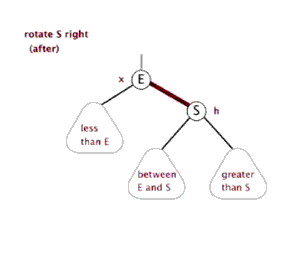
在左旋中,假如节点 E 是红色,节点 S 是黑色,那在旋转前,右边的黑色节点比左边的黑色节点多了一个,而旋转后,右边的黑色节点数量不变,但是左边的黑色节点增加了一个,达到了左右黑色节点数量的平衡。而右旋的场景,与左旋相反。
了解完旋转的目的,接下来我们正式进入旋转的编码:
左旋编码:
我们首先确定几个概念:
- 当前旋转基点称为 N 点,
- 当前旋转基点的父亲称为 P 点,
- 当前旋转基点的左孩子称为 L 点,
- 当前 L 点的右孩子称为 LR 点
通过上面动图可以看出,左旋的步骤如下:
- N 点的左孩子指向 LR 点
- L 点的右孩子指向 N 点
- P 点原先指向 N 点的孩子节点指向 L 点;如果 P 点为空,则将 L 点设置为根节点
由于在节点类的代码中我们设置当前节点左右孩子的同时修改了左右孩子的父节点指向,因此上述步骤在设置左右孩子节点后无需重新设置孩子节点的父节点指向
void turnLeft(RBN node){
RBN parent = node.parent;
RBN right = node.right;
RBN rightChild = right.left;
//步骤1
node.setRight(rightChild);
//步骤2
right.setLeft(node);
//步骤3
if(parent != null){
if(parent.value >= right.value){
parent.setLeft(right);
}else{
parent.setRight(right);
}
}else{
setRoot(right);
}
}
右旋编码:
右旋的操作只不过是和左旋的部分操作反过来,因此这里不在阐述右旋的步骤。
void turnRight(RBN node){
RBN parent = node.parent;
RBN left = node.left;
RBN leftChild = left.right;
node.setLeft(leftChild);
left.setRight(node);
if(parent != null){
if(parent.value >= left.value){
parent.setLeft(left);
}else{
parent.setRight(left);
}
}else{
setRoot(left);
}
}
完成红黑树的基础调整代码后,接下来便让我们直接看看红黑树的增删是如何利用旋转和变色达到恢复的效果。
3.红黑树的新增节点
我们先来看看新增节点的一个步骤:
- 寻找新增节点插入的位置
- 节点插入后,从插入节点的父节点作为局部树的根节点开始查看是否满足红黑树的特性
2.1. 满足特性,直接返回
2.2. 不满足特性,采用旋转和变色进行调整,如果当前局部树无法调整,将该局部树根节点的父节点作为新局部树的根节点进行调整,直到调整成功,满足特性。
3.1 第一个步骤,寻找插入的位置:
public void insert(int value){
RBN newNode = new RBN(value);
//根节点为空,直接设置当前节点为根节点即可
if(root == null || root == newNode){
setRoot(newNode);
return;
}
RBN parent = root;
//寻找符合条件的最底层父节点
//这里的逻辑和二叉树寻找位置的逻辑一样
while (true){
if(parent.value >= newNode.value){
//当前节点值比新增值大,说明新增节点在当前节点的左边
//如果当前节点的左节点为空,说明插入位置在当前节点的左边
if(parent.left == null)break;
//不为空说明这个节点没有位置可以插入
//则基于当前节点的左节点继续循环
parent = parent.left;
}else{
if(parent.right == null)break;
parent = parent.right;
}
}
//找到插入位置的父节点后,就可以进入下一个插入的具体步骤啦
this.insertNode(parent,newNode);
}
3.2 第二步骤,判断插入场景并选择调整方案
接下来我们来到步骤 2 ,步骤 2 中什么情况下插入是直接满足特性的呢?答案是父节点为黑色节点的时候,因为父节点为黑色节点,插入节点默认为红色节点,就算插入后,也不影响黑色节点的数量,所以插入后也还是满足红黑树的特性。这里同时也解释了为什么插入节点要默认为红色,核心就在于红色节点的插入不会影响黑色节点的数量。
因此下面我们探讨的场景,是父节点为红色节点的时候,由于插入节点也为红色,而连续的红色节点会破坏红黑树特性,因此需要考虑如何调整。
而这个时候单纯的以父节点为局部树的根节点是无法进行恢复调整,所以下面讨论这个场景的时候,我们会将该父节点的祖父节点作为局部树的根节点进行调整处理。
由于局部树的根节点变为插入节点的祖父节点,因此我们需要将插入节点的叔叔节点也纳入场景的分类当中。
我们先看一下,当父节点为红色的时候,插入一个红色节点会有多少种情况:
1. 叔叔节点为黑色
1.1 父亲节点是祖父节点的左孩子
- 假如插入节点在父亲节点的左侧,则这种场景我称之为 “UB-LL” 模式
( uncle black , parent In Left , newNode In Left)
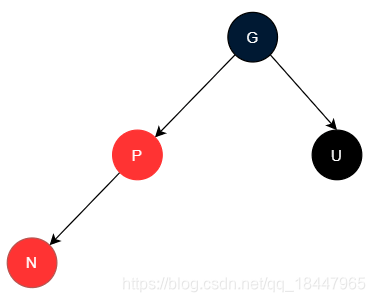
这个时候,我们只需要将父亲节点和祖父节点颜色交换,并基于祖父节点右旋,便完成了局部树的调整,如下图所示:

可以看到,调整后局部树的左右黑色节点数量和调整前一致,因此调整完成。
可能会有读者问假如叔叔节点不是NULL叶子节点,那上图不就不算调整成功吗?其实这里只要是父节点为红色,叔叔节点为黑色,那叔叔节点肯定是NULL叶子节点。因为父节点是被插入节点,同时是红色,那这个父节点肯定没有子节点;如果有,那只能是黑色节点,但如果是黑色节点,局部来看父节点的左右黑色数量就不一致了,所以父节点没有子节点;
同时为了保证插入前的树符合红黑树特性,叔叔节点只能是一个NULL叶子节点,不然祖父节点的左右黑色节点数量不一致。
因此我们在做插入的时候,一定要想着插入前是符合红黑树特性的,通过这种想法来使得我们后续操作的时候无需考虑太多,例如这里就不需要判断叔叔节点有没有子节点,只要他是黑色就行了。
- 假如插入节点在父亲节点的右侧,则这种场景我称之为 “UB-LR” 模式

这个场景我们可以通过将其转换为 “UB-LL” 模式,再利用"UB-LL" 模式的调整方式进行调整来完成恢复。我们基于父节点进行左旋,可以变为 “UB-LL” 模式,再将 P 节点当作新插入的节点,而 N 节点当作新插入节点的父节点进行方法递归便可以完成调整。下图为将 “UB-LR” 模式转换为 “UB-LL” 模式示意图:

完成转型后,后续操作则参考 “UB-LL” 模式的调整方案。
1.2 父亲节点是祖父节点的右孩子
- 假如插入节点在父节点的右侧,这种场景我称其为 “UB-RR” 模式
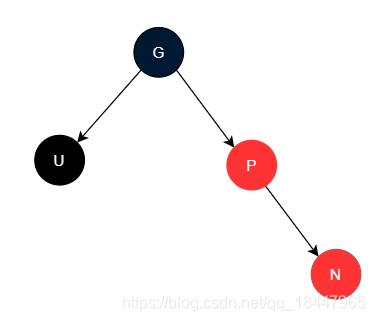
这个时候,我们调整的方式和 “UB-LL” 的调整方式反过来即可,即将祖父节点和父节点的颜色交换,再基于祖父节点左旋便可完成调整。

- 假如插入节点在父节点的左侧,这种场景我称其为 “UB-RL” 模式
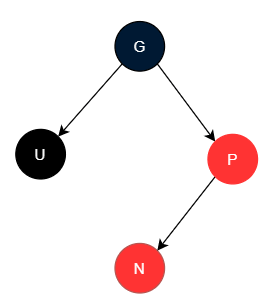
同理,我们可以将 "UB-RL"模式转换为"UB-RR"模式,再利用 "UB-RR"模式的调整方法进行调整即可恢复红黑树的特性。我们只要基于父节点进行右旋,便可转换为"UB-RR"模式,然后将父节点作为新插入的节点,将新插入的节点作为父节点进行方法递归。下图为将 "UB-RL"模式转换为"UB-RR"模式示意图:

后续操作则参考"UB-RR"模式的调整方式进行调整。
2. 叔叔节点为红色
这种场景下,祖父节点为黑色,同时有两个红色子节点,那我们插入一个新的节点时,只需要将父节点和叔叔节点变为黑色,祖父节点变为红色,那么以祖父节点为局部根节点来看,这就是一棵符合特性的红黑树(同时黑色节点数量没有变化)。
但是由于祖父节点变为红色,有可能与祖父节点的父节点发生冲突(连续红色),这个时候我们只需要将祖父节点作为一个新插入的节点,祖父节点的父节点作为父节点放入方法进行递归操作,便可完成调整。
所以叔叔节点为红色的情况下,无需考虑什么 “LL”、“LR”、“RR”、"RL"等情况。
接下来我们看个在这个场景下的插入例子:

将父亲节点和叔叔节点变为黑色,然后祖父节点变为红色:

可以看到,变化前后黑色节点的数量都是一致的,左右子树都只有两个黑色节点(包括叶子节点),而现在剩下的问题就在于祖父节点变为红色后,会不会对整棵红黑树造成影响,这个时候的思路与扩大局部树的思路一致,将祖父节点当作新的插入节点,并把祖父节点的父节点当作局部树的根节点,然后进行递归处理,直到调整完成。
看完了场景分类,接下来我们来一个总结:
- 父节点为黑色,直接插入,无需调整
- 父节点为红色
2.1. 叔叔节点为黑色
判断是 “LL”、“LR”、“RL”、“RR"中的哪种类型,如果是"LR”、“RL"类型则通过旋转父节点转换为"LL”、"RR"的类型;如果是"LL、"RR"类型则进行父节点/祖父节点的变色以及基于祖父节点进行旋转实现调整
2.2. 叔叔节点为红色
直接修改父节点和叔叔节点的颜色为黑色,修改祖父节点颜色为红色,将祖父节点当作插入节点进行递归调整。
private void insertNode(RBN parent,RBN newNode){
//场景1,父节点为黑色,直接插入
if(parent.color == Color.BLACK){
if(parent.value >= newNode.value){
parent.left = newNode;
}else{
parent.right = newNode;
}
newNode.parent = parent;
return;
}
//场景2,父节点为红色
//先判断是 LL / LR / RR / RL 中的哪一种插入类型
RBN grandparent = parent.parent;
RBN uncle = grandparent.value >= parent.value?
grandparent.right:grandparent.left;
String mode = (grandparent.value >= parent.value?"L":"R");
//将新节点插入到父节点当中
//插入当中,如果两个值是相等的,默认插入到父节点右边
//至于为什么,读者可以思考下,插入到左边会怎么样
if(parent.value > newNode.value){
mode += "L";
parent.setLeft(newNode);
}else{
mode += "R";
parent.setRight(newNode);
}
//场景2.1,叔叔节点为黑色节点
//这里判断叶子节点同时也判断是黑色是为了防止叔叔节点为红色的场景时
//递归祖父节点导致出现问题
if(uncle == null || uncle.color == Color.BLACK){
switch (mode) {
case "LL":
//交换父节点和祖父节点的颜色,基于祖父节点右旋
parent.color = Color.BLACK;
grandparent.color = Color.RED;
turnRight(grandparent);
break;
case "LR":
//基于父节点左旋,转换为LL模式
turnLeft(parent);
insertNode(newNode, parent);
break;
case "RR":
//交换父节点和祖父节点颜色,基于祖父节点左旋
parent.color = Color.BLACK;
grandparent.color = Color.RED;
turnLeft(grandparent);
break;
case "RL":
//基于父节点右旋,转换为RR模式
turnRight(parent);
insertNode(newNode, parent);
break;
}
}else{
//场景2.2,叔叔为红色节点
parent.color = Color.BLACK;
uncle.color = Color.BLACK;
//如果祖父节点是根节点,直接退出
//因为祖父节点都是根节点了,叔叔节点和父节点变为黑色
//相当于整棵树的路径都增加了一个黑色节点,整体已经平衡了
if(root == grandparent){
return;
}
//祖父节点还有父节点的话,将祖父节点变为红色
//当作新插入的节点进行递归
grandparent.color = Color.RED;
insertNode(grandparent.parent, grandparent);
}
}
3.3 新增总结
新增的核心在于保持局部树黑色节点数量的不变,除非局部树扩展到根节点,不然只要局部树没有扩展到根节点,那新增节点后根节点到叶子节点的不同路径的黑色节点数量是不会变的。
最后,附上一个打印树的工具方法,方便读者调试代码使用:
// 用于获得树的层数
public static int getTreeDepth(RBN root) {
return root == null ? 0 : (1 + Math.max(getTreeDepth(root.left), getTreeDepth(root.right)));
}
private static void writeArray(RBN currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
// 保证输入的树不为空
if (currNode == null) return;
// 先将当前节点保存到二维数组中
res[rowIndex][columnIndex] = currNode.toString();
// 计算当前位于树的第几层
int currLevel = ((rowIndex + 1) / 2);
// 若到了最后一层,则返回
if (currLevel == treeDepth) return;
// 计算当前行到下一行,每个元素之间的间隔(下一行的列索引与当前元素的列索引之间的间隔)
int gap = treeDepth - currLevel - 1;
// 对左儿子进行判断,若有左儿子,则记录相应的"/"与左儿子的值
if (currNode.left != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.left, rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
// 对右儿子进行判断,若有右儿子,则记录相应的"\"与右儿子的值
if (currNode.right != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.right, rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
public static void show(RBN root) {
if (root == null) System.out.println("EMPTY!");
// 得到树的深度
int treeDepth = getTreeDepth(root);
// 最后一行的宽度为2的(n - 1)次方乘3,再加1
// 作为整个二维数组的宽度
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
// 用一个字符串数组来存储每个位置应显示的元素
String[][] res = new String[arrayHeight][arrayWidth];
// 对数组进行初始化,默认为一个空格
for (int i = 0; i < arrayHeight; i ++) {
for (int j = 0; j < arrayWidth; j ++) {
res[i][j] = " ";
}
}
// 从根节点开始,递归处理整个树
// res[0][(arrayWidth + 1)/ 2] = (char)(root.val + '0');
writeArray(root, 0, arrayWidth/ 2, res, treeDepth);
// 此时,已经将所有需要显示的元素储存到了二维数组中,将其拼接并打印即可
for (String[] line: res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i ++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2: line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
























 1716
1716

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








