洛谷 P3385 【模板】负环

---

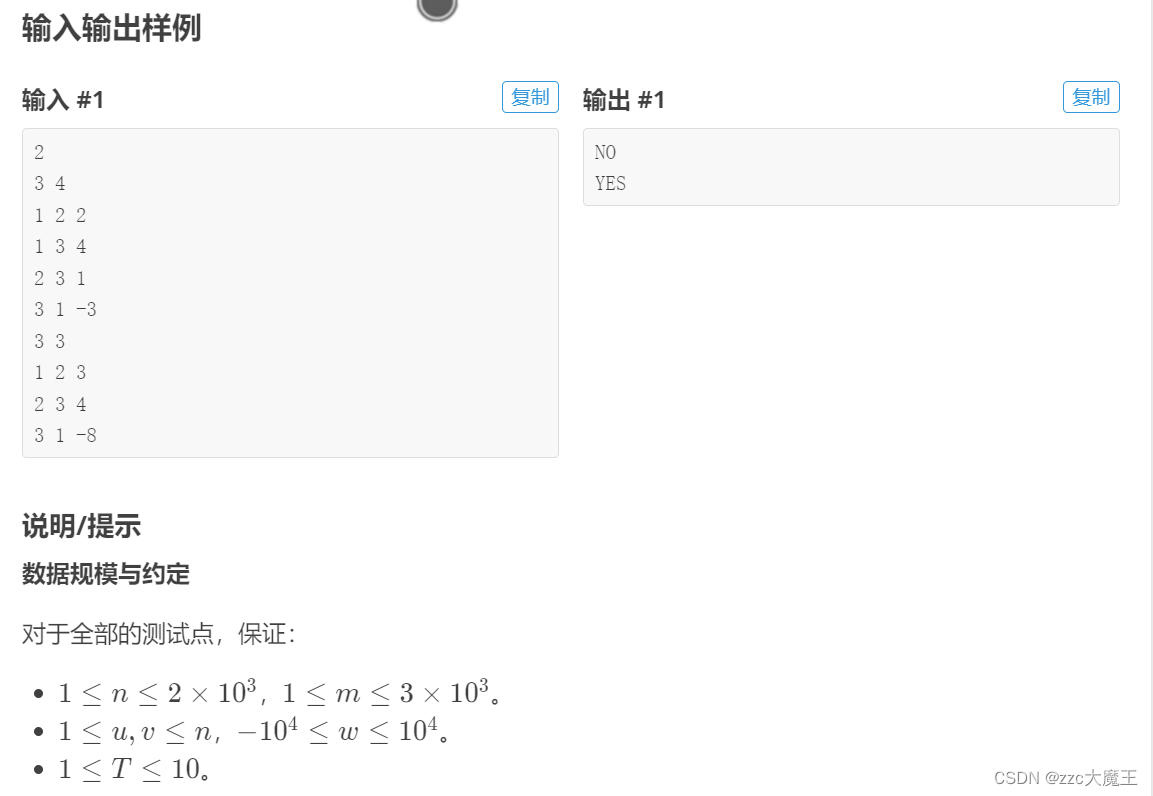
 这道题Dijkstra算法就没法来做了，因为出现负环会导致贪心策略出现错误，就好比完全背包和普通背包的遍历顺序是不一样的。

举一个反例，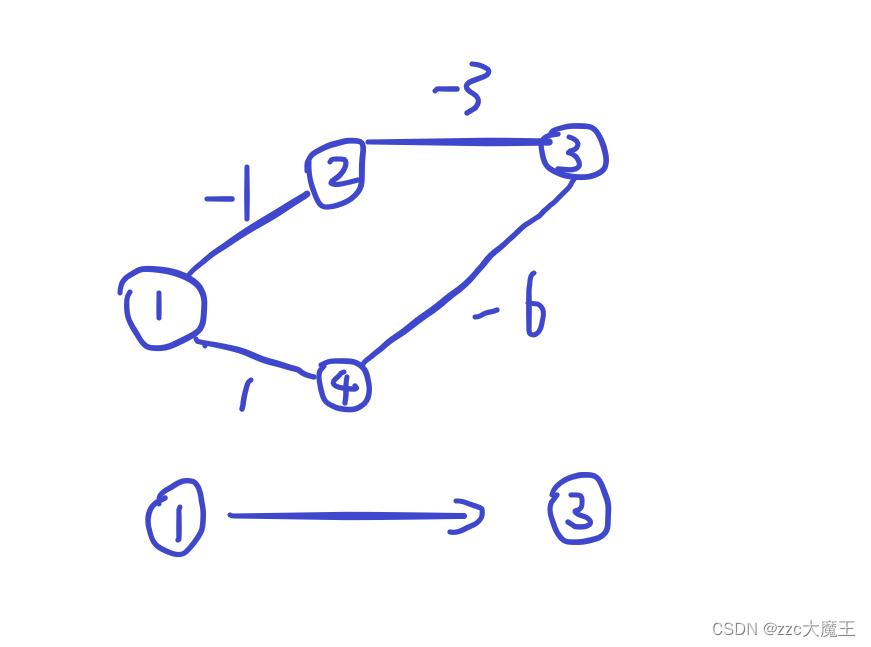

肉眼可见最短距离是-5，但是dj来执行，每次选最短的，①->②->③->④，永远走不出①->④->③这条路径。

具体一点来说Dijkstra可以看作是一个人拿着地图来走路，每走一次一次就记录一下最短距离，再回去找最短的那个接着走，每次都走最短的，那人走的路怎么会出现负数呢。

当然如果最后出现一条直线是负值或者其他情况就不能一概而论了，因为不会对最终结果产生影响。

例如

 

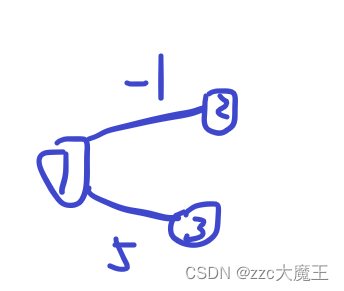
所以这道题就要引出spfa算法了，来看看两者的区别。

Dijkstra：
设置起点dist为0,其余为无穷大.
循环n次{
    1.在未经历的点中找出d