散列的含义
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
对不同的关键字可能得到同一散列地址,即k1≠k2,而f(k1)=f(k2),这种现象称为碰撞(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数f(k)和处理碰撞的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。
散列函数
(1)直接定址法
取关键字的某个线性函数为散列地址,Hash(Key)= Key 或 Hash(Key)= A*Key + B,A、B为常数。
(2)除数留余法
设散列表中允许的地址数为m,取一个不大于m,但接近或者等于m的质数p作为除数,按照哈希函数:Hash(key) = key mod p p<=m,将关键码转换成哈希地址。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
(3)平方取中法
平方后取中间的,每位包含信息比较多。假设关键字是1234,那么它的平方就是1522756,再抽取中间的3位就是227作为散列地址;再比如关键字是4321,那么它的平方就是18671041,抽取中间的3位就可以是671或者710用作散列地址。
(4)折叠法
有时关键码所含的位数很多,采用平方取中法计算太复杂,则可将关键码分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为散列地址,这方法称为折叠法。
比如:关键字是9876543210,散列表表长为三位,我们将它分成四组987|654|321|0|,然后将它们叠加求和987+654+321+0=1962,再求后3位得到散列地址为962。有时可能这还不能够保证分布均匀,不妨从一段向另一端来回折叠后对齐相加。比如将987和321反转,再与654和0相加,编程789+654+123+0=1566,此时的散列地址为566。
散列冲突
解决冲突的技术可以分为两类:开散列方法(open hashing,也称单链方法,separate chaining)和闭散列方法(closed hashing,也称开地址方法,open addressing)。开散列方法解决冲突是将冲突记录在表外,而闭散列方法是将冲突记录在表内的另一个空槽。
(1)开散列方法:运用单链表存储方式,不产生堆积现象,但因为附加了指针域而增加了空间开销。
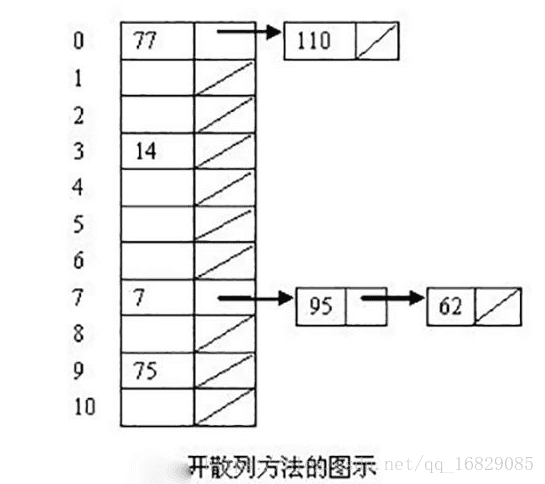
代码如下:
function HashTable()
{
this.table=new Array(137);
this.simpleHash=simpleHash;
this.betterHash=betterHash;
this.showDistro=showDistro;
this.put=put;
this.get=get;
this.buildChains=buildChains;//开链法
}
function put(key,data){
// let pos=this.simpleHash(key);
let pos=this.betterHash(key);
let index=0;
while(this.table[pos][index]!=undefined){
index++;
}
this.table[pos][index]=data;
}
function get(key){
// let pos=this.simpleHash(key);
let pos=this.betterHash(key);
let index=0;
if(this.table[pos][index]==key){
return this.table[pos][index];
}else{
while(this.table[pos][index]&&this.table[pos][index]!=key){
index++;
}
return this.table[pos][index];
}
}
//容易发生碰撞
function simpleHash(data){
let total=0;
for(let i=0;i<data.length;i++){
total +=data.charCodeAt(i);
}
return total%this.table.length;
}
//使用霍纳算法的散列函数
function betterHash(string){
const H=37;
let total=0;
for(let i=0;i<string.length;i++){
total +=H*total+string.charCodeAt(i);
}
total=total%this.table.length;
if (total<0) {
total +=this.table,length-1;
}
return parseInt(total);
}
function showDistro(){
let n=0;
for(let i=0;i<this.table.length;i++){
if (this.table[i][0] !=undefined) {
console.log(i+":"+this.table[i]);
}
}
}
//开链法
function buildChains(){
for(let i=0;i<this.table.length;i++){
this.table[i]=new Array();
}
}
//测试
let someNames=["David","Jennifer","Donnie","Raymond",
"Cynthia", "Mike", "Clayton", "Danny",
"Jonathan","Tom","Jack","Divad","Caylton"];
let hTable=new HashTable();
hTable.buildChains();
for(let i=0;i<someNames.length;i++){
hTable.put(someNames[i],someNames[i]);
}
hTable.showDistro();(2)闭散列方法:运用顺序表存储,存储效率较高,但容易产生堆积,查找不易实现,需要用到二次再查找。闭散列方法有桶式散列、线性探查、二次探查、双散列方法。
//线性探测法
function HashTable()
{
this.table=new Array(137);
this.values=[];
this.betterHash=betterHash;
this.showDistro=showDistro;
this.put=put;
this.get=get;
}
function put(key,data){
let pos=this.betterHash(key);
while(this.table[pos]!=undefined){
pos++;
}
this.table[pos]=key;
this.values[pos]=data;
}
function get(key){
let pos=this.betterHash(key);
if(this.table[pos]==key){
return this.values[pos];
}else{
while(this.table[pos]&&this.table[pos]!=key){
pos++;
}
return this.values[pos];
}
}
//使用霍纳算法的散列函数
function betterHash(string){
const H=37;
let total=0;
for(let i=0;i<string.length;i++){
total +=H*total+string.charCodeAt(i);
}
total=total%this.table.length;
if (total<0) {
total +=this.table,length-1;
}
return parseInt(total);
}
function showDistro(){
let n=0;
for(let i=0;i<this.table.length;i++){
if (this.table[i] !=undefined) {
console.log(i+":"+this.values[i]);
}
}
}
//测试
let someNames=["David","Jennifer","Donnie","Raymond",
"Cynthia", "Mike", "Clayton", "Danny",
"Jonathan","Tom","Jack","Divad","Caylton"];
let hTable=new HashTable();
for(let i=0;i<someNames.length;i++){
hTable.put(someNames[i],someNames[i]);
}
hTable.showDistro();
console.log(hTable.get('Town'));//undefined
console.log(hTable);







 本文详细介绍了散列表(哈希表)的概念与工作原理,包括散列函数的设计、常见的散列方法如直接定址法、除数留余法等,以及解决散列冲突的两种主要方法:开散列(单链法)和闭散列(开地址法)。通过具体的代码示例展示了如何实现散列表及其冲突解决机制。
本文详细介绍了散列表(哈希表)的概念与工作原理,包括散列函数的设计、常见的散列方法如直接定址法、除数留余法等,以及解决散列冲突的两种主要方法:开散列(单链法)和闭散列(开地址法)。通过具体的代码示例展示了如何实现散列表及其冲突解决机制。
















 831
831

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








