本文深入解析平衡二叉树的四种不平衡类型：LL、RR、LR、RL，并详细介绍了每种类型的调整策略，包括左旋和右旋操作，帮助读者理解和掌握平衡二叉树的自我调整机制。
这篇文章只讲了左旋右旋,书中的二叉树简单实现及中序前序后序遍历请查看下一篇文章
《大话数据结构》----二叉树----二叉树简单实现—插入中序前序后序遍历算法
二叉树
- 定义
二叉树(Binary) 是n(n>=0)个结点的有效集合,该集合或者为空集(称空二叉树),或者由一个根节点和两棵互不相交的/分别称为根节点的左子树和右子树的二叉树组成
- 特点
- 每个结点最多有两棵子树
- 左子树和右子树是有顺序的,次序不能任意颠倒
- 即使书中某节点只有一颗子树,也要区分它是左子树还是尊右子树
因为在做二叉树实现中初始化环节,涉及到左旋右旋等基本操作,要不然就是一个链表结构了 就会涉及后面的章节8.6(p314),不过早晚都要看的.
所以基本上这次就完成了一个平衡二叉树
平衡二叉树
平衡二叉树(Self-Balancing Binary Search Tree或 Height-Balanced Binary Search Tree),是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1
它是一种高度平衡的二叉树,要么它是一颗空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1
平衡因子
因为这个概念很重要,所以加了标题
将二叉树节点的左子树深度减去右子树深度的值称为平衡因子(Balance)
再加上上面平衡二叉树的性质,得出:
只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的.
附上Node对象
package ***;
/**
* @Author: wsh
*/
public class Node {
Node parent;
Node leftChild;
Node rightChild;
Integer val;
public Node(Node parent, Node leftChild, Node rightChild, Integer val) {
this.parent = parent;
this.leftChild = leftChild;
this.rightChild = rightChild;
this.val = val;
}
public Node(Integer val) {
this(null, null, null, val);
}
public Node(Node node, Integer val) {
this(node, null, null, val);
}
}
左旋右旋详解
最晦涩的左旋右旋 ,我在参考其他文章跳跃性都比较高.故在此拼接一下,顺便自己过一遍
首先建议查看平衡二叉树实现的实例1,目的就一个:LL型,RR型,LR型,RL型明白都是啥东西,啥样子.
(该文中没举例出LR型),因为四种类型避不开,必须要分情况讨论.
另外提醒重点看一下LL型和LR型,毕竟另外的两个差不多反个个(RR对应LL,RL对应LR),写的就相对粗一点
LL型调整
在<平衡二叉树(树的旋转)>1原理讲解中
（1）LL型调整：
由于在A的左孩子(L)的左子树(L)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1增至2。下面图1是LL型的最简单形式。显然，按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕结点B顺时针旋转一样。
在<java实现> 2的中,代码为
(这里的方法名应该是rightRotation,原文链接中为leftRotation,因为针对这种左左类型,要右旋)
这里说一下,下面段代码不能直接用,简单版,后续以此逐步升级,只是思路来处理右旋操作,因为没有考虑b和c的左右子节点,最终LL代码在此基础上稍作修改即可.
//此处aNode参数均为a节点,这里的示例图,只讲解遇到不平衡时咋办,这样遇到abc这种排列方式都可套用.
/**
a b
/ / \
b ===>>> c a
/
c
如果a不是根节点
情况1 abc旋转, b依然要在root的左侧
root root
/ \ / \
a N b N
/ ===>> / \
b c a
/
c
情况2
root root
/ \ / \
x a ====>> x b
/ \ / / \ / \
x x b x x c a
/
c
**/
/**
* 在这种情况，因为A和B节点均没有右孩子节点，
* 所以不用考虑太多,先实现代码
* @param aNode 代表A节点
*/
public Node leftRotation(Node aNode){
if(aNode != null){
Node bNode = aNode.leftChild;// 先用一个变量来存储B节点
bNode.parent = aNode.parent;// 重新分配A节点的父节点指向
//判断A节点的父节点是否存在
if(aNode.parent != null){// A节点不是根节点
/**
* 分两种情况
* 1、A节点位于其父节点左边，则B节点也要位于左边
* 2、A节点位于其父节点右边，则B节点也要位于右边
*/
if(aNode.parent.leftChild == aNode){
aNode.parent.leftChild = bNode;
}else{
aNode.parent.rightChild = bNode;
}
}else{// 说明A节点是根节点，直接将B节点置为根节点
this.root = bNode;
}
bNode.rightChild = aNode;// 将B节点的右孩子置为A节点
aNode.parent = bNode;// 将A节点的父节点置为B节点
return bNode;// 返回旋转的节点
}
return null;
}
看着好像很简单,然而,然而实际在代码中,
当新增一个z结点时,会破坏原有的平衡(z图中阴影地方,此时c为BL那个节点)
就要处理B还有右节点BR以及A是否为根节点及右节点(AR)
这样进行处理起来,就要多考虑一些
现在带上左右节点,结合步骤1,2,3,加上上面基础简单版代码完善一遍
LL型调整的一般形式如下图2所示，表示在A的左孩子B的左子树BL(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下：①将A的左孩子B提升为新的根结点；②将原来的根结点A降为B的右孩子；③各子树按大小关系连接(BL和AR不变，BR调整为A的左子树)。
真实场景处理的代码实现来自<java实现>3,在前几行多了几步操作左右子节点的内容
提前说一下 这里面的示例图,均为在新增后后后 打破平衡 打破平衡 打破平衡的demo
// 现实情况中 用符号实现如下,新增z时, a节点都会出现(3,1)的差2即平衡因子大于1的情况,要旋转
// 注意力放在a b c
(1)a为根节点
(3,1)a b
/ \ / \
(2,1)b x c a
/ \ ====>> / / \
(1,0)c y z y x
/
z
(2) 情况一,a在左节点
(3,2)root root
/ \ / \
(3,1)a x b x
/ \ /\ ===>> / \ / \
(2,1)b y x x c a x x
/ \ / / \
(1,0)c n z n y
/
z
(3)情况二 a在右节点
root (3,3) root
/ \ / \
x a(3,1) ====>> x b
/ \ / \ / \ / \
x x b(2,1) x x x c a
/ / \ / / / \
x c(1,0) n x z n x
/
z
过程同学有疑问: 以上都是节点b都有右节点n,若b没有右节点的话,会怎么样?
结论: 没有,原来就不平衡了,所以,应该先处理平衡二叉树,再处理新增z.就是这样的
root root root
/ \ / \ / \
a x b x b x
b无 / 先处理 / \ 平衡了,新增z / \ 这不就回到上面
右节点=>> b 右旋=>>> c a ===>> c a ===>>第一个例子么
/ / 那个(1)的情况.
c z
铛铛铛LL型代码环节
*/
//此处node参数对照图片中的A节点
public Node rightRotation(Node node){
if(node != null){
Node leftChild = node.leftChild;// 用变量存储node节点的左子节点
node.leftChild = leftChild.rightChild;// 将leftChild节点的右子节点赋值给node节点的左节点
if(leftChild.rightChild != null){// 如果leftChild的右节点存在，则需将该右节点的父节点指给node节点
leftChild.rightChild.parent = node;
}
leftChild.parent = node.parent;
// 即表明node节点为根节点
if(node.parent == null){
this.root = leftChild;
// 即node节点在它原父节点的右子树中
}else if(node.parent.rightChild == node){
node.parent.rightChild = leftChild;
}else if(node.parent.leftChild == node){
node.parent.leftChild = leftChild;
}
leftChild.rightChild = node;
node.parent = leftChild;
return leftChild;
}
return null;
}
放个栗子,对照一下看看效果
1 (3,1)1 2
/\ 新增6 / \ 失衡,右旋 / \
2 3 ====>> (2,1)2 3 ==========>> 4 1
/ \ /\ / /\
4 5 (1,0)4 5 6 5 3
/
6
RR型调整
由于在A的右孩子( R )的右子树 ( R )上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。图3是RR型的最简单形式。显然，按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕结点B逆时针旋转一样。
代码实现其实和LL型差不多,不过就是反了一下.
直接放最终版,中间的简单的代码 以及符号注释画图就略了,有需要可以评论,我再补
直接来看例子:
在原有0,1,2基础上插入3，是平衡的，再插入4，此时出现了不平衡，结点 1 和 2 的平衡因子都为 -2，结点2为最低不平衡结点，属于RR型,需左旋
对照代码看上面的图,基本上能在脑海中翻译过来
// node为a节点,上图中的2
public Node leftRotation(Node node){
if(node != null){
Node rightChild = node.rightChild;
node.rightChild = rightChild.leftChild;
if(rightChild.leftChild != null){
rightChild.leftChild.parent = node;
}
rightChild.parent = node.parent;
if(node.parent == null){
this.root = rightChild;
}else if(node.parent.rightChild == node){
node.parent.rightChild = rightChild;
}else if(node.parent.leftChild == node){
node.parent.leftChild = rightChild;
}
rightChild.leftChild = node;
node.parent = rightChild;
}
return null;
}
LR型调整
- 思路一: 我称为死记硬背型,因为根本找不到思路咋就…就转换完成了…
- 思路二: 左转+右转配合型,只要灵活搭配使用上面两个左右旋能解决
我觉得思路二好理解一些,接下来写第二个思路
思路一
记得东西比较多,但是按照文中①②③三步走即可完成
由于在A的左孩子(L)的右子树®上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1变为2。图5是LR型的最简单形式。显然，按照大小关系，结点C应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。
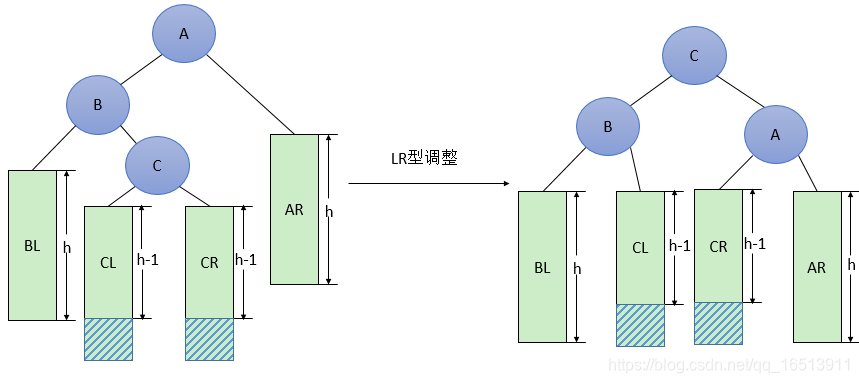
LR型调整的一般形式如下图所示，表示在A的左孩子B的右子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下：①将C的右孩子B提升为新的根结点；②将原来的根结点A降为C的右孩子；③各子树按大小关系连接(BL和AR不变，CL和CR分别调整为B的右子树和A的左子树)。
思路二: 左旋+右旋方式
在参考文章中写到
如果将C节点替换B节点位置，而B节点成为C节点的左节点，这样就成为了LL代码的那种情况
a a c
/ 以b左旋 / 以a右旋 / \
b ===>> c ====>> b a
\ /
c b
这么一波操作以后, 就能和思路一效果一样,其实思路一就是跳跃了一些…直接一步到位
跑题了,先说思路二中怎么针对以B结点左旋呢,然后再放进LL右旋.
- 先说针对B的左旋
显然,这里的"左旋"和RR型左旋操作略有不同
因为RR型操作的参数以A节点,而这里是以B节点.
那么,在代码上哪里不一样呢??? 就是判断参数是否根节点,在代码敲出来,差别就在于两行代码
//即判断当前节点是否为根节点.
if(node.parent == null){
this.root = rightChild;
}
这里为了初学方便理解把参数名换了一下, 其实还是RR型的代码
//
// bNode 代表B节点,
//但是!!! 其实和RR型一样,修改少了两句话,以及换了参数名
public Node rightBNodeRotation(Node bNode){
if(bNode != null){
// 用临时变量存储C节点
Node cNode = bNode.rightChild;
//处理c节点的左节点,如果有挂在b的右节点下.
bNode.rightChild = cNode.leftChild;
if (cNode.leftChild != null) {
cNode.leftChild.parent=bNode;
}
cNode.parent = bNode.parent;
// 这里因为bNode节点父节点存在，所以不需要判断。加判断也行,
if(bNode.parent.rightChild == bNode){
bNode.parent.rightChild = cNode;
}else{
bNode.parent.leftChild = cNode;
}
cNode.leftChild = bNode;
bNode.parent = cNode;
return cNode;
}
return null;
}
这么一波操作下来,就变成了LL型了(中间这个 a-c-b)
/**
a a c
/ 以b左旋 / 以a右旋 / \
b ===>> c ====>> b a
\ /
c b
**/
- 再解决LL型
中间这个很显然又回去LL型了,再套进去调用LL型,不过这次参数是a节点 - 最终,LR型就通过左旋+ 右旋 解决了
1 (3,1)1 (3,1)1 5
/ \ / \ / \ / \
2 3 ====>> (1,2)2 3 ======>>> (2,1)5 3 =====>>> 2 1
/ \ 5后插入6 / \ 1节点失衡 / 1节点失衡 / \ \
4 5 左右都行 4 5(1,0) 先左旋2,5 (1,1)2 右旋1,5,2 4 6 3
/ / \
6 4 6
RL型调整
RL型和LR型彼此彼此,这里还是两个思路
思路一,一步到位,细细琢磨步骤敲出来,
思路二,右旋+左旋方式,
- 引用内容为思路一
由于在A的右孩子®的左子树(L)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。下面是RL型的最简单形式。显然，按照大小关系，结点C应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。
RL型调整的一般形式如下图8所示，表示在A的右孩子B的左子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下：①将C的右孩子B提升为新的根结点；②将原来的根结点A降为C的左孩子；③各子树按大小关系连接(AL和BR不变，CL和CR分别调整为A的右子树和B的左子树)。
- 思路二: 针对RL这种类型,也可以通过两个旋转完成.
先上简单版本,看出思路先以b右旋,达到RR型,再以a左旋即可完成,
a a c
\ \ / \
b ===>> c =====>>> a b
/ \
c b
- 针对
b右旋
LR型我还写了一个针对b的左旋代码,其实就是RR型换了参数便于理解
这里的RL型,需要针对b的右旋代码就不写了,其实就是LL型代码 - 最后再套用RR型,左旋就好了.
收获
没有捷径,我一开始以为能绕过LLRR这些,发现翻来覆去只能一口口吃掉
放一张推算的草稿纸,我写这篇文章为了吸收和顺出来,一开始还需要在纸上画画
再往后面直接就在IDEA上敲符号了画图了.
因为学会了就能在脑海推算每一个步骤如何转换
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
