最大熵模型原理小结

　　最大熵模型（Maximum Entropy Model，MaxEnt）是一种很经典的分类算法，理解它有助于加深我们对逻辑回归、支持向量机、决策树等算法的理解。最大熵模型是将最大熵原理应用到分类任务得到的模型。在解释最大熵原理和最大熵模型之前，先简单对熵的概念进行一下回顾。

1. 信息熵，联合熵，条件熵

　　信息论的基本想法是发生一个不太可能发生的事件比发生一个非常可能发生的事件能提供更多的信息。比如说，“今天早上太阳升起”几乎一定会发生的，这句话包含的信息量很少；如果说“今天早上有日食”，日食是非常罕见的，那么这句话包含的信息量就很多了。一个事件$\mathrm{x}=x$包含的信息量称为自信息（Self-information），自信息也可以理解为事件发生之前的不确定性：

$$I(x)=-\log P(x)$$ 其中log以2为底时，$I(x)$的单位是比特或香农；log以$e$为底时，$I(x)$单位是奈特，为了计算方便，本文都是自然对数。
　　自信息只能处理单个的输出。我们可以用香农熵（也叫信息熵）来对整个概率分布中的不确定性总量进行量化： $$H(x)=\mathbb{E}_{x\sim P}[I(x)]=-\mathbb{E}_{x\sim P}[\log P(x)]\tag{1}$$ 对于离散变量 $$H(x)=-\mathbb{E}_{x\sim P}[\log P(x)]=-\sum_{i=1}^NP(x_i)\log P(x_i)\tag{2}$$ 换而言之，一个分布的信息熵是遵循这个分布的事件所产生信息总量的期望，即所有自信息的加权平均。信息熵满足下列不等式： $$0 \le H(P) \le \log|X|$$ 其中$|X|$是$X$取值的个数。那些接近确定的分布（输出几乎可以确定）具有较低的熵；那些接近均匀分布的概率具有较高的熵。当且仅当$X$的分布是均匀分布事上式右边的等号成立，所以$X$服从均匀分布时熵最大。
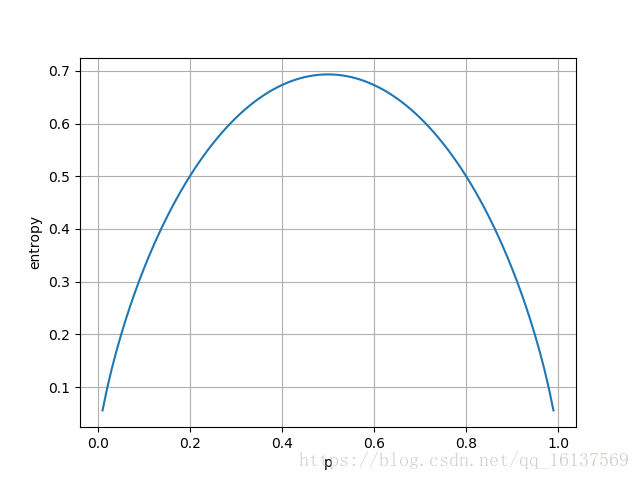
　　以二值随机变量为例，说明更接近确定性的分布是如何具有较低的信息熵。下图中$x$轴是$p$，表示二值随机变量等于1的概率，其信息熵由$-(p\log p + (1-p)\log(1-p))$给出。当$p$接近0或者1时，分布几乎是确定的，当$p=0.5$时，是一个均匀分布，熵达到最大值1。这正好符合$\ln 2=0.693$（二值变量只有2个取值）。

该部分测试代码如下：

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 1, 0.01)   # 这里就没额外考虑log的值域了，会有个warning
entropy = -1 * (x * np.log(x) + (1 - x) * np.log(1 - x))  # ∑ p(x)logp(x)

plt.plot(x, entropy)
plt.xlabel('p'), plt.ylabel('entropy')
plt.grid(), plt.show()

　　推广到多个变量的联合熵：

$$H(X,Y)=-\sum_{i=1}^NP(x_i,y_i)\log P(x_i,y_i)\tag{3}$$ 联合熵是是在联合自信息$I(X,Y)$的期望。
　　条件熵是已知随机变量$X$的条件下随机变量$Y$的不确定性： $$\begin{align*}H(Y|X)&=\sum_{x \in X}P(x)H(Y|X=x)\\&=-\sum_{x\in X}P(x)\sum_{y\in Y}P(y|x)\log P(y|x)\\&=-\sum_{x\in X}\sum_{y\in Y}P(x, y)\log P(y|x)\tag{4}\end{align*}$$

2. 最大熵原理

　　最大熵原理是概率模型学习的一个准则。最大熵原理认为，学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。如果有约束条件，最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
　　参考第1节，假设离散随机变量$X$的概率分布是$P(X)$，则其熵为：

$$H(x)=-\sum_{i=1}^NP(x_i)\log P(x_i)$$ 熵满足下列不等式： $$0 \le H(P) \le \log|X|$$ 当$X$服从均匀分布时，右边等号成立，熵最大。
　　直观上来说，最大熵原理认为要选择的概率模型首先必须满足已有的事实，即约束条件。在没有更多信息的情况下，那些不确定的部分都是“等可能”的。最大熵原理通过熵的最大化来表示等可能性。别看说的有点玄乎，其实这在我们生活中也经常见到：比如给你一个6个面的色子，很自然的我们会认为每个面出现的概率都是$\frac{1}{6}$。如果已经告诉你出现“1”的概率为$\frac{1}{2}$，那么我们一般推测剩下5个面出现的概率都是$\frac{1}{10}$。做出这样推测的潜在逻辑就是，对于一个事件，不作出任何主观假设（不引入不可信的先验信息）往往是最可信的。
　　最大熵的思想在其他地方其实也能见到，比如我们建模选择概率分布默认比较好的选择是正态分布。其一，我们想要建模的很多分布的真实情况是比较接近正态分布的（中心极限定理，这里不展开了）。其二，在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性，即正态分布是对模型加入的先验知识量最少的分布，这正是最大熵的思想。

3. 最大熵模型

　　上面讲到的最大熵原理是统计学习中的一般原理，如果将它应用到分类，就得到了最大熵模型。简单来说，最大熵模型做的事就是假设分类模型是一个条件概率分布$P(Y|X)$，然后利用最大熵原理选择最好的分类模型。
　　假设分类模型是一个条件概率分布$P(Y|X)$，$X\in \mathbb{R}^n$表示输入，$Y\in \mathbb{R}$表示输出。这个模型表示的是对于给定的输入$X$，以条件概率$P(Y|X)$输出$Y$。
　　给定数据集$T=\{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\}$，首先考虑模型应该满足的条件。给定训练集，就可以确定联合分布$P(X,Y)$的经验分布和边缘分布$P(X)$的经验分布，分别以$\tilde{P}(X,Y)$和$\tilde{P}(X)$表示：

$$\begin{align*}\tilde{P}(X,Y)&=\frac{v(X=x,Y=y)}{N}\\ \tilde{P}(X)&=\frac{v(X=x)}{N}\end{align*}$$ 其中$v(X=x,Y=y)$表示训练集中样本$(x,y)$出现的频数，$v(X=x)$表示训练集中输入$x$出现的频数，$N$表示训练集样本总数。
　　用特征函数$f(x,y)$描述输入$x$和输出$y$之间的关系： $$f(x,y)=\begin{cases}1,　　x和y满足某一事实\\0,　　else\end{cases}$$ 可以认为出现在训练集中的$(x_i,y_i)$，全部有$f(x_i,y_i)=1$，对于一个训练样本可以有多个特征函数。
　　特征函数$f(x,y)$关于经验分布$\tilde{P}(X,Y)$的期望用$E_{\tilde{P}}(f)$表示： $$E_{\tilde{P}}(f)=\sum_{x,y}\tilde{P}(x,y)f(x,y)\tag{5}$$ 特征函数$f(x,y)$关于模型$P(Y|X)$和经验分布$\tilde{P}(X)$的期望用$E_P(f)$表示： $$E_P(f)=\sum_{x,y}\tilde{P}(x)P(y|x)f(x,y)\tag{6}$$ 如果模型能够从训练集中学习，那么可以假设这两个期望值相等，即 $$E_{\tilde{P}}(f)=E_P(f)$$ 不知道对不对，我认为这个其实就是根据联合分布的经验分布$\tilde{P}(x,y)$去估计真实联合分布$P(x,y)$，根据贝叶斯概率公式： $$P(x,y)=P(x)P(y|x)$$ 其中$P(y|x)$是我们的模型假设，是需要求的东西，$P(x)$是$x$的边缘分布，但真实的边缘分布无从得知，所以这里用$\tilde{P}(x)$来近似$P(x)$，所以对于(6)式有： $$E_{\tilde{P}}(f)=\sum_{x,y}\tilde{P}(x,y)f(x,y)\approx \sum_{x,y}P(x,y)f(x,y)$$ 现在得到模型的约束条件（如果有$n$个特征函数，约束条件就有$n$个） $$\sum_{x,y}\tilde{P}(x,y)f(x,y)=\sum_{x,y}\tilde{P}(x)P(y|x)f(x,y)\tag{7}$$ 后，我们只要找到满足(7)的模型$P(y|x)$就大功告成。
　　但显然$P(y|x)$的选取不止一种，那么如何才能确定最优的模型呢？这时就要用到第2节的最大熵原理了。最大熵原理认为熵最大的模型是最好的模型，条件分布$P(Y|X)$对应的条件熵为 $$\begin{align*}H(Y|X)&=-\sum_{x,y}P(x,y)\log P(y|x)\\&\approx-\sum_{x,y}\tilde{P}(x)P(y|x)\log P(y|x) \tag{8}\end{align*}$$ 　　于是我们的目标转化为求使$H(Y|X)$最大时对应的$P(y|x)$，求得的$P(y|x)$称为最大熵模型。

4. 最大熵模型的学习

　　经过上面的分析，不难得知最大熵模型的学习其实就是一个约束最优化问题。
　　对于给定的训练集$T=\{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\}$以及特征函数$f_i(x,y),i=1,2,\dots,n$，最大熵模型的学习等价于约束最优化问题：

$$\begin{align*}\max_{P}&H(P)=-\sum_{x,y}\tilde{P}(x)P(y|x)\log P(y|x)\\ s.t.&E_P(f_i)=E_{\tilde{P}}(f_i),　i=1,2,\dots,n\\&\sum_yP(y|x)=1 \end{align*}$$ 可以改写为等价的求最小值问题： $$\begin{align*}\min_{P}&-H(P)=\sum_{x,y}\tilde{P}(x)P(y|x)\log P(y|x)\\ s.t.&E_P(f_i)-E_{\tilde{P}}(f_i)=0,　i=1,2,\dots,n\\&\sum_yP(y|x)=1 \end{align*}\tag{9}$$ 求解约束最优化问题(9)所得出的解，就是最大熵模型学习的解。下面给出具体推导。
　　按照惯例，引入拉格朗日乘子$w_0,w_1,\dots,w_n$，定义拉格朗日函数为： $$\begin{align*}L(P,w)&=-H(P)+w_0(1-\sum_yP(y|x))+\sum_{i=1}^nw_i(E_{\tilde{P}}(f_i)-E_P(f_i))\\&=\sum_{x,y}\tilde{P}(x)P(y|x)\log P(y|x)+w_0(1-\sum_yP(y|x))+\sum_{i=1}^n(\sum_{x,y}\tilde{P}(x,y)f_i(x,y)-\sum_{x,y}\tilde{P}(x)P(y|x)f_i(x,y))\tag{10}\end{align*}$$ 对偶问题是 $$\max_w\min_PL(P,w)\tag{11}$$ 首先求解对偶问题(11)内部的极小化问题，记 $$\Psi(w)=\min_PL(P,w)=L(P_w,w)$$ 同时将其解记为 $$P_w=\arg\min_PL(P,w)=P_w(y|x)$$ 　　求$L(P,w)$对$P(y|x)$的偏导数并令其等于0，有： $$\begin{align*}\frac{\partial L(P,w)}{\partial P(y|x)}&= \sum_{x,y}\tilde{P}(x)(\log P(y|x)+1)-\sum_yw_0-\sum_{x,y}(\tilde{P}(x)\sum_{i=1}^nw_if_i(x,y)) \\&=\sum_{x,y}\tilde{P}(x)(\log P(y|x)+1-w_0-\sum_{i=1}^nw_if_i(x,y))=0\end{align*}$$ 解得 $$P_w(y|x)=\exp({\sum_{i=1}^nw_if_i(x,y)+w_0-1})=\frac{\exp{(\sum_{i=1}^nw_if_i(x,y))}}{\exp(1-w_0)}\tag{12}$$ 又因为$\sum_yP(y|x)=1$，得 $$P_w(y|x)=\frac{\exp{(\sum_{i=1}^nw_if_i(x,y))}}{Z_w(x)}\tag{13}$$ 其中$Z_w$为规范化因子 $$Z_w(x)=\sum_y\exp(\sum_{i=1}^nw_if_i(x,y))\tag{14}$$ 这样就得到了$P(y|x)$和$w$之间的关系，将(13-14)反代回$\Psi(w)$，这样$\Psi(w)$就是全部用$w$表示了。接着对$\Psi(w)$求极大，就可以得到极大化时对应的$w$向量的取值$w^*$，代入(13-14)就能得到$P_w(y|x)$的最终结果。
　　由于$\Psi(w)$是连续可导的，所以对$\Psi(w)$求极大化有很多种方法，比如梯度下降、牛顿法、拟牛顿法都可以。最大熵模型求解还有一种专用的优化方法，叫做改进的迭代尺度法（Improved Iterative Scaling, IIS）。

5. 极大似然估计

　　这里先简单上个结论：最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计。至于证明日后再补上来，最近开始秋招实在有点忙。

6. 小结

　　最大熵模型在分类方法中算是比较优的模型，但是由于它的约束函数数目一般来说会随着样本量的增大而增大，导致样本量很大的时候，对偶函数的优化求解过程非常慢。
　　MaxEnt优点是可以灵活设置约束条件，通过约束条件的多少可以调节模型对未知数据的适应度和对已知数据的拟合度。缺点是约束函数数量和样本数目有关，导致迭代过程计算量巨大，实际应用比较难。