Leetcode-407. Trapping Rain Water II [C++][Java]

目录

一、题目描述

二、解题思路

【C++】

【Java】

---

Leetcode-407. Trapping Rain Water IIhttps://leetcode.com/problems/trapping-rain-water-ii/description/

一、题目描述

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

Example 1:

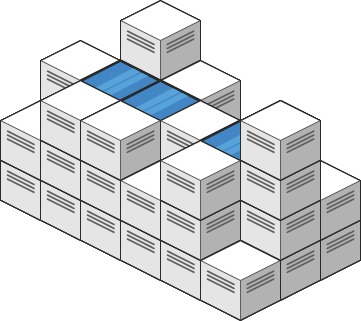
Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

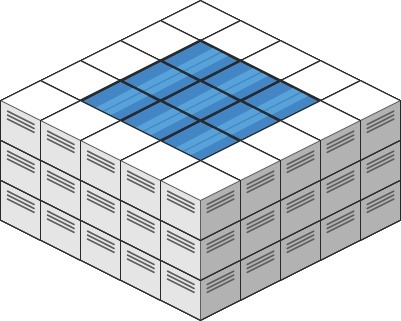
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

二、解题思路

最小堆+BFS

• 时间复杂度：O(mnlog(mn))

• 空间复杂度：O(mn)

【C++】

class Solution {
private:
    int dirs[5] = {-1, 0, 1, 0, -1};
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        if (heightMap.size() < 3 || heightMap[0].size() < 3) {
            return 0;
        }
        int m = heightMap.size(), n = heightMap[0].size(), res = 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        vector<vector<bool>> visit(m, vector<bool>(n, false));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    pq.push({heightMap[i][j], i * n + j});
                    visit[i][j] = true;
                }
            }
        }
        while (!pq.empty()) {
            pair<int, int> cur = pq.top(); pq.pop();
            for (int k = 0; k < 4; ++k) {
                int nx = cur.second / n + dirs[k], ny = cur.second % n + dirs[k + 1];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && !visit[nx][ny]) {
                    if (heightMap[nx][ny] < cur.first) {
                        res += cur.first - heightMap[nx][ny];
                    }
                    visit[nx][ny] = true;
                    pq.push({max(heightMap[nx][ny], cur.first), nx * n + ny});
                }
            }
        }
        return res;
    }
};

【Java】

class Solution {
    private int[] dirs = {-1, 0, 1, 0, -1};
    public int trapRainWater(int[][] heightMap) {
        if (heightMap == null || heightMap.length < 3 || heightMap[0].length < 3) {
            return 0;
        }
        int m = heightMap.length, n = heightMap[0].length, res = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        boolean[][] visit = new boolean[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    pq.offer(new int[]{heightMap[i][j], i * n + j});
                    visit[i][j] = true;
                }
            }
        }
        while (!pq.isEmpty()) {
            int[] cur = pq.poll();
            for (int k = 0; k < 4; ++k) {
                int nx = cur[1] / n + dirs[k], ny = cur[1] % n + dirs[k + 1];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && !visit[nx][ny]) {
                    if (heightMap[nx][ny] < cur[0]) {
                        res += cur[0] - heightMap[nx][ny];
                    }
                    visit[nx][ny] = true;
                    pq.offer(new int[]{Math.max(heightMap[nx][ny], cur[0]), nx * n + ny});
                }
            }
        }
        return res;
    }
}