决策树算法梳理

1、 信息论基础（熵 联合熵 条件熵 信息增益 基尼不纯度）

熵：熵的概念最早起源于物理学，用于度量一个热力学系统的无序程度，在信息论里面，熵是对不确定性的测量。

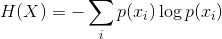
联合熵：联合熵就是度量一个联合分布的随机系统的不确定度。分布为p(x,y)的一对随机变量（X,Y），其联合熵定义为：

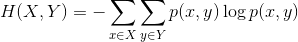
条件熵：定义事件 X 与 Y 分别取 xi 和 yj 时的条件熵为

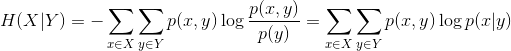
其中p(xi, yj)为 X = xi 且 Y = yj 时的概率。该条件熵应当理解为你知道Y的值前提下随机变量 X 的随机性的量。

信息增益：特征A对训练数据集D的信息增益个g(D,A)定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：

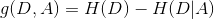
一般熵H(Y)与条件熵H(Y|X)之差称为互信息。决策树学习中的信息增益等价于类与特征的互信息。

基尼不纯度：从一个数据集中随机选取子项，度量其被错误的划分到其他组里的概率。
简单理解：一个随机事件变成它的对立事件的概率。

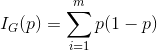
2、决策树的不同分类算法（ID3算法、C4.5、CART分类树）的原理及应用场景

决策树通常包括三个步骤: 特征选择，决策树生成和决策树剪枝
决策树的生成过程就是：使用满足划分准则的特征不断的将数据集划分为纯度更高，不确定性更小的子集的过程。
ID3：
具体方法：从根结点（root node）开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止，最后得到一个决策树。
不足：信息增益偏向取值较多的特征。

C4.5：
ID3 的后继者，并且通过动态定义将连续属性值分割成一组离散间隔的离散属性（基于数字变量），消除了特征必须被明确分类的限制。C4.5 将训练的树（即，ID3算法的输出）转换成 if-then 规则的集合。然后评估每个规则的这些准确性，以确定应用它们的顺序。如果规则的准确性没有改变，则需要决策树的树枝来解决。

CART：采用基尼系数划分数据，同时决定改特征的最优二值切分点，可针对离散和连续型，可以做分类和回归。
不足：只能进行分类。

3、回归树原理

4、决策树防止过拟合手段

当某个模型过度的学习训练数据中的细节和噪音，以至于模型在新的数据上表现很差，我们称过拟合发生了。这意味着训练数据中的噪音或者随机波动也被当做概念被模型学习了。而问题就在于这些概念不适用于新的数据，从而导致模型泛化性能的变差。可以从以下两个方面着手：
预剪枝：是在决策树的生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分即结束树的构建并将当前节点标记为叶结点。
后剪枝：是先从训练集生成一棵完整的决策树，然后自底向上地对叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化为性能提升，则将该子树替换为叶结点。泛化性能的提升可以使用交叉验证数据来检查修剪的效果，通过使用交叉验证数据，测试扩展节点是否会带来改进。如果显示会带来改进，那么我们可以继续扩展该节点。但是，如果精度降低，则不应该扩展，节点应该转换为叶节点。

5、 模型评估

分类模型误差分为：训练误差（training error）、泛化误差（generalization error）。
一个好的模型需要有较低的泛化误差和训练误差。

奥卡姆剃刀（Occam’s razor）：
给定两个具有相同泛化误差的模型，较简单的模型比较复杂的模型更可取。

悲观误差估计（pessimistic error estimate）：

是决策树的叶节点数目，e（T）为总训练误差，Nt为总训练样本数，Omega为罚项。
对二叉树来说，0.5的罚项意味着只要至少能够改善一个训练记录分类，结点就应当扩展，当1位罚项，意味着除非能够减少一个以上训练记录的误分类，否则结点不应当扩展。
先剪枝：
当达到某个条件，提前终止。例如：当观察到某个不纯度度量低于某个确定阈值时就停止扩展叶结点，但是，难点在于很难确定正确终止的阈值。

后剪枝：
初始按照最大规模生长，按照自底向上修剪决策树。修剪方式：
（1）子树替换（subtree replacement）用叶结点替代子树，叶结点的类标号为子树的多数类；
（2）子树提升（subtree raising）子树中最常使用的分支替代子树。后剪枝能产生更好的结果。
自助法（bootstrap）：
训练集是对于原数据集的有放回抽样，如果原始数据集N，可以证明，大小为N的自助样本大约包含原数据63.2%的记录。当N充分大的时候，1-（1-1/N）^(N) 概率逼近 1-e^(-1)=0.632。抽样 b 次，产生 b 个bootstrap样本，则，总准确率为（accs为包含所有样本计算的准确率）：

准确度的区间估计：
将分类问题看做二项分布，则有：
令 X 为模型正确分类，p 为准确率，X 服从均值 Np、方差 Np（1-p）的二项分布。acc=X/N为均值 p，方差 p（1-p）/N 的二项分布。acc 的置信区间：

6. sklearn参数详解，Python绘制决策树