感悟神奇的递归

一、基本使用方法

  积累了一些学习笔记，温故而知新，同时与大家分享，后面会陆续整理出来，小白学习经验，欢迎大家轻拍。

  关于递归，我们高中数学就有接触，教材中是这样定义的：当一个函数用自身来定义时就称为递归。C++允许函数是递归的，但必须要记住，C++所做的仅仅是试图遵循递归思想，不是所有的数学递归函数都能被有效的C++的递归模拟来实现。要点在于，递归函数应该像非递归函数一样只用几行就能表示出来[1]。例如：

int f(int x)
{
    if(x == 0)
        return 0;
    else
        return 2 * f(x - 1) + x * x;
}

• 1、递归是一种数学上的分而治之的思想
  a、将原问题分解为规模较小的问题进行处理。
  b、问题的分解是有限的。
  c、递归问题的一般表示法:
  f(n) ={ $$\begin{array}{*{20}{c}} {{a_n} \cup f(n - 1)}&{n > 1}\\ {{a_1}}&{n = = 1} \end{array}$$
• 2、递归在程序设计中的应用
  a、函数体中存在自我调用的函数
  b、递归函数必须有递归出口（边界条件）
  c、函数的无限递归将导致程序的崩溃

• 3、具体示例
  a、求和
  求解：Sum(n)=1+2+3…+n
  递归表示：

  Sum(n) = {

  $$\begin{array}{*{20}{c}} {n + Sum(n - 1)}&{n > 1}\\ 1&{n = = 1} \end{array}$$
  C++代码如下：

#include <iostream>
unsigned int sum(unsigned int n)
{
    if(n > 1)
    {
        return n + sum(n-1);
    }
    else
    {
        return 1;
    }
}
int main()
{
    cout << sum(100) << endl;
    return 0;
}

b、斐波那契数列
数列自身递归定义：1,1,2,3,5,8,13,21…
函数表示递归：

fac(n) ={

$$\begin{array}{*{20}{l}} {fac(n - 1) + fac(n - 2)}&{n > = 3}\\ 1&{n = = 2}\\ 1&{n = = 1} \end{array}$$
C++代码：

#include <iostream>
unsigned int fac(unsigned int n)
{
    if(n > 2)
    {
        return fac(n-1) + fac(n-2);
    }
    if((n == 2) || (n == 1))
    {
        return 1;
    }
    return 0;
}
int main()
{
    for(int i=1; i <= 10; i++)
    {
        cout << i << ":" << fac(i) << endl;
    }
    return 0;
}

c、用递归方法编写函数求字符串的长度
C++具体代码

#include <iostream>
unsigned int _strlen_(char *s)  //避免与库函数重名
{
    if(*s != '\0')
    {
        return 1 + _strlen_(s+1);
    }
    if(*s == '\0')
    {
        return 0;
    }
    return 0;
    //上述代码的另一种写法：return s ? (*s ? (1 + _strlen_(s+1)) : 0) : 0;
}
int main()
{
    cout << _strlen_("Hello优快云er!") << endl;
    return 0;
}

上述三个示例的结果如图：

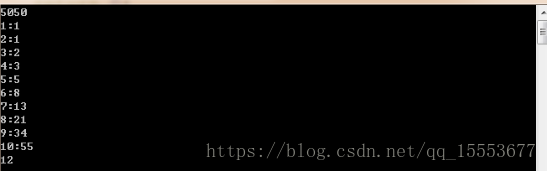
注意事项：
  解决问题的核心是如何建立递归模型，注意切勿陷入递归函数的执行细节上，学会通过程序描述问题，还要注意递归解法必须有出口，也即边界，否则无解。出口的概念我们可以这样解释：总有某些基准的情形，它们不用递归就能求解。还有一个准则需要注意，对于那些要被求解的情形，递归调用必须总能够朝着一个基准推进。

二、有趣的实例

我们来看看有趣的汉诺塔问题

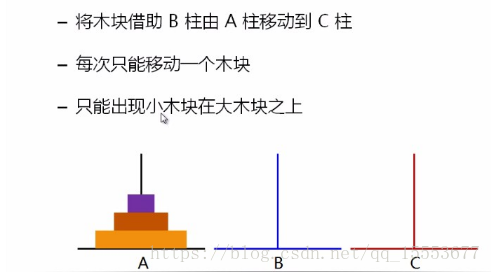
实现代码：

#include <iostream>
using namespace std;
void HanoiTower(int n, char a, char b, char c)
{
    if(n == 1)
    {
        cout << a << "-->" << c << endl;
    }
    else
    {
        HanoiTower(n-1, a, c, b);
        HanoiTower(1, a, b, c);
        HanoiTower(n-1, b, a, c);
    }
}

//测试
int main()
{
    HanoiTower(3, 'a', 'b', 'c');
    return 0;
}

方案如下图：

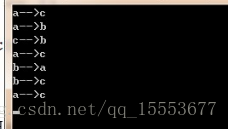
这里面的a、b、c分别代表三个柱子，箭头表示木块移动的方向。以3层塔的实验结果与手推一致，更多层塔等你去试哦！

参考文献
[1] Mark Allen Weiss，Data Structures and Algorithm Analysis in C++ Third Edition,2011.08