最小二乘法&线性回归 —> 岭回归

1.线性回归&最小二乘法

    最小二乘法的核心要义是方差达到最小值，去拟合一条曲线或者直线。而线性回归是利用最小二乘法去拟合一条直线（也可以用岭回归做线性回归）。

    （1）相关系数r（有时也用R²代表相关系数，R²即r²）

    相关系数用来做数据是否线性相关的判断

    

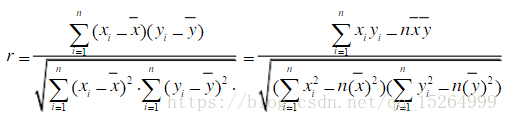
    相关系数性质：

    ①|r|<=1；

    ②|r|越大，x,y的线性相关程度越强，反之越弱；

    ③r>0，称为正相关，r<0负相关，r=0不相关。

    （2）最小二乘法

    以取得最小的方差方差为目标的拟合曲线的方法

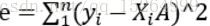    （中学用展开的方法，求出对称轴记得到抛物线的最优解）

    （3）线性回归方程

   

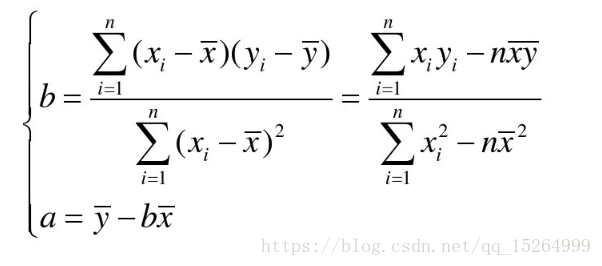
2.岭回归（又称脊回归、吉洪诺夫正则化）

    最小二乘法以数据方差的最小值为标准求得最优解，然后求得偏置a（对上方公式）。而岭回归同时考虑偏置和方差，即在方差中加入偏置（收缩方式(Shrinkage method)，又称为正则化(Regularization)），这样能同时兼顾方差和系数，对一些病态数据的拟合效果要强于最小二乘法（数据中某些发生改变，可能会严重影响数据的拟合），实际中经常用岭回归取代最小二乘法。

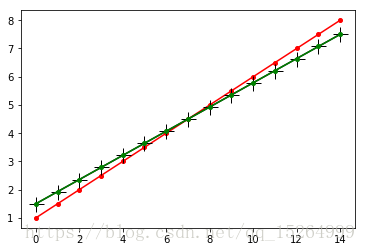
    下面是一个岭回归和最小二乘法做的拟合对比，从图中可知，区别不是很大，几乎重合：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

#构造直线函数

x = np.arange(0,15)

y = x*0.5+1
plt.figure()
plt.plot(x,y,'ro-',markersize=4)#画出原始直线

#改变图像中的某些点y值
y1 = np.copy(y)
y1[2] += 5
y1[6] -= 5

test = np.copy(x)
test = np.c_[test]

#用最小二乘法最线性回归预测
regr = linear_model.LinearRegression()
regr.fit(test,y1)
plt.plot(x, regr.predict(test),'k+-',markersize=15)

#用岭回归拟合
regr1 = linear_model.Ridge(alpha=0.1)
regr1.fit(test,y1)
plt.plot(x, regr1.predict(test),'go-',markersize=4)

    ————————————————————————————————

未完待续