[LeetCode][M0319]灯泡开关（Java）（数学）

题目描述

初始时有 n 个灯泡处于关闭状态。第一轮，你将会打开所有灯泡。接下来的第二轮，你将会每两个灯泡关闭一个。

第三轮，你每三个灯泡就切换一个灯泡的开关（即，打开变关闭，关闭变打开）。第 i 轮，你每 i个灯泡就切换一个灯泡的开关。直到第 n 轮，你只需要切换最后一个灯泡的开关。

找出并返回 n 轮后有多少个亮着的灯泡。

示例 1：

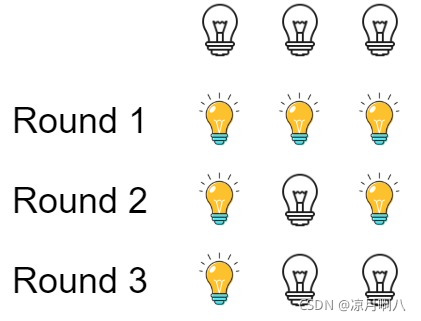
输入：n = 3
输出：1 
解释：
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭]. 

你应该返回 1，因为只有一个灯泡还亮着。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：1

提示：

0 <= n <= 109

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/bulb-switcher
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

很有意思的一道题，

首先，题目的描述要转换一下，第 i 轮，切换所有 i 的倍数的灯。
这么来看的话，到第 n 轮时，n有多少因数，就要切换多少次灯的状态。

假设n的因数是 1,2,3,4,…,n/4,n/3,n/2,n，
有没有发现，n的因数都是成对出现的！！！，
那也就意味着，灯的状态改变两次，切换回了原来的状态

注意！！！如果是这个 n 是某个数的二次方呢，那他的状态就只改变了一次。

综上所述，

• 第k个灯的状态，只能被第 1 —— k 轮修改
• 第k个灯的状态，只需要看k的二次幂是不是整数

第k轮结束时，k个灯的状态只需要看 从1——k 每个数有几个是二次方得来的数。
也就是本题解法就是 看 n 以内的正整数，有几个平方数。

反思错误

一开始想的是计算每个数，有多少个因数，结果超时了。
后来突然发现因数是成对出现的。

Java代码

class Solution {
    public int bulbSwitch(int n) {
        return (int)Math.floor(Math.sqrt(n));
    }
}

执行结果

执行耗时:0 ms,击败了100.00% 的Java用户
内存消耗:35.1 MB,击败了42.91% 的Java用户