原创文章,如需转载请保留出处
本博客为七月在线邹博老师机器学习数学课程学习笔记
本节主要内容:
-
Taylor展式
- 计算函数值
- 解释gini系数公式
- 平方根公式
-
牛顿法
- 梯度下降算法
- 拟牛顿法
- DFP
- BFGS
一.Taylor公式-Maclaurin公式
1.1 应用1:函数值计算
数值计算:初等函数值的计算(在原点展开)
计算:
求整数k和小数r,使得:
x=kln2+r,|r|≤0.5ln2
1.2 应用2:解释Gini系数
考察Gini系数、熵、分类误差率三者的关系
将f(x)=-lnx在x=1处一阶展开,忽略高阶无穷小,得到
f(x)≈1-x
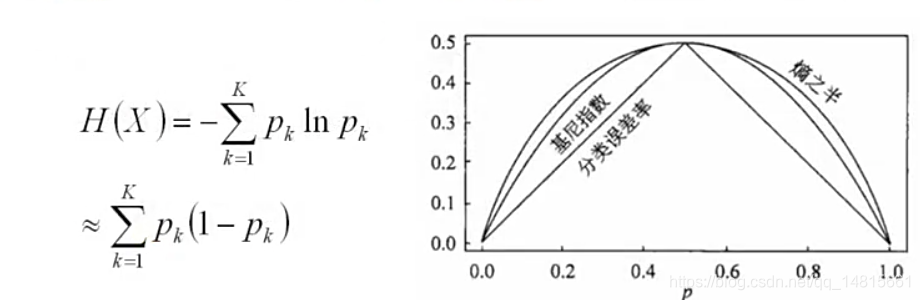
Gini系数定义:某个类别发生的概率乘以这个类别不发生的概率,把所有类别此项相加.
1.3 应用3:平方根算法
在任意点x0处Taylor展开
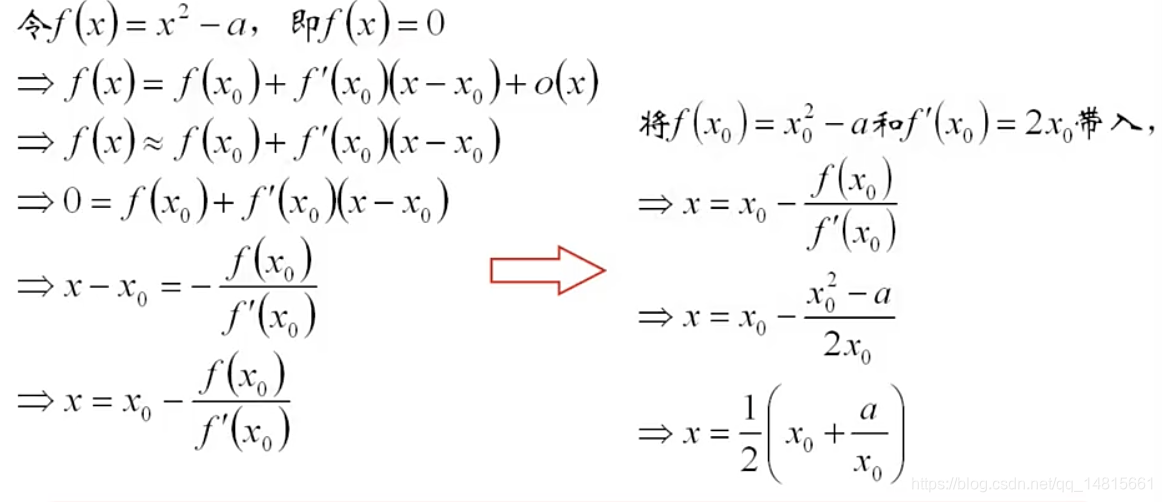
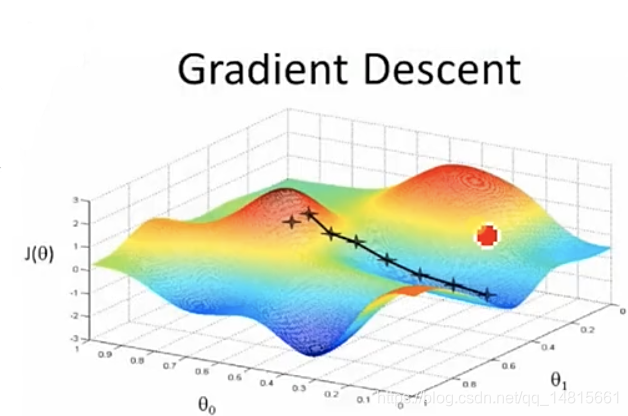
二.梯度下降算法
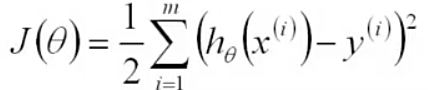
初始值θ (随机初始化)
沿着负梯度方向迭代,更新后的θ 使J(θ)更小
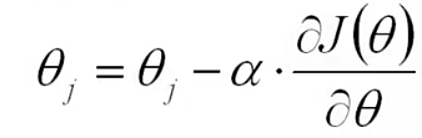
α:学习率、步长
2.1 Taylor展式
若f(x)二阶导连续,讲f(x)在Xk处Taylor展开
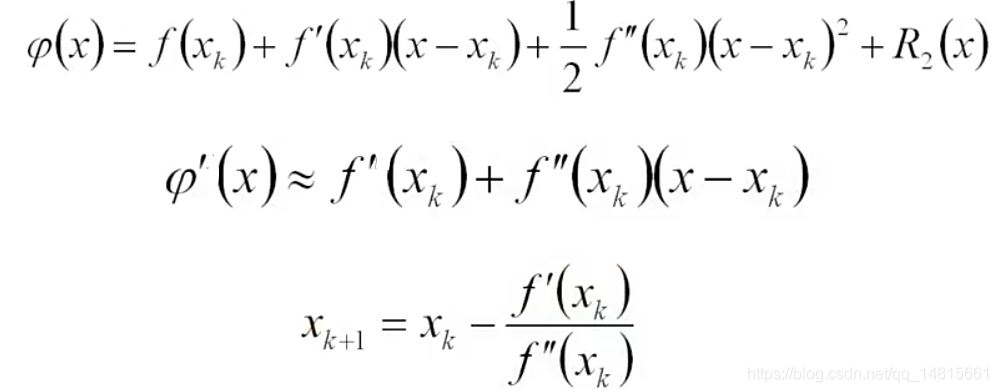
上式假设f(x)是一个一元函数,如果是一个多元函数,推导过程相同。只是f`(x)是一个向量,f``(x)是一个Hessian矩阵。
2.2 牛顿法
上述迭代公式,即是牛顿法
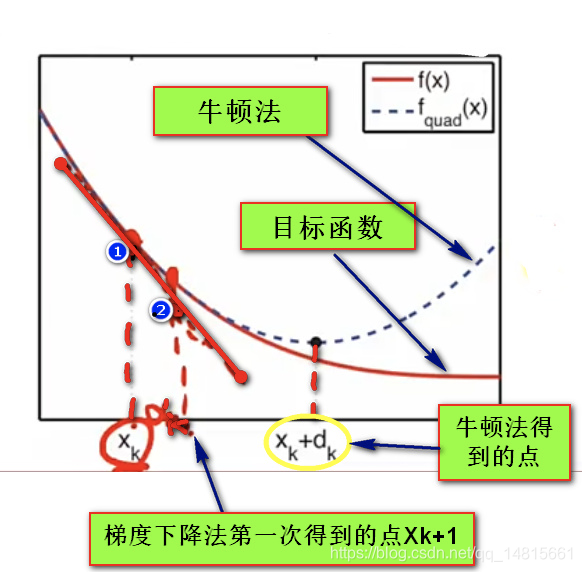
- 假设红色的曲线是目标函数
- 假设当前找到的点是Xk,我们在此处求其切线,并且沿着切线方向在横坐标移动αk的距离,这时候我们使用的算法是梯度下降算法。
- 给定Xk点的函数值,导数值,二阶导数值得到的抛物线,我们求这条抛物线的梯度为0(即最小值)的点(Xk+dk),即牛顿法是利用二次函数做的近似,而梯度下降法是利用一次函数做的近似。
2.3 牛顿法的特点
- 牛顿法具有二阶收敛性,在某些目标函数(如线性回归,Logistic回归等)问题中,它的收敛速度比梯度下降要快。
- 经典牛顿法虽然具有二次收敛性,但是要求初始点需要尽量靠近极小点,否则有可能不收敛。
- 如果Hessian矩阵奇异,牛顿方向可能根本不存在。(牛顿法公式中二阶导数为0,此时不能做分母)
- 若Hessian矩阵不是正定,则牛顿方向有可能是反方向。
- 计算过程中需要计算目标函数的二阶偏导数的逆,时间复杂度较大。
2.4Hessian矩阵非正定
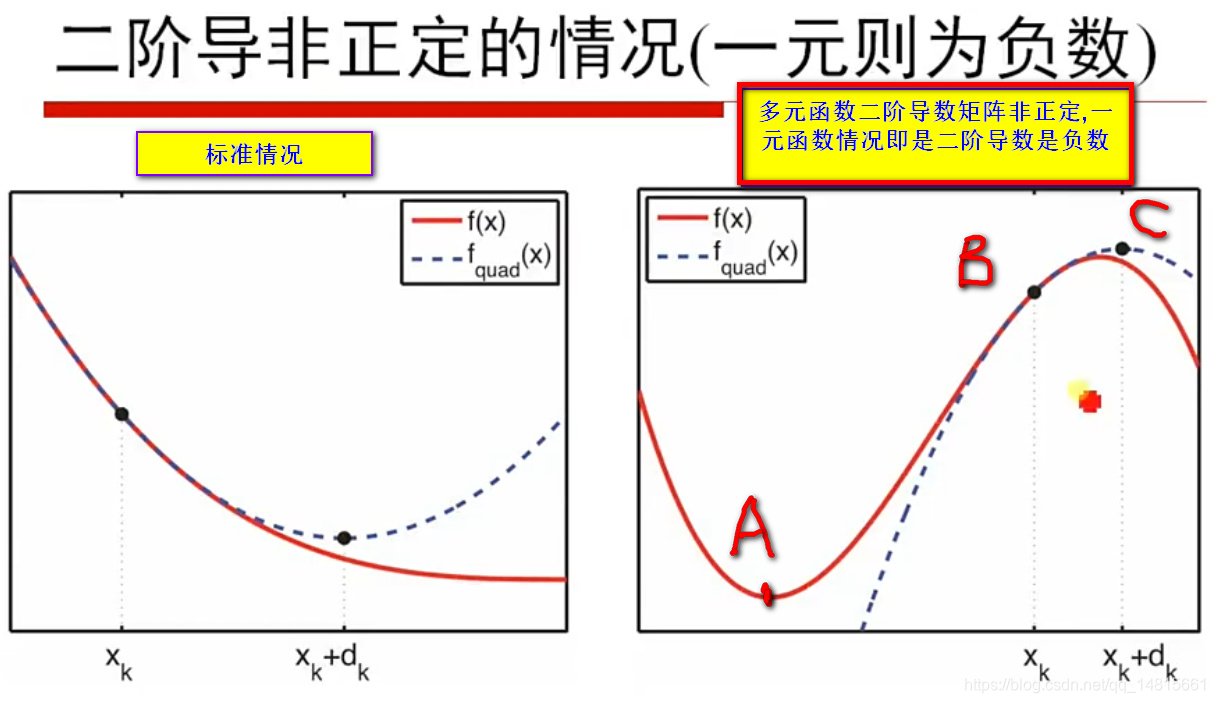
- 左边是标准情况,右边是f(x,y,z…)多元目标函数二阶导数非正定的情况,如果f(x)一元函数,则属于二阶导数为负数的情况。
- 假设红线是目标函数,最小值点在A点,假设选取的X=Xk时,此时选取的点在B点,在B点使用牛顿法得到虚线,由于得到的二次曲线是一个凹函数,二阶导数为负数,得到的极值点是虚线的最大值点。(方向错误,应向左边,取A点为最小值)。
2.5 拟牛顿法
为了解决上述问题,我们提出拟牛顿法的思路。
- 求Hessian矩阵的逆影响算法效率
- 搜索方向并非严格需要负梯度方向或者牛顿方向
- 可以用近似矩阵代替Hessian矩阵,只要满足矩阵正定,容易求导,或者可以通过若干步递推公式计算得到
- DFP: Davidon -Fletcher -Powell(三个数学家名字命名)
- BFGS: Broyden -Fletcher -Goldfarb -Shanno


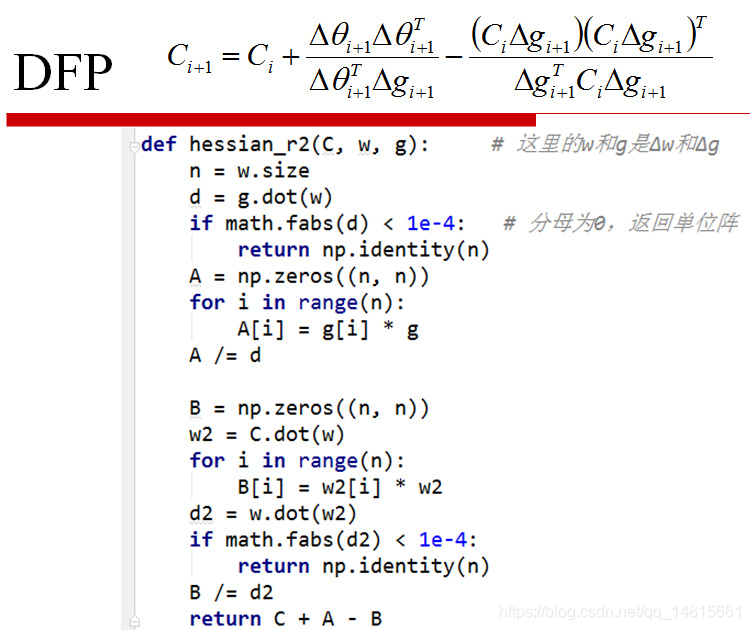

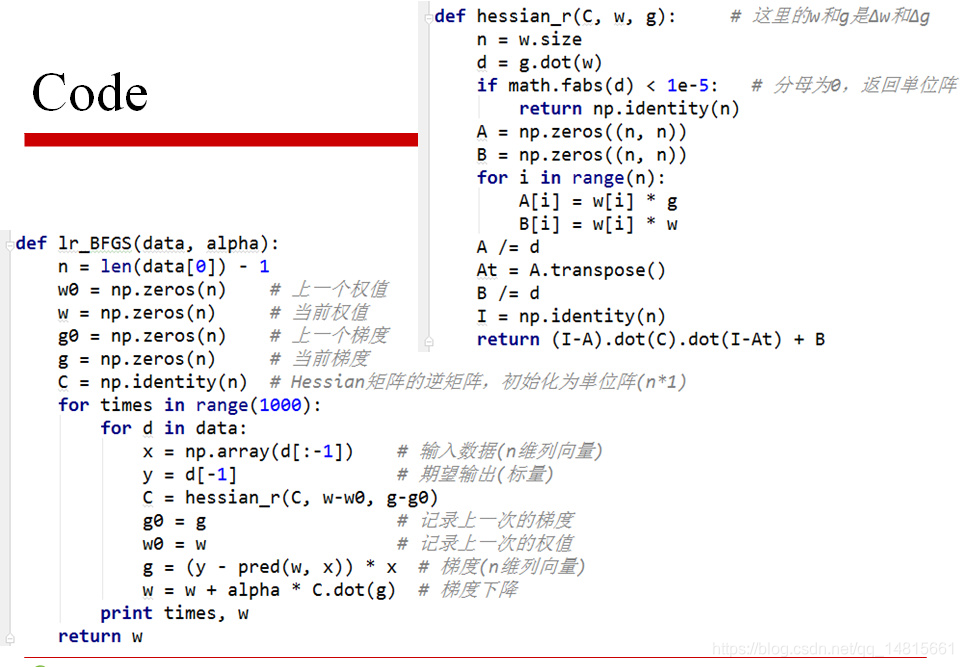







 本文深入探讨了机器学习中的数学概念,包括Taylor展式及其应用,如函数值计算、Gini系数解释和平方根算法。接着,详细介绍了梯度下降、牛顿法的原理及特点,特别强调了牛顿法在二阶收敛性和Hessian矩阵非正定时的问题。最后,讨论了解决这些问题的拟牛顿法,如DFP和BFGS算法。
本文深入探讨了机器学习中的数学概念,包括Taylor展式及其应用,如函数值计算、Gini系数解释和平方根算法。接着,详细介绍了梯度下降、牛顿法的原理及特点,特别强调了牛顿法在二阶收敛性和Hessian矩阵非正定时的问题。最后,讨论了解决这些问题的拟牛顿法,如DFP和BFGS算法。
















 175
175

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








