SRM 558 backup 1div 1

Problem Statement
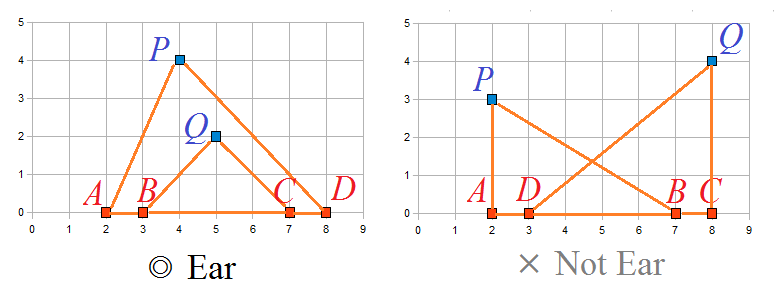
	There are some red points and blue points on the Cartesian plane. All red points are on the x-axis and all blue points are in the upper half-plane. That is, the y-coordinate of each red point is 0, and the y-coordinate of each blue point is strictly positive. Fox Ciel wants to form an ear-shaped figure using these points. She defines that the pair of four different red points A, B, C, D and two blue points P, Q is called anear if and only if all the following conditions are satisfied. Both points B and C lie strictly inside the segment AD. The angles PAD, PDA, QBC and QCB are strictly less than 90 degrees. Point Q is strictly inside of the triangle PAD. In the following image, points in the left figure form an ear while points in the right figure do not. You are given three vector <string>s redX, blueX andblueY. Concatenate all elements ofredX to get a space-separate list of integers. The i-th integer of this list represents the x-coordinate of i-th red point. In the same way,blueX andblueY encode lists of x-coordinates and y-coordinates of blue points. Your method must return the number of ways in which we can choose the four red and two blue points that form an ear.
Definition
	Class: Ear Method: getCount Parameters: vector <string>, vector <string>, vector <string> Returns: long long Method signature: long long getCount(vector <string> redX, vector <string> blueX, vector <string> blueY) (be sure your method is public)
Notes
-	The order of points in an ear does not matter. I.e., if two ears have the same four red and two blue points, they are considered the same.
Constraints
-	redX, blueX and blueY will each contain between 1 and 50 elements, inclusive.
-	Each element of redX, blueX and blueY will contain between 1 and 50 characters, inclusive.
-	After concatenating the elements of redX, the resulting string will be a single space separated list of integers.
-	After concatenating the elements of blueX, the resulting string will be a single space separated list of integers.
-	After concatenating the elements of blueY, the resulting string will be a single space separated list of integers.
-	There will be between 1 and 300 integers in each of the lists.
-	The number of integers in the lists of blueX and blueY will be the same.
-	Each integer in the lists will be between 1 and 10,000, inclusive.
-	All the integers in each list will be distinct.
-	Integers in the lists will have no leading zeros.
Examples
0)
	{"3 2 8 7"} {"5 4"} {"2 4"} Returns: 1 This case corresponds to the left figure in the statement.
1)
	{"3 2 8 7"} {"2 8"} {"3 4"} Returns: 0 This case corresponds to the right figure in the statement.
2)
	{"1 2 6 9"} {"3 6 8 5"} {"1 5 4 3"} Returns: 4 There exists only one possible combinations of A, B, C and D since there are only four red points. Possible combinations of P and Q are as follows. {(5, 3), (3, 1)} {(6, 5), (3, 1)} {(8, 4), (3, 1)} {(6, 5), (5, 3)}
3)
	{"10000"} {"10000 9999"} {"10000 9999"} Returns: 0 It is impossible to choose four red points from only one red point.
4)
	{"100 2", "00", " 39", "9", " 800 900 9", "99"} {"15", "0 250 ", "349"} {"2 3 1"} Returns: 12 Concatenate each element of the vector <string>s correctly.
5)
	{"1", " ", "2", " ", "3", " ", "4 5 6", " 7 8 9"} {"4", " ", "5", " ", "6", " 7 ", "8"} {"1", " 2 ", "3 4", " 5"} Returns: 204

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.     

有图才方便啊

要使PAD,PDA小于90度，只要X-A<X-p,X-D>X-p。QBC,QCB同理。所以要先从蓝点下手。

要使Q在P内那么PQ的连线就会交于X轴。且A、B在其左边。

typedef long long LL;

typedef long double LD;

typedef complex<LD> CMP;

class Ear { public:

longlong getCount(vector <string redX,vector <string> blueX,vector <string> blueY)

{ 

   vector<int> rx,bx,by;

{

stringstrm sin(accumulate(redX.bigin(),redX.end(),string("")));

for(int x;sin>>x;) rx.pushuback(x);

}

{

stringstrm sin(accumulate(blueX.bigin(),blueX.end(),string("")));

for(int x;sin>>x;) bx.pushuback(x);

}

{

stringstrm sin(accumulate(buleY.bigin(),blueY.end(),string("")));

for(int x;sin>>x;) by.pushuback(x);

}

int B=bx.size();

LL total =0;

for(int p=0;p<B;++p)

for(intq=0;q<B;++q)

if(by[p]>by[q])

{

int px=bx[p],py=by[p],qx=bx[q],qy,by[q];

LL a=0,b=0,c=0,d=0;

for(int i0;i<rx.size();++i)

{

int x=rx[i];

dublez=px+(qx=px)*py/double(py-qy);

if(x<min<double>(z,px))

++a;

if(min<double>(z,px)<=x&&x<px)

++b;

if(qx<x&& x<=max<double>(z,px))

++c;

if(max/,double>(z,px)<x)

++d;

}

total+=(a*(a-1)/2+a*b)*(d*(d-1)/x+d*c);

}

return total;

}

};