乘法逆元

在求解a/b%m时，可以转化为(a%(b*m))/b，转化过程如下

令k = (a/b)/m(向下取整), x = (a/b)%m;

a/b = k*m + x (x < m);

a = k*b*m + b*x;

a%(b*m) = b*x;

a%(b*m)/b = x;

得证: a/b%m = a%(b*m)/b;(公式适用于很多情况：m不必是素数，b和m也不必互质)

上面的公式适用于b较小，a需要在线求且较大的时候;

比如：求a/b的值，且另a = x^k, 求a的过程随时会爆精度所以需要对a进行取模，但是求的过程中如果是直接对a进行%mod，之后再进行a/b，会出现错误的。正确的做法是根据上述公式，在求a过程中对(b*m)取模，之后再除以一次b即可。[ a/b%m = (a%(b*m))/b%m ]

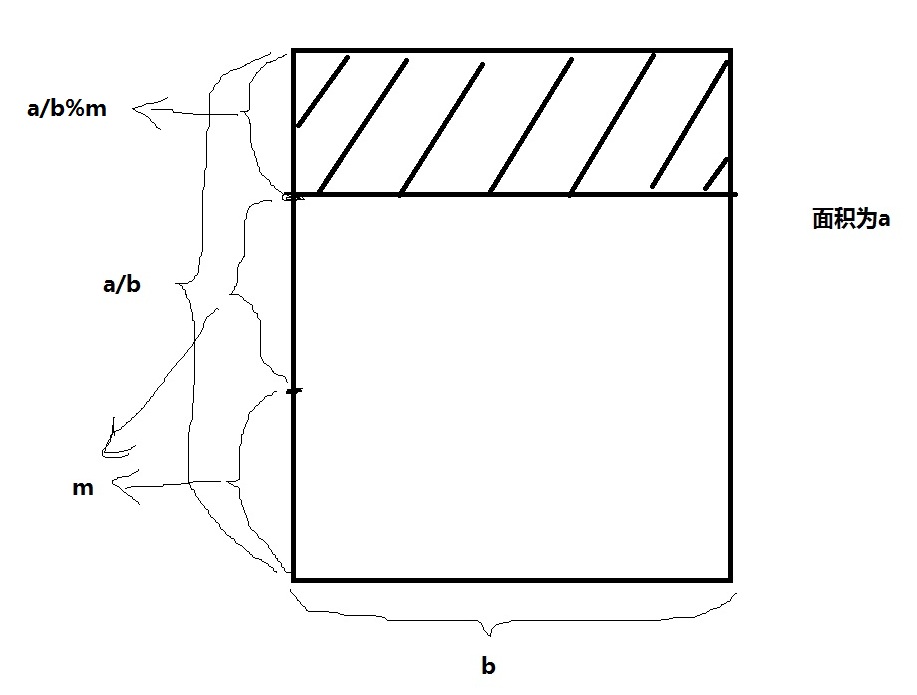
另外这个等式也可以通过如下图所示证明：

设面积为a，底边为b，则高为a/b，m为高的一部分，则a/b%m如图所示。

那a%(b*m)为阴影部分的面积，用该面积/b得到a/b%m的长。即(a%(b*m))/b = a/b%m

所有的除法取模问题都可以用这种方法，但是当b很大的时候，则会出现爆精度问题，所以引出乘法逆元，将除法取模转换为乘法取模。

逆元：

如果 b * b' % c == 1

则称b'为b模c的乘法逆元。

如果b、b'满足以上，则有：

(a/b)%c == (a*b')%c

（a/b整除，证明见附录）

举例：

2*4%7==1

则4为2模7的乘法逆元（也可以说2为4模7的乘法逆元）

则可以计算如下：

取a=20；

(a/b)%c == 20/2%7 == 10%7 == 3 

(a*b')%c == 20*4%7 == 80%7 == 3

那这里就是乘法逆元比较大的用处之一。可以将相除取模的运算转换成乘法取模的运算。

比如计算机中因为除法会导致精度的丢失，则可以用乘法逆元将相应的除法取模操作转换成乘法取模操作。

附录

用反证法证明（证明出自https://blog.youkuaiyun.com/qq_34271269/article/details/51675149）：

若b*b1 % c == 1，则( a/b ) % c ！= ( a*b1 ) % c
若我们证明这一命题是错误的，我们目的就达到了。

令，a/b   == k1*c+y1
       a*b1 == k2*c+y2
原来的证明则变成了：若b*b1 % c == 1，则 y1!=y2


两式相减，有 a/b-a*b1 == (k1-k2)*c + (y1-y2)
设 k == k1-k2
     y == y1-y2
有，a/b-a*b1 == k*c + y
左右乘以b，有 a*(1-b*b1) == k*b*c + b*y
左右模上c，
左边 == a*(1-b*b1)%c
        == ( a*( 1%c - b*b1%c ) )%c
        == 0
右边 == (k*b*c + b*y)%c
        == b*y%c

因为a/b为整除，b显然不会是0，那么y必须是0，这与命题矛盾，证毕

相关参考资料：

https://www.cnblogs.com/Tuesdayzz/p/5758670.html

https://blog.youkuaiyun.com/yo_bc/article/details/71565988

https://blog.youkuaiyun.com/triple_wdf/article/details/50994421