vector< int > preorderTraversal ( TreeNode* root) {
vector< int > res;
if ( ! root)
return res;
stack< TreeNode* > st;
st. push ( root) ;
while ( ! st. empty ( ) ) {
TreeNode* cur = st. top ( ) ;
res. push_back ( cur- > val) ;
st. pop ( ) ;
if ( cur- > right)
st. push ( cur- > right) ;
if ( cur- > left)
st. push ( cur- > left) ;
}
return res;
vector< int > preorderTraversal ( TreeNode* root) {
vector< int > res;
preorderTraversal ( root, res) ;
return res;
}
void preorderTraversal ( TreeNode* root, vector< int > & res) {
if ( root) {
res. push_back ( root- > val) ;
preorderTraversal ( root- > left, res) ;
preorderTraversal ( root- > right, res) ;
}
vector< int > inorderTraversal ( TreeNode* root) {
vector< int > res;
stack< TreeNode* > st;
TreeNode* cur = root;
while ( cur || ! st. empty ( ) ) {
while ( cur) {
st. push ( cur) ;
cur = cur- > left;
}
cur = st. top ( ) ;
st. pop ( ) ;
res. push_back ( cur- > val) ;
cur = cur- > right;
}
return res;
}
vector< int > inorderTraversal ( TreeNode* root) {
vector< int > res;
inorderTraversal ( root, res) ;
return res;
}
void inorderTraversal ( TreeNode* root, vector< int > & res) {
if ( root) {
inorderTraversal ( root- > left, res) ;
res. push_back ( root- > val) ;
inorderTraversal ( root- > right, res) ;
}
vector< int > postorderTraversal ( TreeNode * root) {
vector< int > res;
if ( ! root)
return res;
stack< TreeNode* > st1, st2;
st1. push ( root) ;
while ( ! st1. empty ( ) ) {
TreeNode* cur= st1. top ( ) ;
st1. pop ( ) ;
st2. push ( cur) ;
if ( cur- > left)
st1. push ( cur- > left) ;
if ( cur- > right)
st1. push ( cur- > right) ;
}
while ( ! st2. empty ( ) ) {
TreeNode* node= st2. top ( ) ;
st2. pop ( ) ;
res. push_back ( node- > val) ;
}
return res;
}
vector< int > postorderTraversal ( TreeNode* root) {
vector< int > res;
postorderTraversal ( root, res) ;
return res;
}
void postorderTraversal ( TreeNode* root, vector< int > & res) {
if ( root) {
postorderTraversal ( root- > left, res) ;
postorderTraversal ( root- > right, res) ;
res. push_back ( root- > val) ;
}
bool isSameTree ( TreeNode* p, TreeNode* q) {
if ( p == NULL && q == NULL )
return true ;
if ( p == NULL || q == NULL )
return false ;
return ( p- > val == q- > val)
&& isSameTree ( p- > left, q- > left)
&& isSameTree ( p- > right, q- > right) ;
} bool isMirror ( struct TreeNode* p, struct TreeNode* q) {
if ( p == NULL && q == NULL )
return true ;
if ( p == NULL || q == NULL )
return false ;
return p- > val == q- > val
&& isMirror ( p- > left, q- > right)
&& isMirror ( p- > right, q- > left) ;
}
bool isSymmetric ( TreeNode* root) {
if ( root == NULL )
return true ;
return isMirror ( root- > left, root- > right) ;
} bool isSameTree ( struct TreeNode* p, struct TreeNode* q) {
if ( p == NULL && q == NULL )
return true ;
if ( p == NULL || q == NULL )
return false ;
return p- > val == q- > val
&& isSameTree ( p- > left, q- > left)
&& isSameTree ( p- > right, q- > right) ;
}
bool preorderTraversal ( struct TreeNode * root, struct TreeNode * t) {
if ( root == NULL )
return false ;
if ( root- > val == t- > val && isSameTree ( root, t) )
return true ;
bool left = preorderTraversal ( root- > left, t) ;
if ( left == true )
return true ;
bool right = preorderTraversal ( root- > right, t) ;
return right;
}
bool isSubtree ( struct TreeNode* s, struct TreeNode* t) {
if ( t == NULL )
return true ;
return preorderTraversal ( s, t) ;
} int maxDepth ( TreeNode* root) {
if ( ! root)
return 0 ;
int left = maxDepth ( root- > left) ;
int right = maxDepth ( root- > right) ;
return ( left > right ? left : right) + 1 ;
} bool isBalanced ( TreeNode* root) {
return ( isba ( root) < 0 ? false : true ) ;
}
int isba ( struct TreeNode* root) {
if ( root == NULL )
return 0 ;
int left = isba ( root- > left) ;
if ( left < 0 )
return - 1 ;
int right = isba ( root- > right) ;
if ( right < 0 )
return - 1 ;
int tmp = left - right;
if ( ( tmp >= - 1 ) && ( tmp <= 1 ) )
return ( left > right ? left : right) + 1 ;
return - 1 ;
} int main ( ) {
string pre;
while ( cin >> pre) {
stack< char > s;
for ( auto it: pre) {
if ( it != '#' )
s. push ( it) ;
else {
if ( ! s. empty ( ) ) {
cout << s. top ( ) << " " ;
s. pop ( ) ;
}
}
}
cout << '\n' ;
}
} string tree2str ( TreeNode* t) {
if ( ! t)
return "" ;
string res = to_string ( t- > val) ;
if ( t- > left || t- > right)
res + = "(" + tree2str ( t- > left) + ")" ;
if ( t- > right)
res + = "(" + tree2str ( t- > right) + ")" ;
return res;
}
vector< vector< int >> levelOrder ( TreeNode* root) {
vector< vector< int >> res;
pre ( root, 0 , res) ;
return res;
}
void pre ( TreeNode * root, int depth, vector< vector< int >> & res)
{
if ( ! root)
return ;
if ( depth>= res. size ( ) )
res. push_back ( vector< int > { } ) ;
res[ depth] . push_back ( root- > val) ;
pre ( root- > left, depth+ 1 , res) ;
pre ( root- > right, depth+ 1 , res) ;
}
vector< vector< int >> levelOrder ( TreeNode* root) {
vector< vector< int > > res;
if ( ! root)
return res;
queue< TreeNode* > q;
TreeNode* p;
q. push ( root) ;
while ( ! q. empty ( ) ) {
vector< int > a;
int width = q. size ( ) ;
while ( width-- ) {
p = q. front ( ) ;
a. push_back ( p- > val) ;
q. pop ( ) ;
if ( p- > left)
q. push ( p- > left) ;
if ( p- > right)
q. push ( p- > right) ;
}
res. push_back ( a) ;
}
return res;
}
TreeNode* lowestCommonAncestor ( TreeNode* root, TreeNode* p, TreeNode* q) {
if ( root == nullptr || root == p || root == q)
return root;
TreeNode* left = lowestCommonAncestor ( root- > left, p, q) ;
TreeNode* right = lowestCommonAncestor ( root- > right, p, q) ;
return left == nullptr ? right : ( right == nullptr ? left : root) ;
}
TreeNode* Convert ( TreeNode* pRootOfTree)
{
if ( pRootOfTree == nullptr )
return nullptr ;
TreeNode* list_last = nullptr ;
ConvertNode ( pRootOfTree, list_last) ;
while ( list_last- > left != nullptr )
list_last = list_last- > left;
return list_last;
}
void ConvertNode ( TreeNode* cur, TreeNode * & list_last)
{
if ( cur == nullptr )
return ;
if ( cur- > left != nullptr )
ConvertNode ( cur- > left, list_last) ;
cur- > left = list_last;
if ( list_last != nullptr )
list_last- > right = cur;
list_last = cur;
if ( cur- > right != nullptr )
ConvertNode ( cur- > right, list_last) ;
}
TreeNode * preordered ( vector< int > & preorder, vector< int > & inorder, int begin, int end, int & pos) {
if ( begin>= end || pos>= preorder. size ( ) ) return NULL ;
TreeNode * r= new TreeNode ( preorder[ pos++ ] ) ;
int cur= 0 ;
for ( cur= begin; cur< end && inorder[ cur] != r- > val; ++ cur) ;
r- > left= preordered ( preorder, inorder, begin, cur, pos) ;
r- > right= preordered ( preorder, inorder, cur+ 1 , end, pos) ;
return r;
}
public :
TreeNode* buildTree ( vector< int > & preorder, vector< int > & inorder) {
int pos= 0 ;
return preordered ( preorder, inorder, 0 , inorder. size ( ) , pos) ;
}
class Solution {
public :
TreeNode* buildTree ( vector< int > & inorder, vector< int > & postorder) {
int size = inorder. size ( ) ;
TreeNode* result = buildTree1 ( inorder, postorder, size - 1 , 0 , size - 1 ) ;
return result;
}
TreeNode* buildTree1 ( vector< int > & inorder, vector< int > & postorder, int a, int a1, int b1) {
if ( a < 0 || b1 < a1 || a1 >= inorder. size ( ) || b1 < 0 )
return NULL ;
TreeNode* result = new TreeNode ( postorder[ a] ) ;
int i = 0 ;
for ( i = b1; i >= a1; i-- )
{
if ( inorder[ i] == postorder[ a] )
break ;
}
result- > right = buildTree1 ( inorder, postorder, a - 1 , i + 1 , b1) ;
result- > left = buildTree1 ( inorder, postorder, a - b1 + i - 1 , a1, i - 1 ) ;
return result;
}
} ;
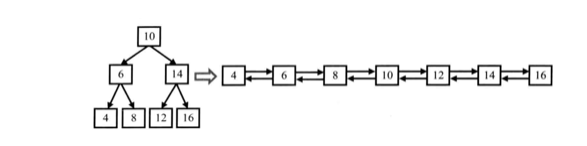
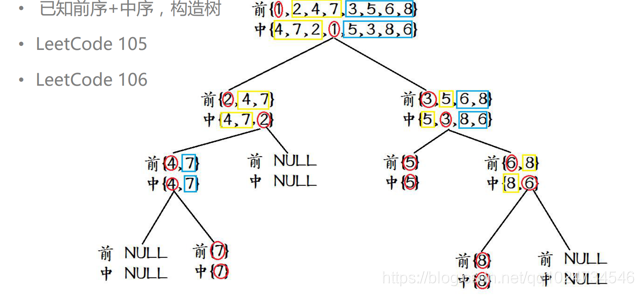










 本文详细介绍了二叉树的前序、中序、后序遍历算法,包括迭代和递归实现,并探讨了如何构建二叉树,判断树的性质如平衡性和对称性,以及树的深度和最近公共祖先等高级操作。
本文详细介绍了二叉树的前序、中序、后序遍历算法,包括迭代和递归实现,并探讨了如何构建二叉树,判断树的性质如平衡性和对称性,以及树的深度和最近公共祖先等高级操作。
















 1097
1097

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








