理解transform中的matrix

CSS中有个函数，改变六个数值就可以实现平移、旋转、缩放等2D变换效果。那么问题来了：

• 为什么是六个值？

• 修改哪些值可以实现不同的效果？

• 为什么修改这些值可以实现这样的效果？

本文探讨其背后原理，先在二维坐标系下推导公式，最后用齐次坐标统一形式。

二维平移

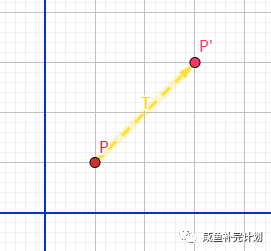
假设将点 移动 距离到点 。写出方程式：

用矩阵形式来表示二维平移方程：

二维旋转

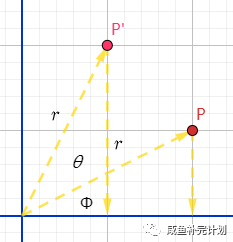
点 原始角度位置与水平线的夹角是 ， 是旋转角，点到原点的固定距离是。

在极坐标下，点的位置用点到原点的距离和水平线夹角的角度表示，点 的极坐标表示为。

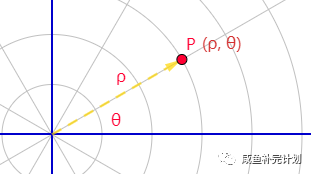
极坐标系转换为直角坐标系：

代入上述公式得到：

矩阵形式：

这个公式的旋转中心是原点，若是以任意点为旋转中心呢？css里的默认变换中心是对象中心,transform-origin可以指定变换中心，我猜测是先平移到原点进行变换，再平移回原位置，如果你知道答案请告诉我。

二维缩放

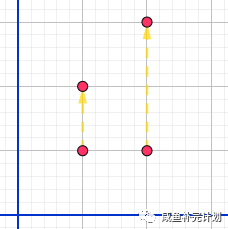
和是缩放系数，在x轴方向缩放对象，在y轴缩放对象。注意此时既缩放，又重定位。

方程：

矩阵形式：

缩放公式也是以原点为基准点进行缩放。指定固定点，只缩放不改变位置，我猜测也是先平移，缩放，再平移。

齐次坐标

将二维坐标位置表示 扩充到三维表示 ，称为齐次坐标，齐次参数 是一个非零值。此处

一般设置 ，就可以用矩阵相乘的形式来表示所有的几何变换公式。

平移

旋转

缩放

transform的matrix

到这一步就得知六个值得起源以及修改哪些值可以实现相应的效果了，使用时套用公式即可。

栗子

平移

transform: matrix(1,0,0,1,50,50);

旋转

若旋转角度为30°

transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);

缩放

若比例均为2

transform: matrix(2, 0,0,2,0,0)

如此一来，如果你想实现其他变换效果，也可以按照同样的思路，一步步推导结果。

例如

变形

MDN中已给出结果，来玩玩儿：

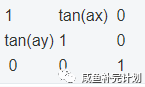
transform: matrix(1, 1, 0, 1, 0, 0)

复合变换

平移 + 缩小，将变换矩阵相乘即可

transform: matrix(0.5, 0, 0, 0.5, 25, 25)

参考资料

• 使用的绘图工具：GeoGebra
  

• 配色参考：经典三原色 + NIPPON COLORS

• LateX语法写公式

• 计算机图形学（第三版）—— Donald Hearn/M.Pauline Baker著

• 线性代数简明教程第二版——陈维新/编著