一、项目简介
在客户精细化运营时代,如何通过数据挖掘实现精准营销和利润最大化?本项目以航空公司客户数据为例,基于 K-Means聚类算法 构建客户价值评估模型,从 飞行次数、入会时间、平均折扣率、时间间隔差值、总里程、平均每公里票价 6个核心维度,将客户划分为 5类典型群体,针对不同类型客户,进行精准营销,对不同价值的客户类别提供个性化服务,制定相应的营销策略 实现利润最大化,建立客户价值评估模型。

二、项目核心流程
- 数据预处理:清洗航空公司客户数据,对6维特征进行标准化处理(消除量纲差异)。
- 聚类建模:使用肘部法则和轮廓系数确定最优聚类数(K=5),并通过K-Means算法完成客户分群。
- 客户分层命名:根据聚类结果,结合业务逻辑,将5类客户命名为 “低活跃度/低价值用户”“流失风险老客户”“高价值核心客户”“高端商务/高折扣敏感客户”“季节性/波动型客户”,并分析其特征。
- 价值对比与策略制定:量化每类客户的生命周期价值(CLV),设计差异化营销策略(如定向优惠券、会员权益升级、流失预警干预等)。
- 代码实战:提供完整的Python实现(含数据加载、聚类分析、可视化及策略建议),适合数据分析师和营销人员复现。
三、5类客户群体命名与特征
| 簇编号 | 分类名称 | 核心特征 | 关键策略 |
|---|---|---|---|
| 1 | 低活跃度/低价值用户 | 人数多,数据全面低于平均 | 激活、分层运营 |
| 2 | 流失风险老客户 | 老客户但活跃度下降 | 挽回、预警 |
| 3 | 高价值核心客户 | 高频、高里程、高票价 | 保留、VIP服务 |
| 4 | 高端商务/高折扣敏感客户 | 高票价+高折扣,舱位等级高 | 保留+发展、企业合作 |
| 5 | 季节性/波动型客户 | 飞行时间间隔差异大,季节性集中 | 精准营销、行为预测 |
四、项目价值
通过本项目,读者可以掌握:
- 如何从多维度构建客户价值评估模型;
- 如何将无监督学习(K-Means)应用于商业场景,实现客户分层;
- 如何基于聚类结果制定可落地的精准营销策略,提升客户留存与利润;
- 如何通过可视化分析(如雷达图、热力图)直观展示客户群体差异。
适合人群:数据分析师、市场营销人员、机器学习初学者。
代码语言:Python(Pandas、Scikit-learn、Matplotlib/Seaborn)。
五、项目代码
项目使用数据集:air_data.csv 该数据集给出了关于 62988 个客户的基本信息和在观测窗口内的消费积分等相关信息,其中包含了会员卡号、入会时间、性别、年龄、 会员卡级别、在观测窗口内的飞行公里数、飞行时间等 44 个特征属性。
1、导入数据
1.1、导入数据包
1.1.1 Pandas库:读取 CSV 文件、处理缺失值、筛选数据等。
1.1.2 NumPy 库:用于数值计算、矩阵运算、生成随机数据等。
1.1.3 KMeans 聚类算法:从 scikit-learn 库中导入。KMeans 是一种无监督学习算法,用于将数据分成 K 个簇(分组),基于样本间的距离(如欧氏距离)进行分类。常用于客户分群、图像压缩、异常检测等。👇点击了解KMeans算法原理
1.1.4 pyplot :用于绘制折线图、散点图、直方图等。
import pandas as pd #一定要注意pandas的大小写问题
import numpy as np #numpy 一样也要注意大小写问题
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt1.2、数据分析
1.2.1、指定文件路径:如果文件不在当前工作目录,需写完整路径(如 "C:/data/air_data.csv")
1.2.2、读取csv文件
1.2.3、打印数据形状:快速了解数据规模。
1.2.4、打印数据信息: 检查数据质量(如是否有缺失值)、列的数据类型是否正确
1.2.5、打印前5行数据:快速预览数据内容,确认读取是否正确
datafile='air_data.csv' #指定文件路径:如果文件不在当前工作目录,需写完整路径(如 "C:/data/air_data.csv")
data=pd.read_csv(datafile,encoding='utf-8') #读取csv文件,赋值给变量 data
print(data.shape) #打印数据形状,快速了解数据规模
#print(data.info()) #打印数据信息:检查数据质量
#print(data[0:5]) #打印前五行,快速预览,确实读取是否正确1.3、数据特征工程
1.3.1 清洗异常、缺失值:清除票价为0,但是飞行公里数不为了0的不合理数据。因占比小这里直接删除
data = data[(data["SUM_YR_1"] != 0) | (data["SUM_YR_2"] != 0)] #删除票价为0的数据;|(逻辑或)合并两个条件,表示 只要 SUM_YR_1 或 SUM_YR_2 其中一个不为 0,就保留该行
#print(data.shape)
data = data[data["SUM_YR_1"].notnull() & data["SUM_YR_2"].notnull()] #删除票价是空的数据;&:逻辑与要求两列同时非空
#print(data.shape)1.3.2数据初始特征提取
①提取主要特征:仅保留与客户价值分析相关的核心字段。使用:FFP_DATE(入会时间)、LOAD_TIME(观测窗口的结束时间)、FLIGHT_COUNT(飞行次数)、SUM_YR_1(第一年总票价)、SUM_YR_2(第二年总票价)
SEG_KM_SUM(观测窗口总飞行公里数)、AVG_INTERVAL(平均乘机时间间隔)、MAX_INTERVAL(观察窗口内最大乘机间隔)、avg_discount(平均折扣率)
②进行数据降为:减少计算量,避免无关列干扰模型。
③标准化输入:为后续步骤(如计算RFM得分、客户分群)准备结构化的特征表。
filter_data = data[[ "FFP_DATE", "LOAD_TIME", "FLIGHT_COUNT", "SUM_YR_1", "SUM_YR_2", "SEG_KM_SUM", "AVG_INTERVAL", "MAX_INTERVAL", "avg_discount"]]
#print(filter_data[0:5])数据清洗后剩余62044条,清除的异常样本比例不足15%,不会对分析结果产生较大影响。
1.3.3日期格式转换
在观察数据时,可知观测窗口的结束时间(LOAD_TIME)、入会时间(FFP_DATE)为字符串,所以我们需要将这两个特征转换为 Pandas 的 datetime 格式。
datetime格式支持高效的时间计算,包括:
①可直接应用于时间差计算,即时间相减
②时间单位提取,通过.dt 访问器快速提取年、月、日、星期等。
③按时间排序
④生成时间序列图表
data["LOAD_TIME"]=pd.to_datetime(data["LOAD_TIME"])#pd.to_datetime() 是 Pandas 提供的函数,用于将输入数据解析为 datetime64[ns] 类型(即标准的时间戳格式)
data['FFP_DATE']=pd.to_datetime(data['FFP_DATE'])1. 3.4特征转换
①计算入会时间:观测窗口的结束时间-入会时间
data['入会时间']=data['LOAD_TIME']-data['FFP_DATE']②计算平均每公里票价:将两年票价总和(SUM_YR_1 + SUM_YR_2)除以飞行总里程(SEG_KM_SUM),得到单位里程票价
data['平均每公里票价']=(data["SUM_YR_1"]+data["SUM_YR_2"])/data['SEG_KM_SUM']③计算时间间隔差值:最大时间间隔与平均时间间隔的差值,衡量飞行频率的稳定性
data['时间间隔差值']=data['MAX_INTERVAL']-data['AVG_INTERVAL']④重命名列:提高可读性,将英文列名改为中文,更易理解
deal_data=data.rename( #data.rename()是Pandas DataFrame 的方法,用于修改列名(columns)或索引名(index)。
columns={ #columns={原列名: 新列名, ...},传入一个字典,键是原始列名,值是新的列名
"FLIGHT_COUNT": "飞行次数",
"SEG_KM_SUM": "总里程",
"avg_discount": "平均折扣率"
},
inplace=False #表示不直接修改原始 DataFrame data,而是返回一个新的 DataFrame(赋值给 deal_data)。True,则会直接修改 data,且不会返回新对象(此时 deal_data 会是 None)
)⑤重新筛选特征:从重命名后的数据 deal_data 中筛选出需要的6个特征,保存到 filter_data
filter_data = deal_data[[
"入会时间", "飞行次数", "平均每公里票价", "总里程", "时间间隔差值", "平均折扣率"
]]
#print(filter_data[0:5])
⑥转换入会时间为数值(天数):将 入会时间(timedelta 类型)转换为整数(纳秒单位),再除以 (60*60*24*10**9) 转换为天数。
60*60*24*10**9 是将纳秒转换为天的系数(1天=86400秒=86400×10⁹纳秒)。
filter_data['入会时间'] = filter_data['入会时间'].astype(np.int64) / (60*60*24*10**9)
#print(filter_data[0:5])
⑦检查数据类型:输出 filter_data 的列名、非空值数量和数据类型,确认数据预处理是否正确
print(filter_data.info())
1.3.5数据标准化
对数据进行标准化,将数据按列(特征)转换为均值为 0、标准差为 1 的分布。标准化后,所有特征在相同尺度上,避免某些特征因数值范围大而主导聚类
filter_zscore_data = (filter_data - filter_data.mean(axis=0)) / (filter_data.std(axis=0)) #filter_data.mean(axis=0):计算每列的均值,filter_data.std(axis=0):计算每列的标准差,(filter_data - 均值) / 标准差:对每个值进行标准化
#filter_zscore_data[0:5] # 查看前5行标准化后的数据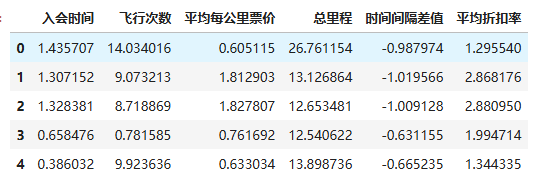
1.3.6K-Means 聚类模型初始化
kmodel = KMeans(n_clusters=4, n_init='auto') #n_clusters=4:将数据分成 4 个簇;n_init='auto'(自动选择最佳初始中心次数)1.3.7寻找K值和肘点
对于 K-Means 方法,k 的取值是一个难点,因为是无监督的聚类分析问题,所以不存在绝对正确的值,我们要测试不同簇数量(k值)下K-Means聚类算法的SSE(Sum of Squared Errors,误差平方和)变化,用于帮助确定最佳的k值(肘部法则)。
①定义个计算距离的小工具(distEclud函数)
计算两个向量之间的欧式距离的平方(用于比较远近),在K-Means聚类中判断数据点属于哪个组。我们这里没有选择开平方,因为在机器学习中(比如K-Means聚类),我们通常只需要比较距离的相对大小,而不需要具体的距离值,用开平方不会改变大小关系,但是计算更消耗。
def distEclud(vecA,vecB):
vecA = np.array(vecA)
vecB = np.array(vecB)
diff =vecA-vecB #计算两个向量的差, 比如 vecA=[1,2], vecB=[4,6] → [1-4, 2-6] = [-3, -4]
squared_diff=np.power(diff,2) #对差值逐个平方。np.power(base, exponent),base底数,exponent指数,可以是单位数字、列表或 NumPy 数组
sum_squared=np.sum(squared_diff) #把所有平方值相加
return sum_squared #返回结果(欧氏距离的平方)
#distEclud([1,2], [4,6]) ② K-Means 聚类算法的肘部法则(Elbow Method)分析,用于确定最佳的聚类数(k 值)
def test_Kmeans_nclusters(data_train): #定义一个函数,输入训练数据data_train,通过肘部法则选择最优k值
data_train = data_train.values if hasattr(data_train, 'values') else data_train #检查 data_train 是否有 .values 属性,用于区分 Pandas DataFrame 和 NumPy 数组。避免后续计算因数据格式不兼容报错
nums = range(2, 10) #定义要测试的聚类数 k 的范围(从 2 到 9)
SSE = [] #空列表,用于存储每个 k 值对应的 SSE 值
for num in nums: #遍历不同的k值
kmodel = KMeans(n_clusters=num, n_init='auto') #创建创建 K-Means 模型:n_clusters=num:设置当前聚类数;n_init='auto':自动选择最优的初始化次数(避免局部最优)
kmodel.fit(data_train) #拟合数据:kmodel.fit(data_train),计算聚类中心和样本标签
# 向量化计算 SSE
distances = np.sum((data_train - kmodel.cluster_centers_[kmodel.labels_]) ** 2, axis=1)
sse = np.sum(distances)
print("簇数是", num, "时; SSE 是", sse)
SSE.append(sse)
return nums, SSE
③绘制图表,选出合适的k值
#主程序入口, 执行肘部法则分析,结果可用于选择最佳 k 值
if __name__ == '__main__':
nums, SSE = test_Kmeans_nclusters(filter_zscore_data)
# 绘制肘部法则图
plt.figure(figsize=(8, 5))
plt.plot(nums, SSE, 'bo-', markersize=8, linewidth=2)
plt.xlabel('Number of Clusters (k)', fontsize=12)
plt.ylabel('Sum of Squared Errors (SSE)', fontsize=12)
plt.title('Elbow Method for Optimal k', fontsize=14)
plt.xticks(nums) # 确保 x 轴显示整数 k 值
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()运行结果
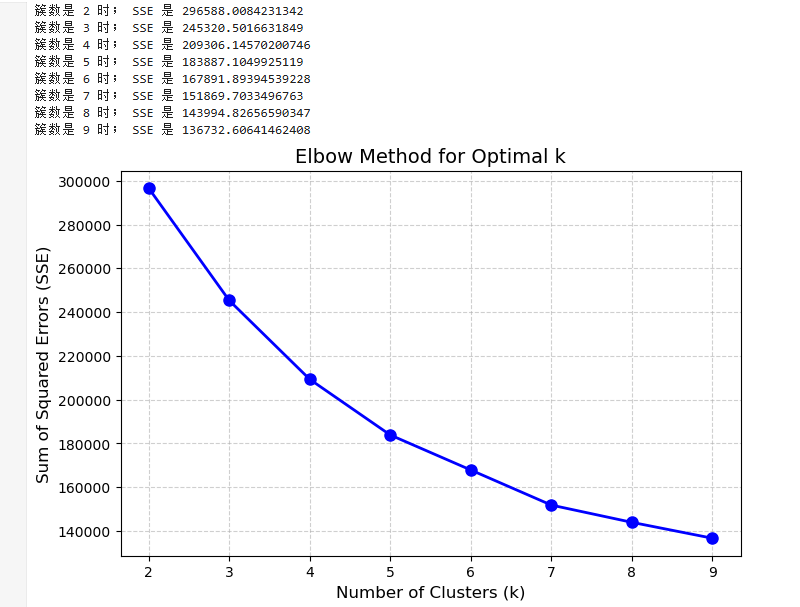
2、k值验证
肘部法的目标是找到一个 SSE(误差平方和)下降速度明显变缓的点,即“肘部”。SSE 衡量样本到其所属簇中心的距离平方和,随着 k 增大,SSE 会逐渐减小。但当 k 超过某个值后,SSE 的下降幅度会显著变缓,此时增加簇数带来的收益递减。
经上方图表分析:
k=2 到 k=4:SSE 从 300,000 快速下降到约 210,000,下降幅度较大。
k=4 到 k=5:SSE 从 210,000 下降到约 180,000,下降幅度仍然明显,但开始变缓。
k=5 之后:SSE 继续下降,但下降速度明显减慢(如 k=5 到 k=6 仅下降约 15,000)。
由此看出:
k=4:是 SSE 下降速度开始变缓的转折点(即“肘部”),此时增加簇数带来的 SSE 改善开始减弱。
k=5:如果希望更精细的聚类,可以选择 k=5,因为此时 SSE 仍有较明显的下降,但需权衡模型复杂度
所以我们将分别尝试k=4与k=5
当k=4时
# 1. 创建 K-Means 模型(注意:n_jobs 已废弃,改用 n_init='auto')
kmodel = KMeans(n_clusters=4, n_init='auto', random_state=42) # 固定随机种子保证可复现
kmodel.fit(filter_zscore_data)
# 2. 统计结果
r1 = pd.Series(kmodel.labels_).value_counts().sort_index() # 按簇编号排序
r2 = pd.DataFrame(kmodel.cluster_centers_, columns=filter_zscore_data.columns) # 添加列名
# 3. 合并簇中心和样本数量
r = pd.concat([r2, r1], axis=1)
r.columns = list(filter_zscore_data.columns) + ['类别数目'] # 重命名列
# 4. 雷达图绘制
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, polar=True)
# 特征名称(需与 filter_zscore_data 的列名一致)
features = list(filter_zscore_data.columns) # 自动获取特征名,避免硬编码
N = len(features)
# 计算全局最大值和最小值(用于设置雷达图范围)
max_val = r.iloc[:, :-1].values.max() # 排除最后一列(样本数)
min_val = r.iloc[:, :-1].values.min()
# 绘制每个簇的雷达图
for i, row in enumerate(r.values):
center = np.concatenate((row[:-1], [row[0]])) # 闭合雷达图
angles = np.linspace(0, 2*np.pi, N, endpoint=False).tolist() + [0] # 角度闭合
ax.plot(angles, center, 'o-', linewidth=2, label=f"簇 {i+1} ({int(row[-1])}人)")
ax.fill(angles, center, alpha=0.25)
# 设置雷达图属性
ax.set_thetagrids(np.degrees(angles[:-1]), features, fontsize=12)
ax.set_ylim(min_val - 0.1, max_val + 0.1)
ax.set_title('客户群特征分析图', fontsize=15, pad=20)
ax.grid(True)
plt.legend(loc='upper right', bbox_to_anchor=(1.3, 1.1))
plt.tight_layout() # 防止标签溢出
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # Windows
plt.rcParams['axes.unicode_minus'] = False
plt.show()执行结果
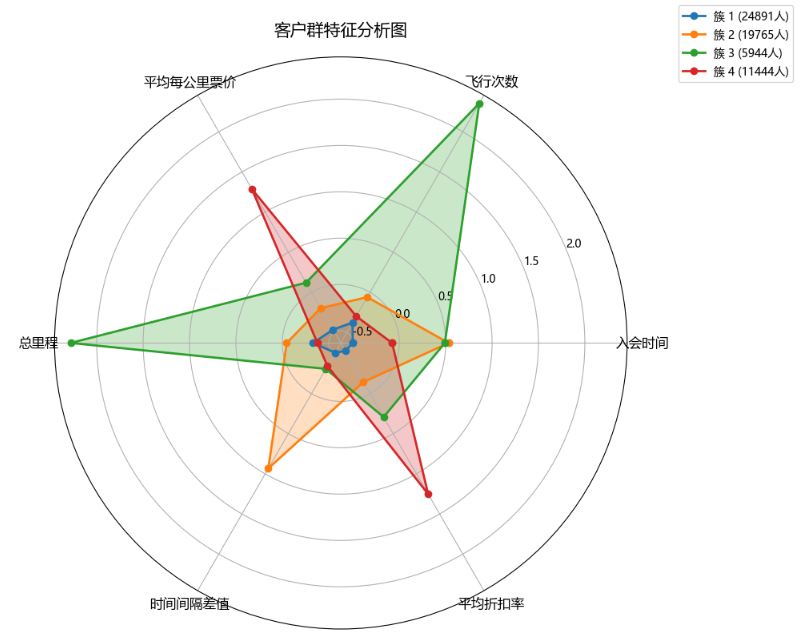
当k=5时,修改上方代码中,n_clusters=5,执行结果
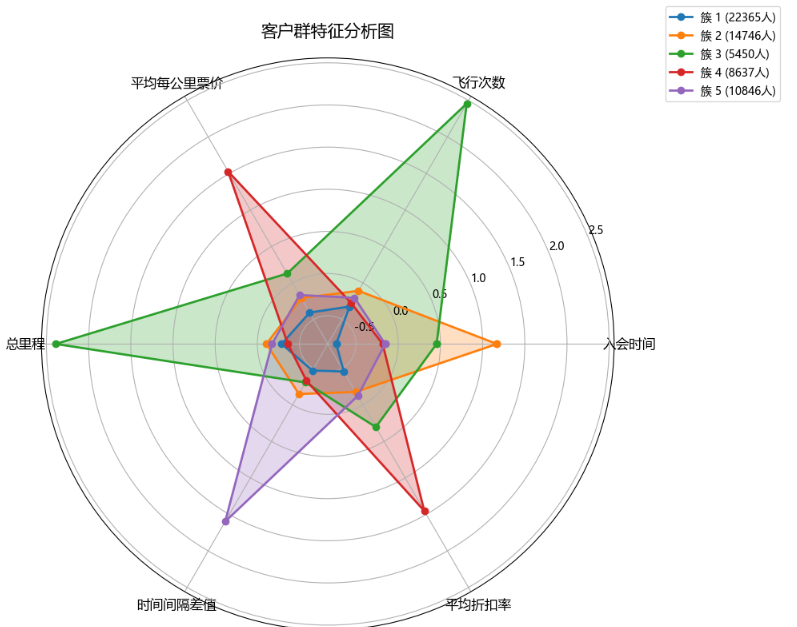
六、结果分析
当 k 取值 4 时,每个人群包含的信息比较复杂,且特征不明显
当 k 取值 5 时,分析的结果比较合理,分出的五种类型人群都有自己的特点又不相互重复
综上,当 k 取值为 5 时,得到最好的聚类效果,将所有的客户分成 5 个人群,再进一步分析可以得到以下结论:
1.低活跃度/低价值用户
第1簇人群,22365 人,各方面的数据都是比较低的,属于一般或低价值用户。可能是沉默用户或价格敏感型客户,对品牌忠诚度低
策略建议:
- 激活策略:通过定向优惠券(如满减、折扣)或积分奖励刺激首次或重复消费。
- 分层运营:若长期无互动,可降级为潜在客户,减少运营资源投入。
2.流失风险老客户
第2簇人群,14746人,最大的特点就是入会的时间较长,属于老客户按理说平均折扣率应该较高才对,但是观察窗口的平均折 扣率较低,而且总里程和总次数都不高,分析可能是流失的客户,需要在争取一下,尽量让他们“回心转意”;
策略建议:
- 挽回策略:
- 专属老客户回馈活动(如额外积分、免费升舱券)。
- 满意度调研,针对性改进服务短板。
- 预警机制:标记为高流失风险客户,定期跟踪消费行为变化。
3.高价值核心客户
第3簇人群,5450 人, 总里程和飞行次数都是最多的,而且平均每公里票价也较高,是重点保持对象。可能是高频商务旅客或高净值人群,对价格不敏感,注重服务品质。
策略建议:
- 保留策略:
- 提供VIP服务(如专属休息室、快速安检通道)。
- 定制化权益(如免费行李额、优先选座)。
- 防流失:定期回访,主动解决潜在不满。
4.高端商务/高折扣敏感客户
第4簇人群,8637 人,最大的特点就是平均每公里票价和平均折扣率都是最高的,应该是属于乘坐高等舱的商务人员,应该重 点保持的对象,也是需要重点发展的对象,另外应该积极采取相关的优惠政策是他们的乘坐次数增加。
策略建议:
- 双管齐下:
- 保留:提供弹性票价套餐(如“商务往返优惠”)、舱位升级权益。
- 发展:通过企业合作协议(如公司差旅计划)批量锁定客户。
- 数据分析:跟踪其出行规律,优化航班时刻和舱位分配。
5.季节性/波动型客户
第5簇人群,10846 人,最大的特点是时间间隔差值最大,分析可能是“季节型客户”,一年中在某个时间段需要多次乘坐飞机 进行旅行,其他的时间则出行的不多,这类客户我们需要在保持的前提下,进行一定的发展;可能是旅游群体或特定行业从业者(如教师、项目制工作者)
策略建议:
- 精准营销:
- 提前推送季节性优惠(如暑期家庭套餐、寒假学生折扣)。
- 联合旅游平台推出“机票+酒店”捆绑产品。
- 行为预测:基于历史数据预测其出行高峰,提前触达。
分析完毕,结果暗合市场的二八法则的,价值不大的第二三簇的客户数最多,而价值较大的第四五簇的人数较少。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










