13蓝桥省赛a组+16蓝桥省赛a

最新推荐文章于 2019-03-23 20:45:15 发布

原创最新推荐文章于 2019-03-23 20:45:15 发布 · 322 阅读

0 ·

CC 4.0 BY-SA版权

蓝桥专栏收录该内容

18 篇文章

订阅专栏

本文主要解析了蓝桥省赛A组的部分编程题目，包括‘振兴中华’、‘搭积木’、‘寒假作业’等。题目涵盖搜索、暴力循环、全排列等解题方法，涉及数字积木、数学问题、逆波兰表达式等多元化的算法应用。

5-1

标题: 振兴中华

小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

地上画着一些格子，每个格子里写一个字，如下所示：（也可参见p1.jpg）

从我做起振
我做起振兴
做起振兴中
起振兴中华

比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。


要求跳过的路线刚好构成“从我做起振兴中华”这句话。

请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

答案是一个整数，请通过浏览器直接提交该数字。

注意：不要提交解答过程，或其它辅助说明类的内容。

一共有(8分) 种可能的跳跃路线

思路：搜索。

代码：

#include<iostream>
using namespace std;
int mapp[4][5] = {1,2,3,4,5,
                  2,3,4,5,6,
                  3,4,5,6,7,
                  4,5,6,7,8  };
int res = 0;
void dfs(int x,int y,int step)
{
    if(step>8)
        return ;
    if(step==8&&mapp[x][y]==8)
    {
        res++;
        return;
    }
    if(x+1<4&&mapp[x+1][y]==step+1)
        dfs(x+1,y,step+1);
    if(y+1<5&&mapp[x][y+1]==step+1)
        dfs(x,y+1,step+1);
}
int main()
{
   dfs(0,0,1);
   printf("%d",res);
}

答案：35

2.某君新认识一网友。

当问及年龄时，他的网友说：

“我的年龄是个2位数，我比儿子大27岁,

如果把我的年龄的两位数字交换位置，刚好就是我儿子的年龄”

请你计算：网友的年龄一共有多少种可能情况？

提示：30岁就是其中一种可能哦.

请填写表示可能情况的种数。

注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

思路：暴力循环

代码：略

答案：7

搭积木

小明最近喜欢搭数字积木，

一共有10块积木，每个积木上有一个数字，0~9。

搭积木规则：

每个积木放到其它两个积木的上面，并且一定比下面的两个积木数字小。

最后搭成4层的金字塔形，必须用完所有的积木。

下面是两种合格的搭法：

请你计算这样的搭法一共有多少种？

请填表示总数目的数字。注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

思路：将0-9放到数组里，然后挨个判断，利用c++中的next_permutation，将0-9全排列。

注意：next_permutation最大能算的为12,13；其中算12的全排列就需要两分钟。用的时候可能会超时。

并且这个函数会忽略一开始的全排列。比如123456的全排列应该有6!个，但是利用此函数算出的全排列有6！-1个。

即忽略“123456”

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int main()
{
	int a[10] = {0,1,2,3,4,5,6,7,8,9};
	int counts = 1;//0,1,2,3,4,5,6,7,8,9符合条件 
	while(next_permutation(a+1,a+10))//0只能做a[0] 
	{
		if(a[1]<a[3]&&a[1]<a[4]&&a[2]<a[4]&&a[2]<a[5]&&a[3]<a[6]&&a[3]<a[7]&&a[4]<a[7]&&a[4]<a[8]&&a[5]<a[8]&&a[5]<a[9])
			counts++;
	}
	printf("%d",counts);
}

答案：768

寒假作业

现在小学的数学题目也不是那么好玩的。

看看这个寒假作业：

   □ + □ = □
   □ - □ = □
   □ × □ = □
   □ ÷ □ = □

(如果显示不出来，可以参见【图1.jpg】)

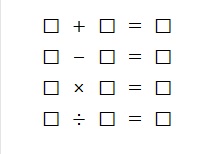
每个方块代表1~13中的某一个数字，但不能重复。

比如：

 6  + 7 = 13
 9  - 8 = 1
 3  * 4 = 12
 10 / 2 = 5

以及：

 7  + 6 = 13
 9  - 8 = 1
 3  * 4 = 12
 10 / 2 = 5

就算两种解法。（加法，乘法交换律后算不同的方案）

你一共找到了多少种方案？

请填写表示方案数目的整数。

注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

思路：搜索

#include <stdio.h>
int num[4][3];
int vis[14],sum;
void dfs(int step)
{
    int x=step/3;
    int y=step%3;
    if(step==12)
	{
        if(num[3][1]!=0&&num[3][0]%num[3][1]==0&&num[3][0]/num[3][1]==num[3][2])
            sum++;
        return ;
    }
    else if(step==3)
	{
        if(num[0][0]+num[0][1]!=num[0][2])
            return ;
    }
    else if(step==6)
	{
        if(num[1][0]-num[1][1]!=num[1][2])
            return ;
    }
    else if(step==9)
	{
        if(num[2][0]*num[2][1]!=num[2][2])
            return ;
    }
    for(int i=1;i<=13;i++)
	{
 
        if(!vis[i])
		{
            num[x][y]=i;
            vis[i]=1;
            dfs(step+1);
            vis[i]=0;
        }
    }
}
int main()
{
	dfs(0);
	printf("%d\n",sum);
}

答案：64

题目标题: 排它平方数

小明正看着 203879 这个数字发呆。

原来，203879 * 203879 = 41566646641

这有什么神奇呢？仔细观察，203879 是个6位数，并且它的每个数位上的数字都是不同的，并且它平方后的所有数位上都不出现组成它自身的数字。

具有这样特点的6位数还有一个，请你找出它！

再归纳一下筛选要求：
1. 6位正整数
2. 每个数位上的数字不同
3. 其平方数的每个数位不含原数字的任何组成数位

答案是一个6位的正整数。

请通过浏览器提交答案。

注意：只提交另一6位数，题中已经给出的这个不要提交。

注意：不要书写其它的内容（比如：说明性的文字）。

思路：暴力循环

答案：639172

标题: 颠倒的价牌

小李的店里专卖其它店中下架的样品电视机，可称为：样品电视专卖店。

其标价都是4位数字（即千元不等）。

小李为了标价清晰、方便，使用了预制的类似数码管的标价签，只要用颜色笔涂数字就可以了（参见p1.jpg）。

这种价牌有个特点，对一些数字，倒过来看也是合理的数字。如：1 2 5 6 8 9 0 都可以。
这样一来，如果牌子挂倒了，有可能完全变成了另一个价格，比如：1958 倒着挂就是：8561，差了几千元啊!! 

当然，多数情况不能倒读，比如，1110 就不能倒过来，因为0不能作为开始数字。

有一天，悲剧终于发生了。某个店员不小心把店里的某两个价格牌给挂倒了。并且这两个价格牌的电视机都卖出去了!

庆幸的是价格出入不大，其中一个价牌赔了2百多，另一个价牌却赚了8百多，综合起来，反而多赚了558元。

请根据这些信息计算：赔钱的那个价牌正确的价格应该是多少？

答案是一个4位的整数，请通过浏览器直接提交该数字。

注意：不要提交解答过程，或其它辅助说明类的内容。

思路：循环，注意69的变化即可

答案：9088

标题：逆波兰表达式

正常的表达式称为中缀表达式，运算符在中间，主要是给人阅读的，机器求解并不方便。

例如：3 + 5 * (2 + 6) - 1

而且，常常需要用括号来改变运算次序。

相反，如果使用逆波兰表达式（前缀表达式）表示，上面的算式则表示为：

- + 3 * 5 + 2 6 1

不再需要括号，机器可以用递归的方法很方便地求解。

为了简便，我们假设：

1. 只有 + - * 三种运算符
2. 每个运算数都是一个小于10的非负整数

下面的程序对一个逆波兰表示串进行求值。
其返回值为一个结构：其中第一元素表示求值结果，第二个元素表示它已解析的字符数。

struct EV
{
	int result;  //计算结果 
	int n;       //消耗掉的字符数 
};

struct EV evaluate(char* x)
{
	struct EV ev = {0,0};
	struct EV v1;
	struct EV v2;

	if(*x==0) return ev;
	
	if(x[0]>='0' && x[0]<='9'){
		ev.result = x[0]-'0';
		ev.n = 1;
		return ev;
	}
	
	v1 = evaluate(x+1);
	v2 = _____________________________;  //填空位置
	
	if(x[0]=='+') ev.result = v1.result + v2.result;
	if(x[0]=='*') ev.result = v1.result * v2.result;
	if(x[0]=='-') ev.result = v1.result - v2.result;
	ev.n = 1+v1.n+v2.n;

	return ev;
}

请分析代码逻辑，并推测划线处的代码，通过网页提交。

注意：仅把缺少的代码作为答案，千万不要填写多余的代码、符号或说明文字！！

答案：evluate(x+v.n+1);

7-1 买不到的数目(qdulq) （30 分）

买不到的数目

小明开了一家糖果店。他别出心裁：把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。

小朋友来买糖的时候，他就用这两种包装来组合。当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。

你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。

本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式

两个正整数，表示每种包装中糖的颗数(都不多于1000)

输出格式

一个正整数，表示最大不能买到的糖数

样例输入1

4 7

样例输出1

样例输入2

3 5

样例输出2

资源约定：

峰值内存消耗 < 64M

CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0

注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。

注意: 所有依赖的函数必须明确地在源文件中 #include ，不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

思路：找规律

代码：

#include<iostream>
using namespace std;
int main()
{
	int a,b;
	scanf("%d %d",&a,&b);
	printf("%d",a*b-a-b);
}

7-2 大臣的旅费(qdulq) （40 分）

问题描述

很久以前，T王国空前繁荣。为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。

J是T国重要大臣，他巡查于各大城市之间，体察民情。所以，从一个城市马不停蹄地到另一个城市成了J最常做的事情。他有一个钱袋，用于存放往来城市间的路费。

聪明的J发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第x千米到第x+1千米这一千米中（x是整数），他花费的路费是x+10这么多。也就是说走1千米花费11，走2千米要花费23。

J大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入格式

输入的第一行包含一个整数n，表示包括首都在内的T王国的城市数

城市从1开始依次编号，1号城市为首都。

接下来n-1行，描述T国的高速路（T国的高速路一定是n-1条）

每行三个整数Pi, Qi, Di，表示城市Pi和城市Qi之间有一条高速路，长度为Di千米。

输出格式

输出一个整数，表示大臣J最多花费的路费是多少。

样例输入1

样例输出1

输出说明

大臣J从城市4到城市5要花费135的路费。

根据资源限制尽可能考虑支持更大的数据规模。

资源约定：

峰值内存消耗 < 64M

CPU消耗 < 5000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。注意: 所有依赖的函数必须明确地在源文件中 #include ，不能通过工程设置而省略常用头文件。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。注意：不要使用package语句。不要使用jdk1.6及以上版本的特性。注意：主类的名字必须是：Main，否则按无效代码处理。

提交时，注意选择所期望的编译器类型。

作者: happy

单位: 青岛大学

时间限制: 5000 ms

内存限制: 256 MB

代码长度限制: 16 KB

思路：求树的直径，并用向量数组，用数组会超时。

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring> 
using namespace std;
#define maxn 100005
int vis[maxn];
int va[maxn];
vector<int>node[maxn];
vector<int>edge[maxn];
void dfs(int k)
{
	vis[k] = 1;
	for(int i = 0; i < node[k].size(); i ++)
	{
		if(!vis[node[k][i]]&&edge[k][i]>0)
		{
			va[node[k][i]] = va[k] + edge[k][i];
			dfs(node[k][i]);
		}
	}	
}
int main()
{
	int n;
	scanf("%d",&n);
	for(int i = 1; i < n; i ++)
	{
		int a,b,c;
		scanf("%d %d %d",&a,&b,&c); 
		node[a].push_back(b);
		node[b].push_back(a);
		edge[a].push_back(c);
		edge[b].push_back(c);
	}
	dfs(1);
	int index = 1;
	int m = 0;
	for(int i = 1; i <= n; i ++)
	{
		if(va[i]>m)
		{
			index = i;
			m = va[i];
		} 
	}
	memset(vis,0,sizeof vis);
	memset(va,0,sizeof va);
	dfs(index);
	index = 1;
	m = 0;
	for(int i = 1; i <= n; i ++)
	{
		if(va[i]>m)
		{
			index = i;
			m = va[i];
		} 
	}
	int sum = m*10+(1+m)*m/2;
	printf("%d",sum); 
}

7-3 剪格子(qdulq) （30 分）

标题：剪格子

如图p1.jpg所示，3 x 3 的格子中填写了一些整数。

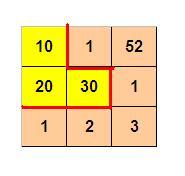
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是60。

本题的要求就是请你编程判定：对给定的m x n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 0

程序输入输出格式要求：

程序先读入两个整数 m n 用空格分割 (m,n<10)

表示表格的宽度和高度

接下来是n行，每行m个正整数，用空格分开。每个整数不大于10000

程序输出：

在所有解中，包含左上角的分割区可能包含的最小的格子数目。

例如：

用户输入：

则程序输出：

再例如：

用户输入：

则程序输出：

(参见p2.jpg)

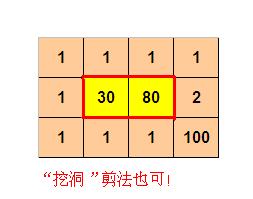
资源约定：

峰值内存消耗（含虚拟机） < 64M

CPU消耗 < 5000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意：不要使用package语句。不要使用jdk1.6及以上版本的特性。

注意：主类的名字必须是：Main，否则按无效代码处理。

注意: main函数需要返回0

注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。

注意: 所有依赖的函数必须明确地在源文件中 #include ，不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

思路：dfs

代码：

#include <iostream>
using namespace std;
int a[10][10];
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};
bool isv[10][10];
int M,N,SUM;
bool judge(int x,int y,int num)
{
    if( x<1 || y<1 || x>N || y>M||isv[x][y]) 
		return 1;
    if( num + a[x][y] > SUM/2 )    //走这一步超过了和的1半 
        return 1;
    return 0;
}
int dfs(int x,int y,int num)
{
    if(num==SUM/2)
	{
        return 1;
    }
    for(int i=0;i<4;i++)
	{
        int nx = x + dx[i];
        int ny = y + dy[i];
        if( judge(nx,ny,num) )    //判断 
            continue;
        //下一步可以走
        isv[nx][ny] = true;
        int res = dfs(nx,ny,num+a[nx][ny]);
        if(res)    //产生结果，直接返回 
            return res+1;
        isv[nx][ny] = false;
    }
    return 0; 
}
int main()
{
		 
        scanf("%d %d",&N,&M); 
        for(int i=1;i<=N;i++)
            for(int j=1;j<=M;j++)
			{
                cin>>a[i][j];
                SUM += a[i][j];
            }
        if( SUM%2 )
		{    //和是奇数一定不可以 
            cout<<0<<endl;
        }
        else
		{    //和是偶数继续判断
            isv[1][1] = true;
            cout<<dfs(1,1,a[1][1])<<endl;
        }
}