fasttext做文本分类阶段性学习总结
预备知识
logistic回归与softmax回归
logistic回归
logistic回归是一种有监督的统计学习方法,主要用于对样本进行分类。对于监督学习问题而言,常常会给定数据以及数据对应的标签值。比如我们可以通过logistic回归算法得到一个映射函数 f:X→y ,其中 X 为特征向量,X={x0,x1,x2,…,xn},y 为预测的结果。在逻辑回归这里,标签 y为一个离散值(y0,y1,y2,…,yn)。
sigmoid函数
如果希望分类器输出值在0和1之间: 0 ≤ h θ ( x ) ≤ 0 0≤h_{θ}(x)≤0 0≤hθ(x)≤0 ==> 引入 h θ ( x ) = g ( θ T x ) h_{θ}(x)=g(θ^{T}x) hθ(x)=g(θTx) ,其中: g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,则: h θ ( x ) = 1 1 + e − θ T x h_{θ}(x)=\frac{1}{1+e^{-θ^{T}x}} hθ(x)=1+e−θTx1
θ θ θ 为特征向量X={x0,x1,x2,…,xn}的参数,它是一个n维向量(在线性回归和logistic回归中, θ θ θ称参数,在神经网络中, θ θ θ称模型的权重)。
g ( z ) g(z) g(z)称为sigmoid函数(或称logistic函数),它的函数图像如下:
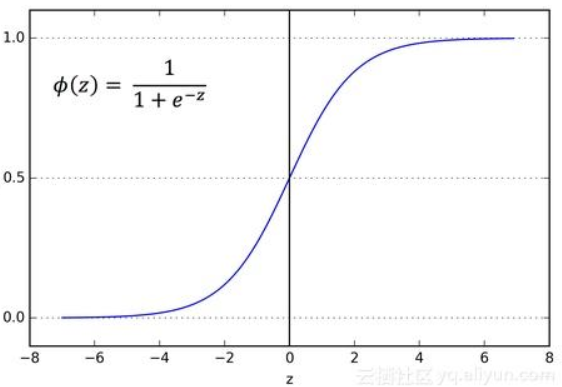
根据图像可知,sigmoid函数具有如下特点:
- 当z为0左右时,函数值为0.5左右
- z越大于0时,函数值越大于0.5越收敛于1
- z越小于0时,函数值越小于0.5越收敛于0
因此可以将sigmoid函数作为二分类问题的假设函数,将其转化为概率问题描述就变成了:
- 当 θ T x ≥ 0 θ^{T}x≥0 θTx≥0 时,样本标记的类型为某一类型的概率会等于或高于0.5,即: h θ ( x ) ≥ 0.5 h_{θ}(x)≥0.5 hθ(x)≥0.5 ==> 预测 y = 1 y=1 y=1
- 当 θ T x < 0 θ^{T}x<0 θTx<0 时,样本标记的类型为某一类型的概率会低于0.5,即: h θ ( x ) < 0.5 h_{θ}(x)<0.5 hθ(x)<0.5 ==> 预测 y = 0 y=0 y=0
则针对二分类问题而言: p ( y = 0 ∣ x ; θ ) + p ( y = 1 ∣ x ; θ ) = 1 p(y=0|x;θ)+p(y=1|x;θ)=1 p(y=0∣x;θ)+p(y=1∣x;θ)=1
决策边界
sigmoid函数 h θ ( x ) = g ( θ T x ) h_{θ}(x)=g(θ^{T}x) hθ(x)=g(θTx) 中,方程 θ T x = 0 θ^{T}x=0 θTx=0 表示决策边界,在二分类问题中,决策边界一边为A类,另一边划分为B类。如下例所示:
【例1】设 h θ ( x ) = g ( θ T x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_{θ}(x)=g(θ^{T}x)=g(θ_{0}+θ_{1}x_{1}+θ_{2}x_{2}) hθ(x)=g(θTx)=g(θ0+θ1x1+θ2x2) 其中 θ = ( − 3 1 1 ) θ=\begin{pmatrix}-3\\1 \\1\end{pmatrix} θ=⎝⎛−311⎠⎞
则: h θ ( x ) = g ( θ T x ) = g ( − 3 + x 1 + x 2 ) h_{θ}(x)=g(θ^{T}x)=g(-3+x_{1}+x_{2}) hθ(x)=g(θTx)=g(−3+x1+x2) , 当 θ T x = 0 θ^{T}x=0 θTx=0 时,即决策边界为: − 3 + x 1 + x 2 = 0 -3+x_{1}+x_{2}=0 −3+x1+x2=0,如下图所示:
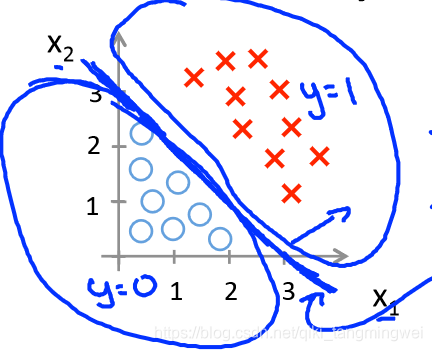
图中加粗的蓝线即为 决策边界,可看出,在给定合适的 θ θ θ 参数前提下,模型能很好得对数据集做二分类。那么如何能自动得出合适的 θ θ θ 参数呢?可通过代价函数实现。
代价函数
代价函数又称“平方误差函数”,它是解决回归问题的常用手段,它通常是一个 凸函数(碗状)具有全局最优解(如正态函数)。
代价函数的功能就是用来拟合logistic回归模型参数 θ θ θ
对于sigmoid函数 g ( θ T x ) = 1 1 + e − θ T x g(θ^{T}x)=\frac{1}{1+e^{-θ^{T}x}} g(θTx)=1+e−θTx1, 需要为它找到一个代价函数 J ( θ ) J(θ) J(θ),使得 J ( θ ) J(θ) J(θ)为一个完整的凸函数,方便收敛以找到全局最优值(这里是最小值)。则定义: C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) y = 1 − l o g ( 1 − h θ ( x ) ) y = 0 Cost(h_{θ}(x),y)=\left\{ \begin{array}{rcl} -log(h_{θ}(x)) & & {y=1}\\ -log(1-h_{θ}(x)) & & {y=0}\\ \end{array} \right. Cost(hθ(x),y)={ −log(hθ(x))−log(1−hθ(x))y=1y=0
函数曲线如下图所示:
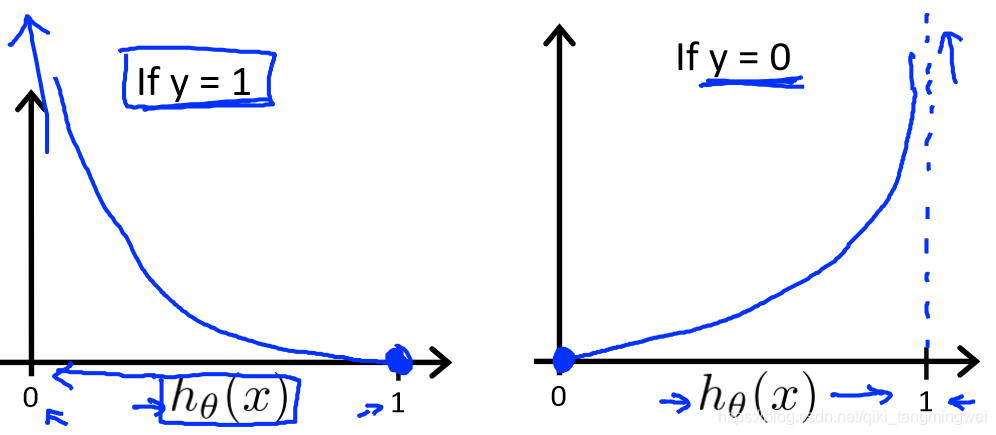
- 【 i f if if y = 1 y=1 y=1 】 当 h θ ( x ) h_{θ}(x) hθ(x) -> 0 , C o s t Cost Cost -> ∞ ∞ ∞,则预测 p ( y = 1 ∣ x ; θ ) = 0 p(y=1|x;θ)=0 p(y=1∣x;θ)=0
- 【 i f if if y = 0 y=0 y=0 】 当 h θ ( x ) h_{θ}(x) hθ(x) -> 1 , C o s t Cost Cost -> ∞ ∞ ∞,则预测 p ( y = 0 ∣ x ; θ ) = 0 p(y=0|x;θ)=0 p(y=0∣x;θ)=0
合成一个表达式,则logistic回归代价函数表达式如下: C o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) Cost(h_{θ}(x),y)=-ylog(h_{θ}(x))-(1-y)log(1-h_{θ}(x)) Cost(hθ(x),y)





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








