每周一算法：无向图的最小环

题目链接

观光之旅

题目描述

给定一张无向图，求图中一个至少包含 $3$ 个点的环，环上的节点不重复，并且环上的边的长度之和最小。

该问题称为无向图的最小环问题。

你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。

输入格式

第一行包含两个整数 $N$ 和 $M$，表示无向图有 $N$ 个点，$M$ 条边。

接下来 $M$ 行，每行包含三个整数 $u，v，l$，表示点 $u$ 和点 $v$ 之间有一条边，边长为 $l$。

输出格式

输出占一行，包含最小环的所有节点（按顺序输出），如果不存在则输出 No solution.。

样例 #1

样例输入 #1

5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20

样例输出 #1

1 3 5 2

提示

【数据范围】

$1\le N\le 100$,
$1\le M\le 10000$,
$1\le l<500$

算法思想

根据题目描述，求的是无向图中的最小环，要求环中至少包含 $3$ 个节点，且环上的节点不重复。当边权都为正数式，最小环中的节点一定不会重复，否则就不是最小环了，如下图所示。

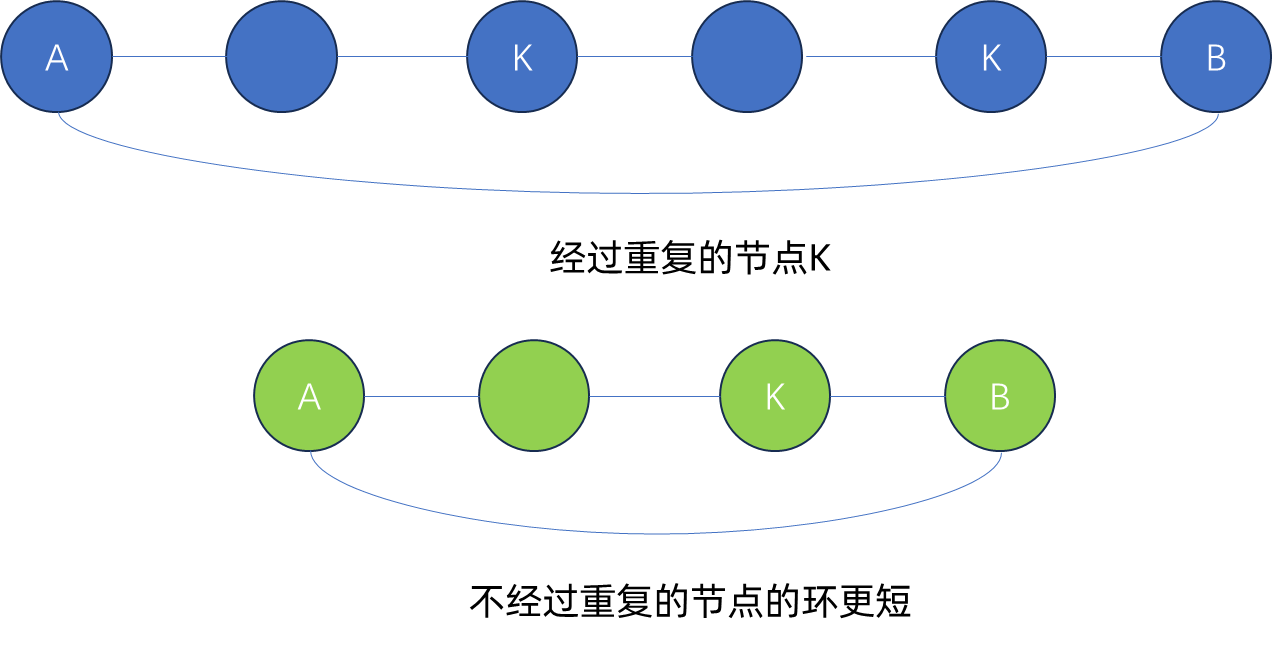
求最小环的长度

无向图的最小环问题可以使用「Floyd」算法解决。基本思想是：

• 当外层循环$k$刚开始时，$d[i,j]$保存着从节点$i$到$j$经过编号不超过$k-1$的最短路径长度
• 此时，如果引入新节点$k$构成了环，那么环的长度为$d[i,j]+g[j][k]+g[k][i]$，如下图所示：
  
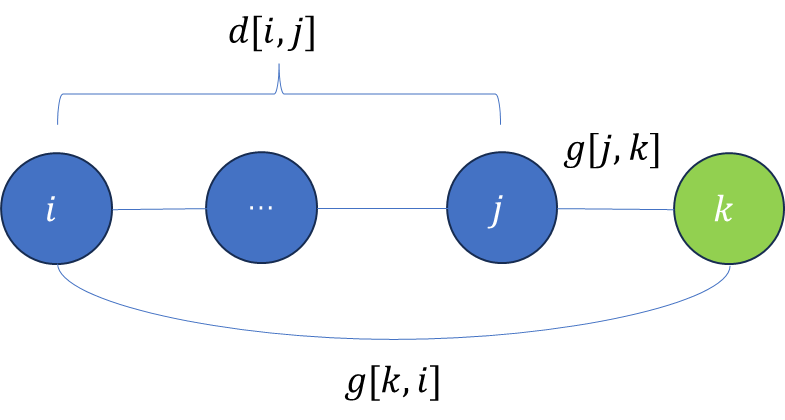
  那么，min{d[i,j]+g[j][k]+g[k][i]}min\{d[i,j]+g[j][k]+g[k][i]\}min{d[i,j]+g[j][k]+g[k][i]}，其中$1\le i<j<k$，就是满足以下两个条件的最小环长度：
  • 由编号不超过$k$的节点构成
  • 经过节点$k$

从$1\sim n$枚举$k$，取上式的最小值，就可以得到整张图的最小环长度。

求最小环上的节点

除了计算最小环之外，题目还要求记录最小环的上所有节点。当更新最小环时，环上的节点包含$i$、$i$到$j$之间最短路上的节点，以及$i$和$k$。那么如何得到$i$到$j$之间最短路上的节点

使用Floyd算法计算最短路时，当$d[i][j]>d[i][k]+d[k][j]$时，可以更新节点$i$到$j$的最短路，同时记录节点$i$到$j$的最短路是经过$k$点中转得到的，不妨记$pos[i,j]=k$。

那么经过节点$i$到$j$的最短路径的可以分成两个部分：

• 节点$i$到$k$的最短路
• 节点$k$到$j$的最短路

可以通过递归的方式，分别获取这两部分经过的节点。

时间复杂度

Floyd算法内可以同时求最小环和最短路，因此时间复杂度为$O(n^3)$。

代码实现

#include <bits/stdc++.h>
using namespace std;
const int N = 105, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], d[N][N];
int pos[N][N];//pos[i][j]表示i和j最短路经过k点中转
vector<int> path; //保存最小环路径
void get_path(int i, int j)
{
    if(pos[i][j] == 0) return; //i和j之间不存在中转点
    int k = pos[i][j]; //k是i和j最最短路的中转点
    get_path(i, k); //递归后取i-k最短路上的节点
    path.push_back(k);
    get_path(k, j); //递归后取k-j最短路上的节点
}
int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g); //初始化邻接矩阵
    for(int i = 1; i <= n; i ++) g[i][i] = 0;
    while (m -- )
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c); //无向图，可能存在重边
    }
    int ans = INF;
    memcpy(d, g, sizeof d); //初始化最短路
    for(int k = 1; k <= n; k ++)
    {
        //计算由编号不超过k的节点构成的最小环
        for(int i = 1; i < k; i ++) //枚举环中的点
            for(int j = i + 1; j < k; j ++)
            {
                if((long long)d[i][j] + g[j][k] + g[k][i] < ans) //出现更小的环
                {
                    ans = d[i][j] + g[j][k] + g[k][i];
                    path.clear(); //清除之前的最小环路径
                    path.push_back(k); //k-i-最短路路径-j
                    path.push_back(i);
                    get_path(i, j);//获取i-j最短路径上的节点
                    path.push_back(j);
                }
            }
        //计算最短路
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                if(d[i][j] > d[i][k] + d[k][j])
                {
                    d[i][j] = d[i][k] + d[k][j];
                    pos[i][j] =k; //记录最短路中转点
                }
    }
    if(ans == INF) puts("No solution.");
    else //存在最小环
    {
        for(int i : path) cout << i << " ";
    }
}