蓝桥杯青少组python：第十二届国赛

选择题

1、设s="Hi LanQiao"，运行一下哪个选项代码可以输出"LanQiao"子串（）

• A、print(S[-7:])
• B、print(s[-6:-1])
• C、print(s[-7:0])
• D、print(s[-7:0])

2、已知a=2021.0529，运行一下代码选项可以输出2021.05（）

• A、print("{2f}".format(a))
• B、print("{:.2f}".format(a))
• C、print("{2}".format(a))
• D、print("{.2f}".format(a))

3、已知pi=3.1415924，运行print(round(pi),round(pi,2))，输出结果是（）

• A、3 3.14
• B、2 4
• C、3 6.18
• D、3.14 3

4、运行以下程序，输出的结果是（）

d = {"Beijing":"China", "Washington":"America", "Ottawa":"Canadian" }
print(max(d), min(d))

• A、Washington Ottawa
• B、Canadian China
• C、America China
• D、Washington Beijing

5、如果p=ord("b")，运行print(p,chr((p+3)%26+p))语句，输出结果是（）：

• A、66 D
• B、66 S
• C、98 y
• D、98 e

操作题

T1、最大数

给定$N$个数字（包含整数和小数），找到$N$个数中最大的数字。

输入描述

输入$N$个数字（$N>2$），且$N$个数字之间以英文逗号隔开。

输出描述

输出$N$个数字中最大的数字。

输入样例

4,3,9,10

输出样例

10

代码实现

a = eval(input())
print(max(a))

T2、质因数

质数是一个大于$1$的自然数，且除了$1$和它本身外，不能被其他自然数整除的数。最小的质数是$2$，$1$不是质数。

合数，一个正整数，如果除$1$和它本身以外，还能被其他正整数整除，叫合数。如$6$是合数，除了$1$和$6$以外，还能被$2$和$3$整除。

分解质因数，每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数，把一个合数用质因数相乘的形式表示出来，叫做分解质因数（分解质因数只针对合数）。如合数$12=2\times 2\times 3$。

分解质因数的方法是先用这个合数的最小质因数去除这个合数，结果若是一个质数就不再除下去；若是一个合数就继续按原来的方法从最小质因数除起，直至最后除得的结果是一个质数。

例如：合数$18$分解质因数，首先用最小质因数$2$去除，除后结果为合数$9$，继续用最小质因数$3$去除，除后结果为质数$3$，就不再除下去。所以$18$的质因数为$2$、$3$、$3$，故质因数的个数为$3$。

给定一个合数$N$，将$N$分解质因数后，输出其质因数个数。

输入描述

输入一个合数$N$。

输出描述

将$N$分解质因数后，输出质因数个数

输入样例

18

输出样例

3

代码实现

n = int(input())
ans = 0
i = 2
while n > 1:
	while n % i == 0:
		n = n / i
		ans += 1
	i += 1
print(ans)

T3、数字字符串

给定一个含有字母和数字的字符串，输出此字符串中最长的数字子串的长度。

如：字符串”a2a22d“，最长的数字子串为"22"，长度为$2$，故输出$2$。

字符串"lq12h567j765"，最长的数字子"567"和"765"，长度都为$3$，故输出$3$。

输入描述

输入一个候有字母和数字的字特串（$5<字等串长度<101$）

输出描述

输出此字符串中最长的数字子串的长度。

输入样例

a2a22d

输出样例

2

代码实现

s = input()
ans = 0
n = 0 # 记录数字子串的长度
for x in s:
    if x >= "0" and x <= "9": # 如果是数字
        n += 1
    else:
        ans = max(ans, n)
        n = 0
print(ans)

T4、数字字符串

质数是一个大于$1$的自然数，且除了$1$和它本身外，不能被其他自然数整除的数。最小的质数是$2$，$1$不是质数。

大于$2$的偶数有一个特点，任意一个大于$2$的偶数可以由一对质数相加得到，但有的偶数不知由一对这样的质数对。如偶数$6$，有一对质数相加得$6$，为$(3,3)$；如偶数$14$，有两对质数相加得$14$，分别是$(3,11),(7,7)$。

编程实现，给定一个大于$2$的偶数，在所有满足“任意一个大于$2$的偶数可以由两个质数相加得到”这个特点的质数对中，找出两个质数差值最小的一对，并将差值输出。（差值为大数减小数的值，两个质数相等时差值为$0$）。

例如，偶数$16$，满居特点的质数对有$(5,11)$和$(3,13)$，差值最小的一对是$(5,11)$，$11$减$5$，差值为$6$。

输入描述

输入一个大于$2$得偶数$N$。

输出描述

输出满足“任意一个大于$2$的偶数可以由两个质数相加得到”这个特点的质数对中，差值最小的一对的差值。

输入样例

16

输出样例

6

代码实现

# 判断质数
def is_prime(n):
    for i in range(2, n):
        if n % i == 0:
            return False
    return True
n = int(input())
ans = n
# 枚举加数
for i in range(2, n // 2 + 1):
    if is_prime(i) and is_prime(n - i):
        ans = min(ans, n - i - i)
print(ans)

T5、金箍棒

孙悟空的金箍棒可以变高也可以变矮还可以变出多个金箍棒。这天孙悟空无聊变出了$N$个长短不一的金箍棒，这些金箍棒之间相互吵闹，攀比谁高。当孙悟空每次手指其中一个金箍棒时，这个金箍棒高度不变，其他的金箍棒高度都会增加$1$。

只有当所有金箍棒高度都一样时，他们之间才不相互吵闹，也不会再增加高度，保持静止。分别给定$N$个金箍棒的初始高度，请你帮助孙悟空计算一下至少手指几次可以让$N$个金箍棒高度都一样。

例如，有$3$个金箍棒，初始高度分别为$2,3,4$。

• 第一次手指第三个金箍棒，第三个金箍棒高度不变，第一和第二个金箍棒高度分别增加$1$，变为$3,4,4$；
• 第二次手指第二个金箍棒，第二个金箍棒高度不变，第一和第三个金箍棒高度分别增加$1$，变为$4,4,5$；
• 第三次手指第三个金箍棒，第三个金箍棒高度不变，第一和第二个金箍棒高度分别增加$1$，变为$5,5,5$；

这时$3$个金箍棒的高度都为$5$，手指$3$次后金箍棒高度一样。所以至少手指$3$次才能使金箍棒高度都一样。

输入描述

输入$N$个非全部相等的正整数（$N$个数不全部相等，$2<N<31$），且之间以英文逗号隔开，分别表示$N$个金箍棒的初始高度。

输出描述

输出一个正整数，表示至少手指几次才能使金箍棒高度都一样。

输入样例

2,3,4

输出样例

3

解题思路

• 只要所有金箍棒高度不相等
  • 就需要指定最高的金箍棒，然后让其它金箍棒高度增加$1$。
  • 记录操作次数

代码实现

a = list(eval(input()))
ans = 0
# 只要最高和最矮不相等
while max(a) != min(a):
    ans += 1
    # 指向最长的金箍棒，其它金箍棒高度增加1
    idx = a.index(max(a))
    for i in range(len(a)):
        if idx != i:
            a[i] += 1 # 高度增加1
print(ans)

T6、花卉

六月一日是国际儿童节，小蓝的学校为迎接儿童节要在学校的一块正方形空地上使用不同颜色的花卉摆放图案。为了摆放的更精准，图案更漂亮，小蓝把这块正方形空地同比例缩小将其画在纸上，并平分成$100\times 100$的方格，每个方格的坐标点为$(1,1)...(100,100)$，如下图所示。

首先在指定坐标的方格内放置红色的花卉（每个方格放一盆）。完成后，找出最多有多少盆红色花卉在同一条直线上。（同一直线包含同一列。同一行，同一对角线，红色花卉可以连续也可以不连续）

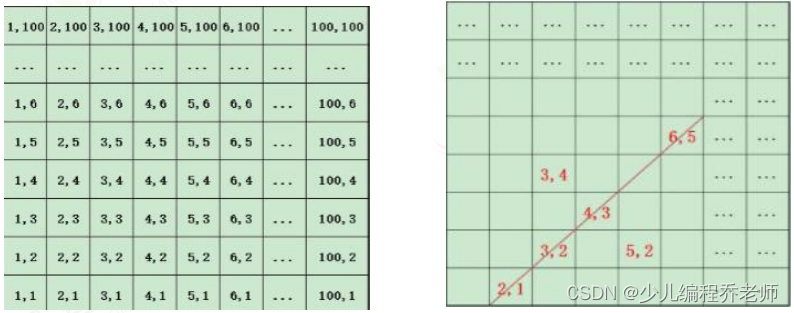
如：随机指定坐标$(2,1),(3,2),(5,2),(4,3),(3,4),(6,5)$的方格内放置红色的花卉，其中最多的红色花卉在同一条直线上的坐标点为$(2,1),(3,2),(4,3),(6,5)$，故最多有$4$盆红色的花卉在同一条直线上。

输入描述

输入$n$对正整数，每一对正整数之间以一个空格隔开，代表放置红色花卉的方格位置。

每对正整数中的两个数字以英文逗号隔开。

输出描述

输出最多有多少盆红色花卉在同一条直线上

输入样例

2,1 3,2 5,2 4,3 3,4 6,5

输出样例

4

解题思路

• 使用二维列表保存每个方格的状态，输入花卉的行列后，将列表对应位置标记为1
• 分别求行、列，以及每条对角线上拥有花卉数的最大值，结果为这三者的最大值

代码实现

ls = input().split();
# 初始化101 * 101的二维列表
g = [[0] * 101 for _ in range(101)]
sx = sy = 100 #起始行列
ex = ey = 1 #结束行列
points = []
for s in ls:
    x, y = map(int, s.split(','))
    g[x][y] = 1
    points.append((x, y))
    sx = min(sx, x)
    sy = min(sy, y)
    ex = max(ex, x)
    ey = max(ey, y)
# 行的最大值
ans = 0
for i in range(sx, ex + 1):
    t = 0
    for j in range(sy, ey + 1):
        t += g[i][j]
    ans = max(ans, t)
# 列的最大值
for i in range(sy, ey + 1):
    t = 0
    for j in range(sx, ex + 1):
        t += g[j][i]
    ans = max(ans, t)
# 右下对角线↘
for i in range(sx, ex + 1):
    for j in range(sy, ey + 1):
        x, y, t, k = i, j, 0, 1
        while x + k - 1 <= ex and y + k - 1 <= ey:
            t += g[x][y]
            x += 1
            y += 1
        ans = max(ans, t)

# 右上对角线↗
for i in range(sx, ex + 1):
    for j in range(sy, ey + 1):
        x, y, t, k = i, j, 0, 1
        while x - k + 1 >= sx and y + k - 1 <= ey:
            t += g[x][y]
            x -= 1
            y += 1
        ans = max(ans, t)
print(ans)