监督学习之一般最小二乘法

定义

线性回归通过拟合一个系数为 W = (W1, W2, ...., Wn) 的线性模型，以最小化观测目标与预测目标之间的残差平方和。这种线性拟合方法叫做一般最小二乘法。

在数学上，它可以解决以下形式的问题：

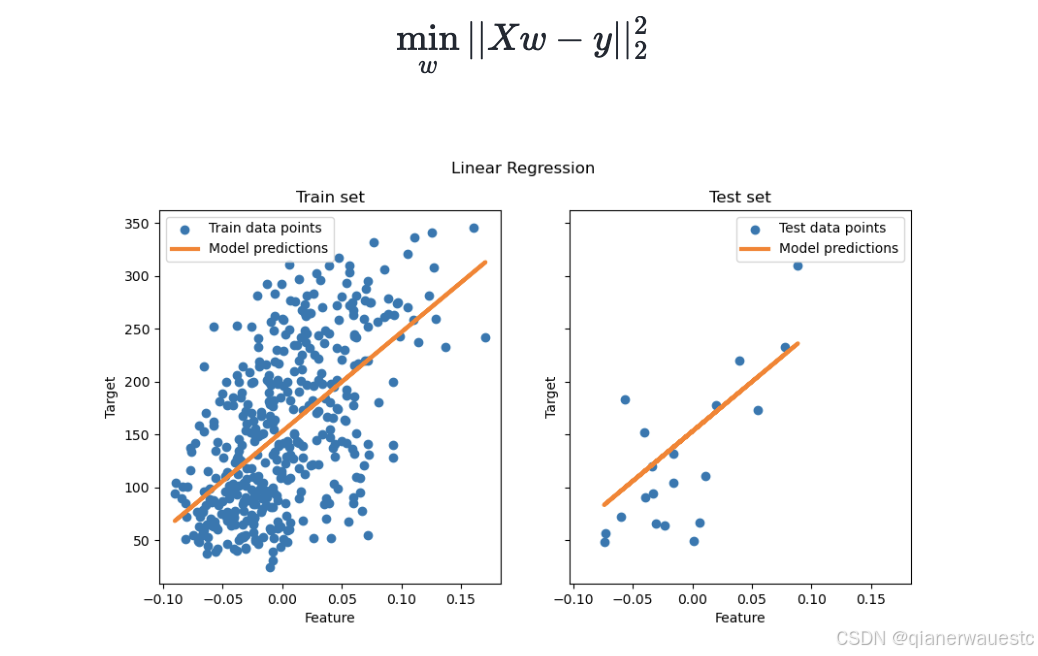
实现

线性回归将在该拟合方法中使用数组 X、y，并在其 coef_ 成员中存储线性模型的系数。

from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
reg.coef_
array([0.5, 0.5])

缺点

一般最小二乘法的系数估计依赖于特征的独立性。当特征相互关联且设计矩阵 X 的列具有近似线性相关性时，设计矩阵就会变得接近奇异，因此最小二乘估计值就会对观测目标中的随机误差高度敏感，从而产生较大的方差。例如，在没有实验设计的情况下收集数据时，就会出现这种多重共线性的情况。

案例

来源：https://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html#sphx-glr-auto-examples-linear-model-plot-ols-py