Nearest Common Ancestors
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 14078 | Accepted: 7510 |
Description
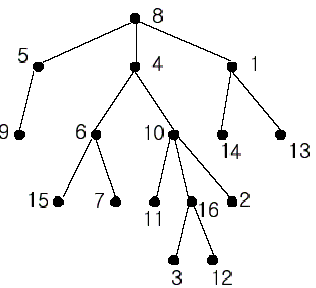
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
Output
Sample Input
2 16 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7 5 2 3 3 4 3 1 1 5 3 5
Sample Output
4 3
Source
在线算法 倍增法
每次询问O(logN)
d[i] 表示 i节点的深度, p[i,j] 表示 i 的 2^j 倍祖先
那么就有一个递推式子 p[i,j]=p[p[i,j-1],j-1]
这样子一个O(NlogN)的预处理求出每个节点的 2^k 的祖先
然后对于每一个询问的点对a, b的最近公共祖先就是:
先判断是否 d[a] > d[b] ,如果是的话就交换一下(保证 a 的深度小于 b 方便下面的操作)然后把b 调到与a 同深度, 同深度以后再把a, b 同时往上调(dec(j)) 调到有一个最小的j 满足p[a,j]!=p[b,j] (a b 是在不断更新的), 最后再把 a, b 往上调 (a=p[a,0], b=p[b,0]) 一个一个向上调直到a = b, 这时 a or b 就是他们的最近公共祖先
http://poj.org/problem?id=1330
【分析】
倍增法求LCA的大体思路:
首先确定深度d[i],表示i到根节点的距离或者说是深度。
p[i,j]表示i向上的第2^j个祖先,则p[i,j+1]:=p[p[i,j],j];
dfs求出d[i]和p[i,j]。
如果求的是x和y的lca。那么如果x=y,lca=x or y;
如果x和y的深度不同,则调整到同一深度,以便求lca。
x和y的深度相同了,就开始向上走,如果两个点同时走了相同的步数,走到了一个点,那么这个点就是lca,自己想象一下,这是显然的事。两个点最早到达的相同点不是lca是什么= =
结束。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
#define N 10010
#define M 20
int d[N],f[N][M];
vector<int>ch[N];
void dfs(int x){//求出所有结点深度
d[x]=d[f[x][0]]+1;
for(int i=1;i<M;i++)f[x][i]=f[f[x][i-1]][i-1];//倍增祖先
for(int i=ch[x].size()-1;i>=0;i--)
dfs(ch[x][i]);//遍历儿子
}
int lca(int x,int y){//求x,y最小公共祖先
if(d[x]<d[y])swap(x,y);//保证x的深度不小于y
int k=d[x]-d[y];
for(int i=0;i<M;i++)
if((1<<i)&k)
x=f[x][i];
if(x==y)return x;//x==y时为最小公共祖先
for(int i=M-1;i>=0;i--)
if(f[x][i]!=f[y][i]){
x=f[x][i];y=f[y][i];
}
return f[x][0];
}
int main(){
int T,n,i,x,y;
scanf("%d",&T);
while(T--){
scanf("%d",&n);
memset(d,0,sizeof(d));
memset(f,0,sizeof(f));
memset(ch,0,sizeof(ch));
for(i=1;i<n;i++){
scanf("%d%d",&x,&y);
ch[x].push_back(y);
f[y][0]=x;
}
for(i=1;i<=n;i++)
if(f[i][0]==0){//找到根遍历
dfs(i);break;
}
scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
return 0;
}





 本文介绍了一种高效算法——倍增法,用于解决寻找树中两节点的最近公共祖先(LCA)问题。通过预处理节点的深度及特定祖先信息,实现快速查询,适用于竞赛编程与实际工程项目。
本文介绍了一种高效算法——倍增法,用于解决寻找树中两节点的最近公共祖先(LCA)问题。通过预处理节点的深度及特定祖先信息,实现快速查询,适用于竞赛编程与实际工程项目。
















 407
407

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








