删除排序链表中的重复节点

1.基础问题
给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。
示例 :
输入: 1->1->2
输出: 1->2
2.算法
这里起初想法就是想着两个节点两个节点的比较以上述例子为例子。首先两个指针P和Q指向两个1，比较两个指针的值，发现相同;

此时将Q所在的这一个节点断开，P指向的节点不变，将Q指向下一节点继续比较：

直至Q指向链表末端：

/**
 * 链表节点定义
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
public class Solution83 {
	public ListNode deleteDuplicates(ListNode head) {
		//边界条件
		if(head==null ||head.next==null)
			return head;
		
		ListNode temp=head.next,pre=head;//前后节点
		while(temp!=null) {
		//前后节点进行判断，如果相等，则进行链表重链接操作
			if(temp.val==pre.val) {	
				pre.next=temp.next;
				temp.next=null;
				temp=pre.next;
			}
			else {
				temp=temp.next;
				pre=pre.next;
			}
		}	
		return head;
    }
}

现在这个比较简单，时间复杂度为O(N)，空间复杂度为O(1)，没有使用其他的空间。
3.问题升级
给定一个排序链表，删除所有含有重复数字的节点，只保留原始链表中 没有重复出现 的数字。
示例 1:
输入: 1->2->3->3->4->4->5
输出: 1->2->5
4.算法
在解决这个问题的时候，我就有了窗口滑动的想法，具体解释如下:
初始情况链表如下：

为了画图快点，节点之间的链接就没有画出来，Num是一个记录值，具体记录看步骤解释就知道了。
第一步：
比较P和Q，即窗口大小为2，当P和Q不相同时，Num=P.val=1；然后P和Q指向下一节点。（一直到P和Q的值相同的情形）

第二步：
此时P和Q相同，因此先删除P所在节点，然后P和Q一样指向下一节点。
相同时情况：

断开P现在节点，然后P,Q指向下一节点：(黄色节点表示这个节点已断开)

第三步：
这步是整个算法的判断核心，也是Num其作用的一步，即此时P和Q不同，但是根据题目要求来说，P现在所在的节点在上一步就应该删除掉，因此需要判断当P!=Q时，若P=Num，则此时的P也得断开。断开后，P和Q继续指向下一节点。

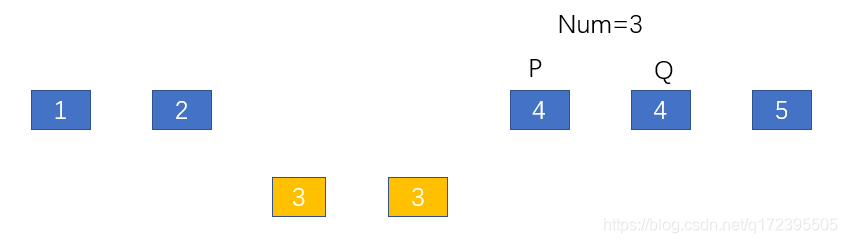
接着一直重复上述操作，直到Q指向链表末端。
代码如下：

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if(head==null ||head.next==null)
			return head;
		ListNode temp=head.next,next=head,newlist= new ListNode(0),newtemp=newlist;
		int num=Integer.MIN_VALUE;

		while(temp!=null) {
			if(temp.val==next.val) {	//滑动一个节点
				num=next.val;
				temp=temp.next;
				next=next.next;
                continue;
			}
			else if(temp.val!=next.val) {
			//判断是否与上一个窗口的最后一个链表节点相同
				if(next.val!=num) {	
					newtemp.next=next;
					newtemp=newtemp.next;

					num=next.val;   //滑动窗口
					next=next.next;
					temp=temp.next;

                    newtemp.next=null;//链表断开，否则链接会错误
				}
				else {
					next=temp;	//滑动窗口
					temp=temp.next;
				}
			}
		}
        if(temp==null&&next!=null) {
        	//判断是否与上一个窗口的最后一个链表节点相同
			if(next.val!=num) {
				newtemp.next=next;
				newtemp=newtemp.next;
				newtemp.next=null;
		}
		}
        return newlist.next;
	}
		
}

这样的算法时间复杂度也还是O（N），空间复杂度最大为O(N),最小为O（1）,我这里是用了一个新的链表来链接节点，因此空间复杂度会大一点。