【数据结构】旋转数组中的最小数字

  惯例，我们来看一下题目:

    把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个数递增排序的数组的一个旋转，输出旋转数组的最小元素，例如{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1.

 这个题最直观的解法根本没有任何难度，我们只需要遍历数组一次。就能够找出最小的元素。但是这样的题用这样就是0(n)的时间复杂度。

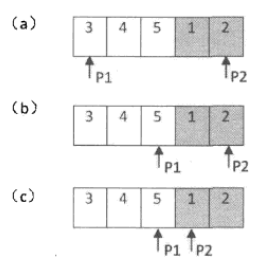
  那有没有什么优化的余地呢？关于查找我们我有许多的查找方法。二分查找无非不是这道题很好的一种诠释。不管这个数组怎么旋转，他任然是2个有序的系列。依然。我们画图举例。

对于二分查找依旧寻找中间值对两端的值进行比较，可以得到我们所要选取的范围区间，

a.当中间值大于左端，属左端的递增序列于那么范围将缩小到右端，小于将缩小到左端。

每次进行判断，都将会缩小所选取的范围值一半。当指向相邻元素时，第二个指针将会是最小值。

基于这个思路，我们将写出代码：

int Min(int *number,int length)
{
    if(numbers == NULL || length <= 0)
        cout<<"Invalid  parameters";
       
    int indexS = 0;
    int indexE = length - 1;
    int indexM = indexS;
    while(number[indexS] >= number[indexE])
    {
        if(1 == indexE - indexS)
        {
            indexM = indexE;
            break;
        }
        indexM = (indexS + (indexE - indexS)/2);
        if(number[indexM] >= number[indexS])
        {
            indexS = indexM;
        }
        else if(number[indexM] <= number[indexE])
        {
            indexE = indexM;
        }
    }
    return numbers[indexMid];
    
}

以上是解决正常的递增数组的方法，

但是如果遇上了{0,1,1,1,1}的旋转数组，我们需要对代码进行改进，当出现3个指针指向的值都相同时，我们不得不使用顺序查找来进行查找。

代码如下：

int Min(int *number,int length)
{
    if(numbers == NULL || length <= 0)
        cout<<"Invalid  parameters";
       
    int indexS = 0;
    int indexE = length - 1;
    int indexM = indexS;
    while(number[indexS] >= number[indexE])
    {
        if(1 == indexE - indexS)
        {
            indexM = indexE;
            break;
        }
        indexM = (indexS + (indexE - indexS)/2);
        
        if(number[indexM] = number[indexS] && number[indexM] == index[E])
        {
            return MinInorder(number,indexS,indexE)
        }
        if(number[indexM] >= number[indexS])
        {
            indexS = indexM;
        }
        else if(number[indexM] <= number[indexE])
        {
            indexE = indexM;
        }
    }
    return numbers[indexMid];
    
}

int Mainorder(int *number,int indexS,indexE)
{
    int result = number[indexS];
    for(int i = indexS + 1;i <= indexE;++i)
    {
        if(result >numbers[i])
            result = number[i];
    }
    return result;
}

这就是这个题目了。。需要考虑到一些东西

本文出自 “剩蛋君” 博客，转载请与作者联系！