深度学习 实验二 pytorch基础练习

1.1. 概念：张量

1.1.1定义

在深度学习的实践中，我们通常使用向量或矩阵运算来提高计算效率。比如w1x1+w2x2+⋯+wNxNw_1x_1 + w_2 x_2 +\cdots +w_N x_Nw1​x1​+w2​x2​+⋯+wN​xN​的计算可以用w⊤x\bm w^\top \bm xw⊤x来代替（其中w=[w1w2⋯wN]⊤，x=[x1x2⋯xN]⊤\bm w=[w_1 w_2 \cdots w_N]^\top，\bm x=[x_1 x_2 \cdots x_N]^\topw=[w1​w2​⋯wN​]⊤，x=[x1​x2​⋯xN​]⊤），这样可以充分利用计算机的并行计算能力，特别是利用GPU来实现高效矩阵运算。

在深度学习框架中，数据经常用张量(Tensor)的形式来存储。张量是矩阵的扩展与延伸，可以认为是高阶的矩阵。1阶张量为向量，2阶张量为矩阵。如果你对Numpy熟悉，那么张量是类似于Numpy的多维数组(ndarray)的概念，可以具有任意多的维度。

---

笔记

注意：这里的“维度”是“阶”的概念，和线性代数中向量的“维度”含义不同。

---

张量的大小可以用形状（shape）来描述。比如一个三维张量的形状是 [2,2,5][2, 2, 5][2,2,5]，表示每一维（也称为轴（axis））的元素的数量，即第0轴上元素数量是2，第1轴上元素数量是2，第2轴上的元素数量为5。

图1.5给出了3种纬度的张量可视化表示。

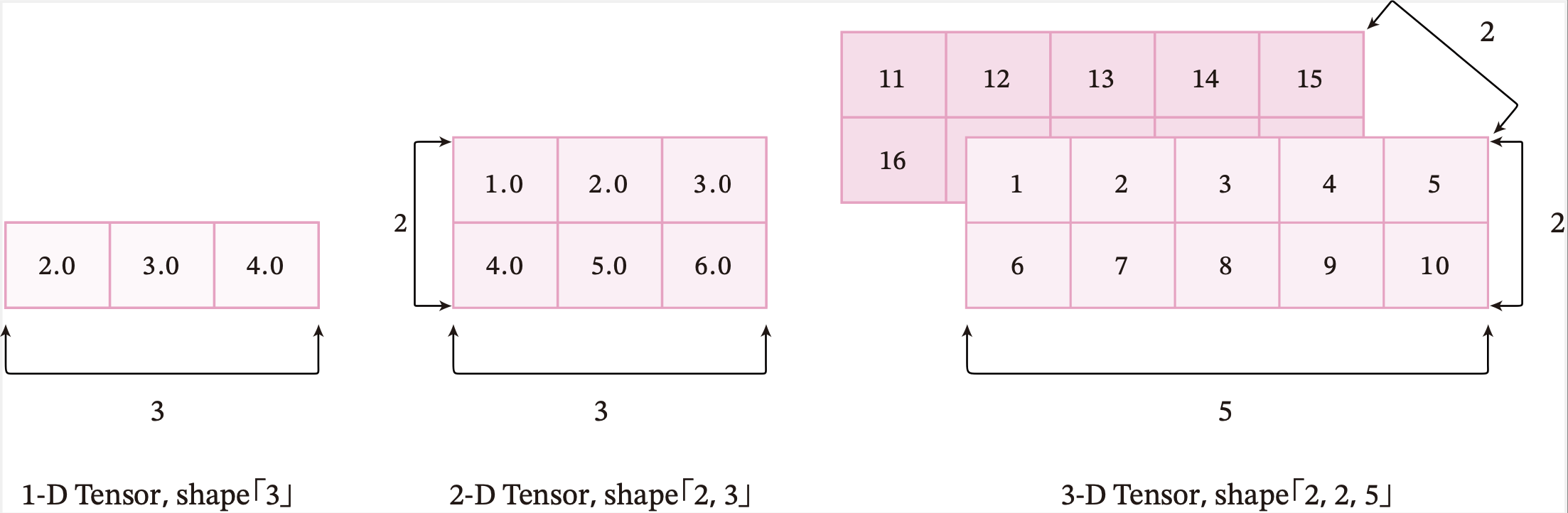
                                              图1.5 不同维度的张量可视化表示

 

张量中元素的类型可以是布尔型数据、整数、浮点数或者复数，但同一张量中所有元素的数据类型均相同。因此我们可以给张量定义一个数据类型(dtype)来表示其元素的类型。

1.2自己的理解 

       张量连续存储，计算能力更快更强，可以看成多维数组。支持cpu和gpu加速。高阶张量由多个低阶张量组成。Pytorch中的张量为torch.Tensor，即为torch下的Tensor类，其数据类型（dtype）有多种。

1.2. 使用pytorch实现张量运算

1.2.1 创建张量

1.2.1.1 指定数据创建

直接使用torch.Tensor（数据）创建

（1）一维：

import torch
first=torch.Tensor([2.0, 3.0, 4.0])
print(first)

结果：tensor([2., 3., 4.])

（2）二维：

first=torch.Tensor([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0]])
print(first)

结果：

        tensor([[1., 2., 3.],

                   [4., 5., 6.]])

（3）多维

first=torch.Tensor([[[1, 2, 3, 4, 5],
                 [6, 7, 8, 9, 10]],
                [[11, 12, 13, 14, 15],
                 [16, 17, 18, 19, 20]]])

结果：

         tensor([[[ 1.,  2.,  3.,  4.,  5.],

                    [ 6.,  7.,  8.,  9., 10.]],

                   [[11., 12., 13., 14., 15.],

                   [16., 17., 18., 19., 20.]]])

1.2.1.2 指定形状创建

torch.zeros(size) 是 PyTorch 中用来创建全 0 张量的函数。size 参数表示张量的形状（shape）.

torch.ones(size) 是 PyTorch 中用来创建全 1张量的函数。size 参数表示张量的形状（shape）.

torch.full(size, fill_value)返回创建size大小的形状，里面元素全部填充为fill_value的张量。

x=torch.zeros(2,3)
y=torch.ones(2,3)
print(x)
print(y)