数字信号处理：教程、概念与实践资源汇总-优快云博客

本文链接：https://blog.youkuaiyun.com/pzs0221/article/details/123019640

1. 视频教程

解放军信息工程大学-数字信号处理（国家级精品课）
空军工程大学-通信原理（国家级精品课）
西北大学 - 数据结构（国家级精品课）
csdn公式指导文档

手撕《现代信号处理》——通俗易懂的现代信号处理章节详解集合
 清泉_流响的博客
 数字信号处理专栏（坚持）
数字信号处理专栏（让学习成为一种习惯）
现代数字信号处理（第1学期）
现代数字信号处理（第2学期）
现代数字信号处理（第1学期2班）
现代数字信号处理（第1学期）
现代数字信号处理（第1学期清晰版）
无线通信系统C++实用模型：
https://github.com/zwm152/WirelessCommSystemSimuC-Model
https://github.com/LILYLINLIN/PracSim-WirelessCommSystemSimu
这个是fork上面的，但他的主页上还有：
https://github.com/LILYLINLIN/Information-theory-Communication_System_Simulation
有c++通信仿真：https://github.com/PiggyGaGa
https://github.com/mkmishra2000/Communication_System_in_CPP

2. 相关概念

2.1 数字频率

$x_a(t)=sin(2\pi f_0t) = sin(\Omega_0 t)$
$x(n)=x_a(nT)=sin(\Omega_0 nT)=sin(\omega n)$
$\omega = \Omega_0T = \Omega_0/F_s = 2\pi f$ 　为数字角频率，单位：弧度
$f=f_0/F_s$ 　　　　　　　　　为数字频率，无单位
$\omega = \Omega T$ 　　　　　　　　　　数字角频率＝模拟角频率ｘ采样周期
$N=\frac{2\pi }{ω_0}$ 　　　　　　　　　　周期
//-----------------------------------------------
$f_s$ 采样率
$N$ : FFT点数
则一次IQ字节数：

int 	fs = 12480;
int 	N = 4096;					//fft点数
double 	rs = fs/N;					//resolution频率分辨率
f=(0:N-1) * (fs/N)  				//频率范围；0 到 fs- fs/N
fn = (n-1)*fs/N						//n点的频率



//读取IQ
int len =  N*2*sizeof(short);		//如果IQ存储类型为short，或是float

3.开源库

Github上关于 “Digital Signal Processing language:C++” 的搜索

3.1 c++库

开源信号处理算法库介绍
 数字信号处理库（滤波）
数字信号处理c++类集合

Eigen官网

github:
https://github.com/vinniefalco/DSPFilters

3.2 FFTW

官网：http://www.fftw.org/index.html
全球最快的傅里叶变换算法（FFTW）
fftw的使用【本人博客】

tar -zxvf fftw-3.3.8.tar.gz
./configure --help
./configure CC=gcc -prefix=/home/xxx/fftwlib
make
make install

3.3、MKL

Intel的 MKL数学计算库，只支持 x86，源代码不开源，并优先支持 Intel 处理器，同时在 x86 生态，MKL 库的使用也最为广泛，原因主要是发展早，以及 intel 处理器在高性能计算领域的市场占有率极高有关。华为的KML 数学计算库支持华为鹏 ARM 处理器，不开源，按照“鹏应用使能套件 BoostKit 许可协议描述，仅面向签署该协议或者在鳃鹏硬件授权使用。
实战Intel MKL(Math Kernel Library)

3.4 intel IPP

Intel IPP库概述，合计共5000个函数

3.5 EIGN

EIGN用于矩阵计算
官网：https://eigen.tuxfamily.org/index.php?title=Main_Page

4、IQ数据分析

IQ数据简介
 详解IQ调制以及星座图原理
 用MATLAB读取MORSE、BPSK、QPSK信号的波形和频谱
 利用MatLAB绘制 QPSK 调制波形及其包络分析
根据保存的IQ信号，可以通过一系列数字信号处理技术解析出频谱视图。面是一种常见的方法：

IQ信号预处理：首先，对保存的IQ信号进行预处理，例如进行低通滤波以消除高频噪声。
采样率转换：根据需要得到的频谱视图的分辨率，可以进行IQ信号的采样率转换，使之适合频谱分析。
傅里叶变换：将IQ信号进行傅里叶变换，将时域信号转换为频域信号。傅里叶变换可以用快速傅里叶变换（FFT）算法来加快计算速度。
幅度谱计算：从傅里叶变换的结果中提取幅度信息，得到幅度谱。可以使用绝对值、平方等方法得到幅度谱。
频率轴转换：根据采样率和信号长度计算出频率轴的刻度，将幅度谱转换为频谱视图。
功率谱密度计算：根据幅度谱和信号长度计算功率谱密度（PSD），用于表示频谱视图中各频率分量的功率强度。
显示频谱视图：将计算得到的频谱视图以图形方式进行显示，可以使用散点图、折线图、瀑布图等形式展示频率和功率信息。

需要注意的是，解析出的频谱视图是对IQ信号进行频谱分析的结果，可以用于显示信号的频率成分和功率分布

1、SDR接收机下来的数据通常是IQ数据，合路成复数（a+bj）之后，做FFT一般得到的是单边带的频谱，在正半轴或者负半轴。
2、单独用其中一路，一样可以分析，做FFT得到的是双边带频谱
3、2M采样率的IQ数据为什么可以显示2M的带宽，而不是奈奎斯特采样率只能表示1M带宽。这个问题很容易理解了，直观的解释就是2M采样率得到的IQ数据做FFT得到的频谱不是对称的，并没有信息冗余。

I/Q两路采样可以降低采样率，可以获取信号的相位信息：

一是方便地将信号采用复信号的方法表示；
二是可以降低每个支路的采样率（因为如果用幅度检波后的采样率将是其两倍），降低对ADC的要求；
三是可以保留原始信号的相位信息。

5、频谱

频谱分析-FFT之后的那些事情
 FFT频谱分析（补零、频谱泄露、栅栏效应、加窗、细化、频谱混叠、插值），Matlab、C语言代码
 FFT之后为什么还要做fftshift？
MATLAB做FFT后为什么还要fftshift？
fftshift详解

fftshift 函数可以将 FFT 结果进行移动，使得频率为零的分量移动到中心位置。需要注意的是，在某些情况下，如果信号的长度不是偶数，则使用 fftshift 可能会导致频率分量的位置不正确，从而产生错误的结果。

Y = fftshift(X) 通过将零频分量移动到数组中心，重新排列傅里叶变换 X。
如果 X 是向量，则 fftshift 会将 X 的左右两半部分进行交换。
如果 X 是矩阵，则 fftshift 会将 X 的第一象限与第三象限交换，将第二象限与第四象限交换。
如果 X 是多维数组，则 fftshift 会沿每个维度交换 X 的半空间。
Y = fftshift(X,dim) 沿 X 的维度 dim 执行运算。例如，如果 X 是矩阵，其行表示多个一维变换，则 fftshift(X,2) 会将 X 的每一行的左右两半部分进行交换。

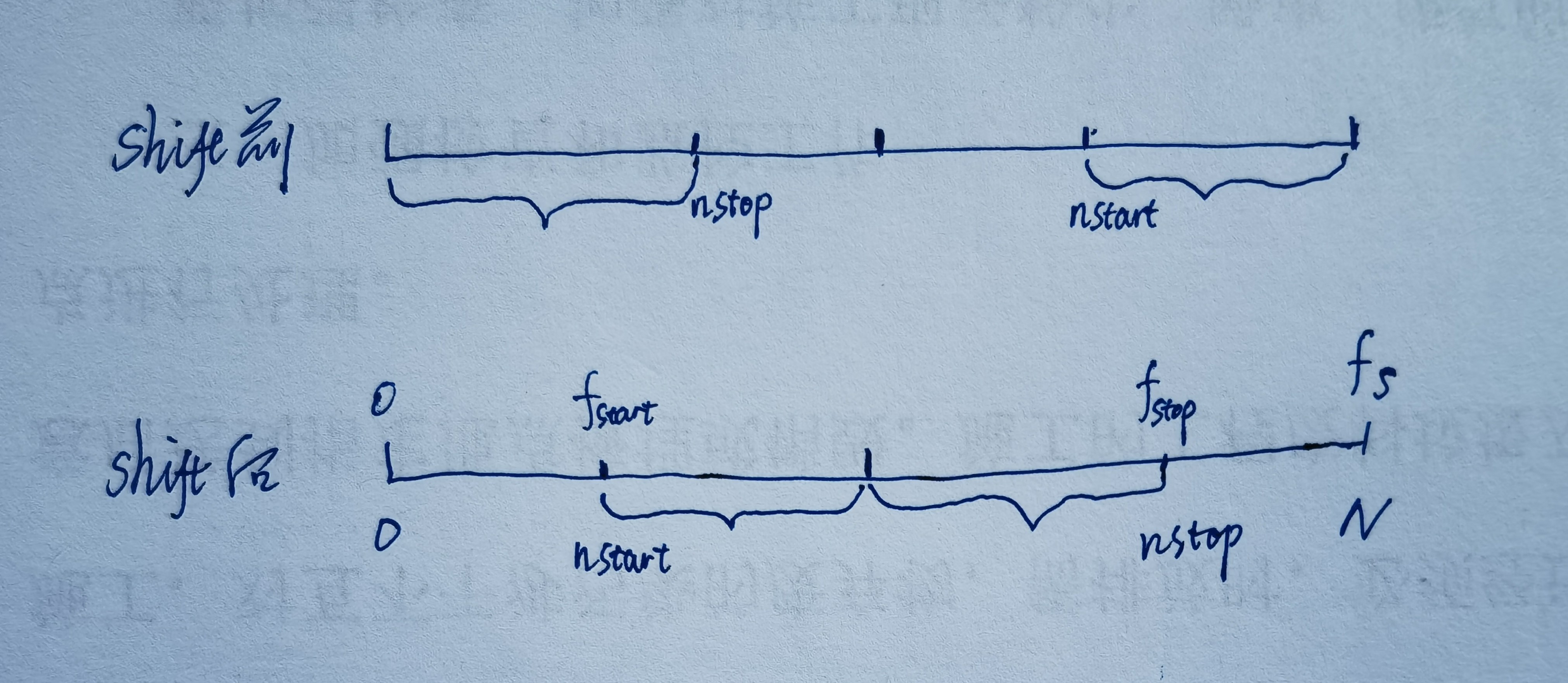
上图中的右侧最大频率应是：fs- fs/N

频段上有多少个谱线：

$n=\frac{f_{stop}-f_{start}}{f_s/N}+1=\frac{BN}{f_s}+1$

C语言总谐波失真（THD）实现，解决FFT频谱泄露和栅栏效应

5、信号产生

数字信号处理C++程序集
高斯白噪声：

#include <iostream>
#include <iterator>
#include <random>

int main() {
    // Example data
    std::vector<double> data = {1., 2., 3., 4., 5., 6.};

    // Define random generator with Gaussian distribution
    const double mean = 0.0;//均值
    const double stddev = 0.1;//标准差
    std::default_random_engine generator;
    std::normal_distribution<double> dist(mean, stddev);

    // Add Gaussian noise
    for (auto& x : data) {
        x = x + dist(generator);
    }

    // Output the result, for demonstration purposes
    std::copy(begin(data), end(data), std::ostream_iterator<double>(std::cout, " "));
    std::cout << "\n";

    return 0;
}

下面的高斯白噪声方法由Marsaglia和Bray在1964年提出,C++版本如下: mu是均值,sigma是方差,X服从N(0,1)分布：

double generateGaussianNoise(double mu, double sigma)
{
    static double V1, V2, S;
    static int phase = 0;
    double X;
    double U1,U2;
    if ( phase == 0 ) {
        do {
            U1 = (double)rand() / RAND_MAX;
            U2 = (double)rand() / RAND_MAX;

            V1 = 2 * U1 - 1;
            V2 = 2 * U2 - 1;
            S = V1 * V1 + V2 * V2;
        } while(S >= 1 || S == 0);

        X = V1 * sqrt(-2 * log(S) / S);
    } else{
        X = V2 * sqrt(-2 * log(S) / S);
    }
    phase = 1 - phase;
    return mu+sigma*X;
}

6、采样率转换

对信号做降采样处理时，需要先滤波，后抽取（降采样）；升采样操作与之相反

7、无线通信系统仿真

Simulating Wireless Communication systems - Practical Models in C++, [美], C. Britton Rorabaugh 著，王昕等译，电子工业出版社
IDE：Visual Studio 2022
问题描述：该书所附近代码，将main()函数前加上int后，在IDE中大多可以直接编译链接。早期的编译器在函数返回什缺失时隐含认为是int型，但在IDE中必须了显示地声明为int. 生成可执行代码后，运行时出现内存访问异常。
原因：各Model的Signal有Block_Size和Valid_Block_Size二个属性，但不知为什么后一个属性经常没有合理的设置。
解决方案：在各Signal的Initialize和Execute成员函数中，合理地设置Valid_Block_Size属性。

8、调制解调

8.1 各种调制方式介绍

1、SSB（Single Side Band）
单边带：非正弦信号
2、CW（Continuous Wave连续波）
CW通讯的优缺点

9、窗函数

在这里插入图片描述

9.1 汉明窗、汉宁窗

$\omega(n)=(1-\alpha)-\alpha cos(2\pi n/N)$ 0≤n≤N-1
$\omega(n)=0.54-0.46cos(2\pi n/N)$ $\alpha=0.46$ 汉明
$\omega(n)=0.5 - 0.5cos(2\pi n/N)$ $\alpha=0.5$ 汉宁

10、滤波

11、自适应滤波

自适应滤波器算法综述以及代码实现

12、DDC(Digital Down-Conversion)

数字下变频（DDC）基础知识
 MATLAB实现中频正交采样（数字下变频）

chatgpt生成的ddc代码（待验证）：

#include <iostream>
#include <complex>
#include <cmath>

// 定义FFT函数
void fft(std::complex<double>* x, int N) {
    if (N <= 1) return;

    std::complex<double> *even = new std::complex<double>[N / 2];
    std::complex<double> *odd = new std::complex<double>[N / 2];

    for (int i = 0; i < N / 2; i++) {
        even[i] = x[i * 2];
        odd[i] = x[i * 2 + 1];
    }

    fft(even, N / 2);
    fft(odd, N / 2);

    for (int k = 0; k < N / 2; k++) {
        std::complex<double> t = std::polar(1.0, -2 * M_PI * k / N) * odd[k];
        x[k] = even[k] + t;
        x[k + N / 2] = even[k] - t;
    }

    delete[] even;
    delete[] odd;
}

// 定义DDC函数
void ddc(std::complex<double>* signal, int N, double freq, double sampling_rate) {
    // 对信号进行FFT
    fft(signal, N);

    // 计算频率偏移
    double delta_f = freq / sampling_rate;

    // 对频谱进行频率偏移
    for (int i = 0; i < N; i++) {
        double phase_shift = -2 * M_PI * i * delta_f;
        std::complex<double> phase_factor = std::polar(1.0, phase_shift);
        signal[i] *= phase_factor;
    }
}

int main() {
    const int N = 8; // 信号长度
    const double sampling_rate = 100.0; // 采样率
    const double freq = 20.0; // 信号频率

    // 创建模拟信号
    std::complex<double> signal[N];
    for (int i = 0; i < N; i++) {
        double t = i / sampling_rate;
        signal[i] = std::complex<double>(std::cos(2 * M_PI * freq * t), 0);
    }

    // 执行DDC数字下变频
    ddc(signal, N, freq, sampling_rate);

    // 输出结果
    std::cout << "DDC后信号频谱：" << std::endl;
    for (int i = 0; i < N; i++) {
        std::cout << "信号频率 " << i * sampling_rate / N << " Hz: " << std::abs(signal[i]) << std::endl;
    }

    return 0;
}