男模Python-求解线性方程组

最新推荐文章于 2025-12-05 17:02:52 发布

原创最新推荐文章于 2025-12-05 17:02:52 发布 · 883 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#python #开发语言 #linux #学习 #程序人生 #php

python教学我们还继续吧

今天就练习求解线性方程组

你需要先执行

pip install sympy

注意是在python xxx.py的那个地方执行

pip install sympy

的意思是，从网络下载sympy软件包

sympy可以做一些带有符号的数学运算，比如带有未知数的线性方程组

记得弄一个新的文件

主要是理解pip是干什么的

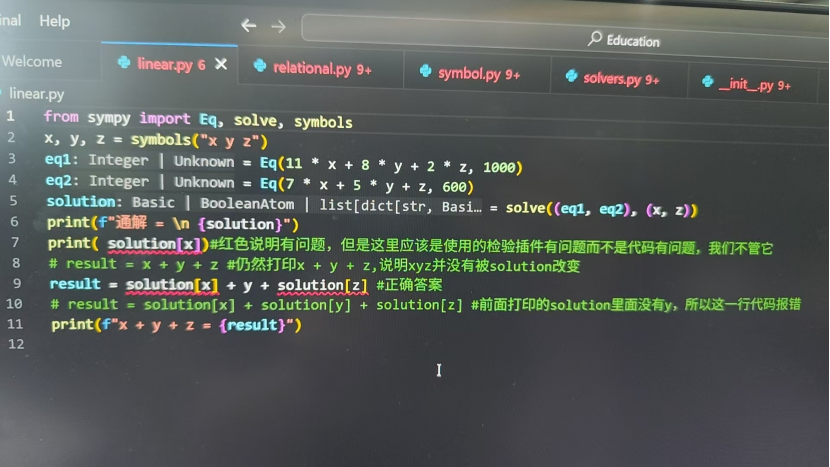
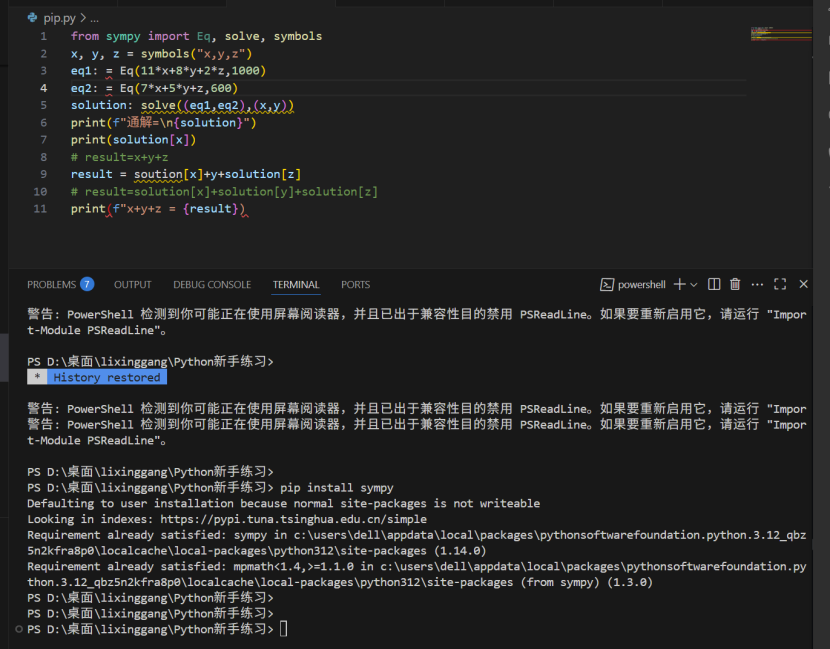
现在看看第二行

虽然它没有报错，但是新函数symbols你需要自己读文档看看他应该怎么用（文档是英文的，如果你不喜欢可以问deepseek，他应该也可以读这个文档的）

然后和我截图里面比较，你会发现正确写法是

x, y, z = symbols("x y z")

里面没有逗号

那么我是怎么知道这一点的呢？我也没有symbols的文档啊？

嗯原因很简单，因为我最初也是像你那样以为在参数字符串里面是用逗号分割的，但是这样程序执行不正确，检查了好几遍确定我这里没有问题之后，我就问了deepseek，怎么解线性方程组啊？它不仅告诉我怎么解，还会给我实例代码，实例代码中就有symbols函数的正确用法

x, y, z = symbols("x y z")我说的这句话代表什么意思？

在Python的符号计算库 SymPy 中，x, y, z = symbols("x y z") 是一条常用的语句，用于定义符号变量。它的作用如下：

1. 功能解释

symbols("x y z") 会创建三个符号变量 x, y, z（变量名与字符串中的名称一致）。

通过解包赋值（x, y, z = ...），这三个符号变量被分别绑定到变量名 x, y, z 上，方便后续使用。

2. 为什么需要这样做？

SymPy 要求在使用符号变量前显式声明它们。

例如，直接写 expr = x + y 会报错（除非 x 和 y 已定义为符号变量）。

3. 等价写法

也可以分开定义：

python

x = symbols('x')

y = symbols('y')

z = symbols('z')

但 symbols("x y z") 更简洁，且支持同时生成多个符号。

在Python的符号计算库 SymPy 中，x, y, z = symbols("x y z") 是一条常用的语句，用于定义符号变量。它的作用如下：

1. 功能解释

symbols("x y z") 会创建三个符号变量 x, y, z（变量名与字符串中的名称一致）。

通过解包赋值（x, y, z = ...），这三个符号变量被分别绑定到变量名 x, y, z 上，方便后续使用。

2. 为什么需要这样做？

SymPy 要求在使用符号变量前显式声明它们。

例如，直接写 expr = x + y 会报错（除非 x 和 y 已定义为符号变量）。

3. 等价写法

也可以分开定义：

python

x = symbols('x')

y = symbols('y')

z = symbols('z')

但 symbols("x y z") 更简洁，且支持同时生成多个符号。

是的，因为这里需要设置的是数学符号变量，它需要给接下来的Eq函数使用。

因为编程语言是不会自动支持数学符号变量的，只能通过这种方式告诉系统我们接下来要使用x, y, z 3个数学符号

在 SymPy 中，solve((eq1, eq2), (x, y)) 的作用是求解由 eq1 和 eq2 组成的方程组，并将 x 和 y 作为未知数解出。

1. 语法解析

python

solve((eq1, eq2), (x, y))

输入参数：

(eq1, eq2)：由 Eq 定义的方程组成的元组（表示方程组）。

(x, y)：指定要解的符号变量（未知数）。

输出：

返回一个字典 {x: sol_x, y: sol_y}，其中 sol_x 和 sol_y 是 x 和 y 的解（可能是表达式，也可能是数值）。

2. 具体示例

假设我们有以下方程组：

{11x+8y+2z=1000(eq1)3x+5y+7z=2000(eq2){11x+8y+2z=1000(eq1)3x+5y+7z=2000(eq2)运行以下代码：

python

from sympy import symbols, Eq, solve

# 定义符号变量

x, y, z = symbols("x y z")

# 定义方程

eq1 = Eq(11*x + 8*y + 2*z, 1000)

eq2 = Eq(3*x + 5*y + 7*z, 2000)

# 解方程组（x 和 y 用 z 表示）

solution = solve((eq1, eq2), (x, y))

print(solution)

输出可能类似：

python

{

x: (6100 - 46*z)/31,

y: (17000 - 71*z)/31

}

这表示：

x=6100−46z31,y=17000−71z31x=316100−46z,y=3117000−71z即解是用 z 表示的表达式（因为方程组有 3 个变量但只有 2 个方程，解不唯一）。

3. 关键点说明

解的情况：

如果方程数量等于未知数数量，通常能得到唯一解（数值或具体表达式）。

如果方程数量少于未知数数量（如本例），解会以剩余变量（如 z）的参数形式表示。

如果方程无解，返回空列表 []。

指定未知数的顺序：

solve((eq1, eq2), (x, y)) 和 solve((eq1, eq2), (y, x)) 的解顺序不同，但数学等价。

符号解与数值解：

SymPy 默认返回符号解（包含其他变量的表达式）。

如果需要数值解，可以代入具体值：

python

# 假设 z = 10，求 x 和 y 的数值解

solution_sub = {k: v.subs(z, 10) for k, v in solution.items()}

print(solution_sub) # 输出: {x: 180.0, y: 320.0}

4. 扩展用法

解更多方程：

如果有 3 个方程和 3 个变量，可以解出唯一解：

python

eq3 = Eq(x + y + z, 500)

solution = solve((eq1, eq2, eq3), (x, y, z))

解非线性方程：

solve() 也适用于非线性方程（如 x**2 + y = 5）。

5. 总结

solve((eq1, eq2), (x, y)) 是 SymPy 的核心功能之一，用于求解符号方程组。理解它的输入（方程和变量）和输出（解的字典形式）是使用 SymPy 进行符号计算的基础。

就是这样

只不过我们写的是

solve((eq1, eq2), (x, z))

而不是x, y

其实效果是一样的，

之所以是x, z，是因为我给李亚峰讲的时候就是这么写的，当时是手算的，x, z更简单一点，就先算x, z了