算法笔记
一、动态规划
典型题目:
打家劫舍
动态规划的核心思想是:将问题分解成子问题,f(0)、f(1)等子问题的最优解可以求出,那f2的问题就可以分解成f0和f1的子问题,当前状态有两种选择方式,列出两种方式,加上条件,一般从0、1、2最小子问题开始求,滚雪球逐渐向后推,和递推很像。
f(x) = max {f(x-1),f(x-1)+g(x)};
动态规划最重要两个点:1、当前状态和前一个状态的关系:通过0、1、2递推
·································2、初始值 边界值
滚动数组思想:
打家劫舍II:
用最少的空间,记录所有值。
1)将动态规划的轮次找出来
譬如:斐波那契数列:
f(0) = 1;
f(1) = 1;
f(2) = 2;
f(3) =3;
这个一维动态规划最少需要3个数,就可以求出后面所有的数列0、1、2。
所以用0、1、2重复记录后续数字:
f(3) = f(0)= f(1)+f(2)=3;
f(4)=f(1)=f(2)+f(3)=5;
f(5)=f(2)=f(3)+f(4)=8;
可以归纳f(x)=f(x%3) = f((x-1)%3) + f((x-2)%3);
2)二维动态规划:
打家劫舍II,
有障碍物的向右向下移动,可归纳的动态规划转移方程:

当该点有障碍物时,路线总数0;
当该点无障碍物时,路线总数=从左边到达+从上边到达的路线总数。

到达星的路线总数 = 两块框的路线总数之和。
也就是
如果利用滚动数组:
将 f(i,j) 看作当前轮次的 f(j), 将f(i-1,j) 看成上一轮次的 f(j),将 f(i)(j-1) 看成当前轮次的 f(j-1),
所以这就变成了只用一维数组来存储这个二维数组,只用一行来存储m行,每次到下一行,将上一行的一维数组替换掉
所以这就变成了:
f(j) = f(j) + f(j-1);
轰炸敌人:
四个方向的动态规划,将每个点的向上、向右、向左、向下四个方向上能够轰炸的敌人相加,分解为
当前点在向上方向能炸的敌人:
f(x,y) = f(x-1,y);//当前为空地
= 0;当前不为空地;
= f(x-1,y) +1;
单词拆分:
dp[i]表示前i个字符,是否能拆分成 列表内的单词。
边界dp[0]=空字符串=true;
方程:
dp[i] = dp[j] && check( str(i-j);
j为单词分割点,只需要判断后面的单词是否满足条件。
常用哈希表来快速判断字符串是否出现在字符串列表。
s.substr(j, i-j)来截取字符串。从j开始截取j-i个字符。
basic_string substr(size_type _Off = 0,size_type _Count = npos) const;
二、DFS-深度优先搜索:
遍历每个节点:且只走一遍
DFS是一种递归:从根节点-子节点-子节点-子节点 类似于树的先序遍历
深度优先搜索:
通常用递归实现。
void dfs(node) {
根。
左子节点。
右子节点。
}
1)树:
对树来说,深度优先搜索就像树的先序遍历,先遍历第一个节点,再向下遍历第一个节点的子节点,

按照FCADB的顺序遍历。
在写DFS时,记住先根遍历。
二叉树:
void dfs(node) {
printf(node->val);
dfs(node->left);
dfs(node->right);
}
图:
节点1:节点1的子节点并删除该节点的边
打家劫舍II(例)
dfs、动态规划、二叉树的后序遍历
树的结点为相邻点,树的节点有3种关系,父、左节点、右节点。
当前子节点被选中、不被选两种;
树的dfs实际是树的先序、中序、后续遍历。
2)图
数据结构:
unordered_map<string, priority_queue<string, vector, greater >> mp;
存储:点1:点2-点3-点4 (边)
点2:点1-点4-点5;
点3:…
伪代码:
void dfs(const string& str)
{
while (图中尚有点且点有边) {
获取该点;
删除该节点到下一个访问节点的边;即删除点1->点2,从点1种移除点2.
dfs(按顺序下一个相邻点); dfs(点2);
}
//无路可走,加入点:
res.emplace_back(str);
}
图示:
dfs()
{
访问点1;
删除点1的连接点点2,即删除1-2之间的边。
dfs(访问点2);
}
图的遍历:经过所有顶点,但走过的边不重复。
建图:
图的存储:邻接表、邻接矩阵。
1】邻接表:

1->(2、3、4);
2->(4);
3->(空);
4->(3);
这样存起来了图的顶点和边。
数据结构:map < int, vector>,int对应顶点,vector是边
图的DFS遍历:
从1开始,1->2,删除1-2之间的边,即变为1->(3、4),
dfs进入2:删除2-4之间的边,变为2->(空);
dfs进入4:删除4-3;
dfs进入3:空,结束;
至此,遍历顺序为1、2、4、3。
2]邻接矩阵:
vector<vector>>vec;
vec[0]顶点0对应的边,vec[0][1]顶点0-顶点1对应的边长度或有无。
3】有向图:
图中每个点都有个出入度。
无向图:每个点有几条边就有几个度。
一笔画问题:欧拉图
欧拉图:
通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路;半欧拉图能通不能回
通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路;**所有边一次,且能往回走,走回顶点。**欧拉图,能通能回起点。
重新安排行程:(例)
本题是让输出一条欧拉通路。
首先存储图,
判断是否有欧拉通路:
无向图:G连通且无奇数度顶点:边为奇数条。则有欧拉通路。
半欧拉图:G连通且有0、2个奇度顶点,只有两个边为奇数条。
**有向图:**只有一个强连通分量,且每个点的入边和出边数相同。
半欧拉图:
每个点的入边和出边数相同。
最多一个点,入边-出边=1;
最多一个点,出边-入边=1;
将有向图变无向图,它所有点是一个强连通分量。
遍历过程中的死胡同:
走到某个点时,该点已经不能向下走了,这点就是死胡同,也就是叶子节点,死胡同的点应最后遍历。
所以使用栈进行反转。
Hierholzer 算法:
1、从起点开始,向下深度优先遍历;
2、从某个顶点移动到另外一个顶点的时候,删除这条边。
3、无路可走,该点无出边,将该点加入到栈内。返回上一层
三、BFS_广度优先搜索
从图的某一点出发,依次遍历它的所有相邻节点,再从相邻节点出发,依次遍历它的相邻节点。
广度优先搜索通常用队列实现。
分为树和图。
1)树
队列qu:
根入队。
while(队列非空)
{
根出队
左孩子入队
右孩子入队
}
2)图:
图的算法先存储图节点和边。
边的存储:vector<vector> mp。
1:{2、3、4}
2:{1、4、5}
3:{1、4};
广度遍历:
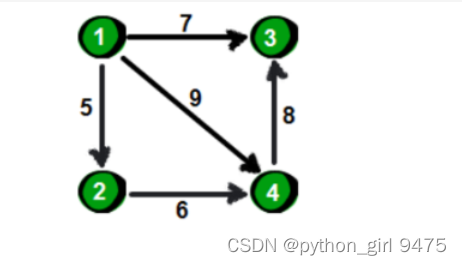
队列qu:
起点入队。
while(队列非空)
{
起始点出队;
该点的所有相邻点入队。2、3、4。
删除起始点和它们之间的边。//或者判断已加入过不需要再加
}
图比树多的一点就是需要判断曾经已经遍历过的,不需要再遍历。
1)被围绕的区域:
广度优先搜索,找到在边界上的O,找到和它相连的O,将其标记为A,然后遍历所有数组,被标记的不变,其余变为X
遇到这种围绕的区域,需要四个方向上查找的,可以将方向记为数组:
dx[4]={0,0,1,-1};
dy[4]={1,-1,0,1,0};
这样便将四个方向记录了下来;
遍历的时候只需要x+dx[i], y+d[y[i];来向四个方向行走;
四、二分查找
int BinarySearch(int arr[], int len, int target) {
int low = 0;
int high = len;
int mid = 0;
while (low <= high) {
mid = (low + high) / 2;
if (target < arr[mid]) high = mid - 1;
else if (target > arr[mid]) low = mid + 1;
else return mid;
}
return -1;
}
搜索二维矩阵
五、字符串
最长回文子串:
六、拓扑排序
拓扑排序是一种图论;
无环又向图
1)含义:

排序方式:
1)找到一个无入度的点:
1或者2
2)将其入栈并删除该点(或标记该点为已遍历),将该点的出边全部删除;
3)重复1)和2)
最后的排序顺序为:
1、2、3、4、5、6、7、9;
拓扑排序可能有多种情况,这只是其中的一种情况;
2)常用方法:
都要一个边集,访问数组,结果数组/栈
1】常和DFS一起:后序遍历。
*栈+DFS+一个数组(标记该点是否被访问过)。
vector<vector> edges;
vector visited;
stack result;
先将出度为0的入栈,删除该点和入度边。
具体方法:
挨个遍历图中的点。
每个点进行DFS遍历,每个点分3种情况:已遍历、遍历中、未遍历,常用visit[i]表示。
已遍历的加入栈。

我们将当前搜索的节点 u 标记为「搜索中」,遍历该节点的每一个相邻节点 v:

当 u 的所有相邻节点都为「已完成」时,我们将 u 放入栈中,并将其标记为「已完成」。
```cpp
for(int i = 0; i < numCourses; ++i) {
if (!visit[i]) {
dfs(i);
}
}
void dfs(int u) {
visited[u] = 1;//标记为遍历中
for (int v: edges[u]) {//遍历u的相邻点v
if (visited[v] == 0) {
dfs(v);
if (!valid) {
return;
}
}
else if (visited[v] == 1) {
valid = false;
return;
}
}
visited[u] = 2;//最后标记u为已访问
}
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/course-schedule/solution/ke-cheng-biao-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
图示:
```cpp
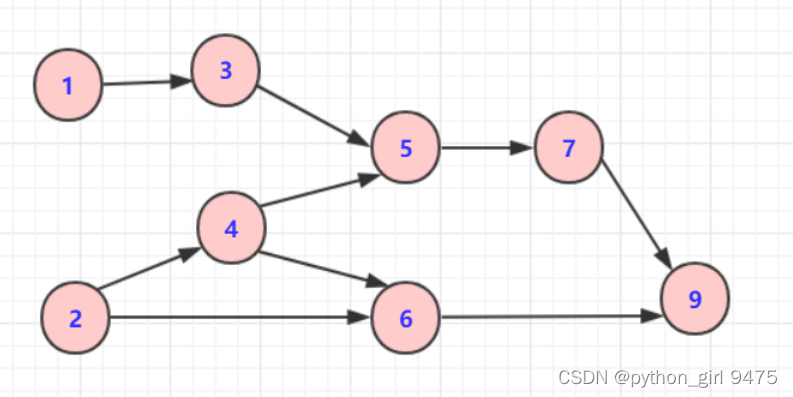
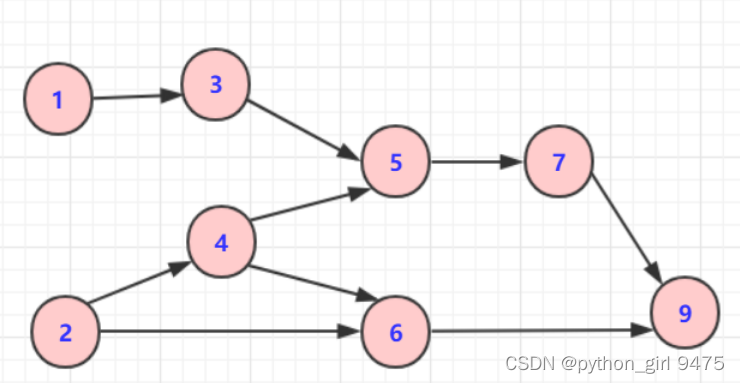
遍历:1
将1标记为访问中
遍历1的相邻点3
判断3是未访问,
遍历:3
判断3的相邻点5,将5标记为访问中
遍历:5
将7标记为访问中
遍历:9
将9标记为访问中;
9,无相邻点,入栈,标记为已访问。
退出。
9入栈,标记9为已访问。
...
...
2】BFS+队列
正向遍历,先将入度为0的入队列,再删除该点的出边。
vector<vector> edges;//维护边
vector indeg;//维护入度
queue q;
寻找入度为0的点,将所有入度0加入队列内。
for (int i = 0; i < numCourses; ++i) {
if (indeg[i] == 0) {
q.push(i);
}
}
//初始加入入度0的点。
int visited = 0;
while (!q.empty()) {
++visited;
int u = q.front();
q.pop();
for (int v: edges[u]) {
--indeg[v];
if (indeg[v] == 0) {
q.push(v);
}
}
}
//当访问过的节点和节点数量相同时,它可以为拓扑排序。
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/course-schedule/solution/ke-cheng-biao-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
课程表
存储:
有向图用:vector<vector>存储,每个点对应各自的出边;
七、差分
差分数组对应的概念是前缀和数组。
含义:
对于数组[1,2,2,4],其差分数组为[1,1,0,2],
原数组->差分数组:[1-0,2-1,2-2,4-2],得到差分数组:d[i] = a[i]-a[i-1];
差分数组->原数组:[1,1+1,1+1+0,…],得到原数组:a[i] = d[i] + d[i-1];
原数组是差分数组的前缀和数组;
差分数组:
差分数组的性质是,当我们希望对原数组的某一个区间[l,r] 施加一个增量inc 时,差分数组d对应的改变是
d[l] = d[l] + inc;
d[r] = d[r+1] - inc;
表示在l这个点上增加了inc,从r+1开始减少inc;
这样可以O(1)的完成对差分数组的修改,并且修改可以叠加
最后将差分数组求前缀和得到原数组即可;
航班预订系统
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
vector<int> nums(n);
for (auto& booking : bookings) {
nums[booking[0] - 1] += booking[2];
if (booking[1] < n) {
nums[booking[1]] -= booking[2];
}
}
for (int i = 1; i < n; i++) {
nums[i] += nums[i - 1];
}
return nums;
}
};
获得区间;
维护差分数组;
恢复原数组;
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/corporate-flight-bookings/solution/hang-ban-yu-ding-tong-ji-by-leetcode-sol-5pv8/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
滑动窗口
滑动窗口i,j;
定义两个指针 start 和 end 分别表示子数组(滑动窗口窗口)的开始位置和结束位置,维护变量 sum 存储子数组中的元素和(即从
nums[start] 到 nums[end] 的元素和)。
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/minimum-size-subarray-sum/solution/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
初始状态下,end 都指向下标 0,sum 的值为 0。

并查集:
并和查,连通性。
查:查当前节点的根节点
并:将两个根并在一起
只要根相同,就是一个队伍的,就是连通的
pre[] 存储上级节点
//查找根
int find (int root)
{
return root;
}
//合并两个集合
void join(int root1, int root2)
{
int x,y;
x = find(root1);//root1的根
y = find(root2);//root2的根
if (x!=y)
{
pre[x] = y;
}
路径压缩
冗余连接:
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
int[] parent = new int[n + 1];
for (int i = 1; i <= n; i++) {
parent[i] = i;
}
for (int i = 0; i < n; i++) {
int[] edge = edges[i];
int node1 = edge[0], node2 = edge[1];
if (find(parent, node1) != find(parent, node2)) {
union(parent, node1, node2);
} else {
return edge;
}
}
return new int[0];
}
public void union(int[] parent, int index1, int index2) {
parent[find(parent, index1)] = find(parent, index2);
}
public int find(int[] parent, int index) {
if (parent[index] != index) {
parent[index] = find(parent, parent[index]);
}
return parent[index];
}
}
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/redundant-connection/solution/rong-yu-lian-jie-by-leetcode-solution-pks2/
来源:力扣(LeetCode)
单调栈
用来解决,一维数组,找前后的距离最近的比该数大的数 或比该数小的数。
单调栈可以单调增可以单调减。
例:
每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
这是一个单调递减的栈,要找每个数从后边往前,第一个比当前数小的数:
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
vector<int> ans(n);
stack<int> s;
for (int i = 0; i < n; ++i) {
while (!s.empty() && temperatures[i] > temperatures[s.top()]) {
int previousIndex = s.top();
ans[previousIndex] = i - previousIndex;
s.pop();
}
s.push(i);
}
return ans;
}
};
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/daily-temperatures/solution/mei-ri-wen-du-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
柱状图中的最大矩形
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








