python_深度学习 数据处理

监督式学习任务：分类和回归

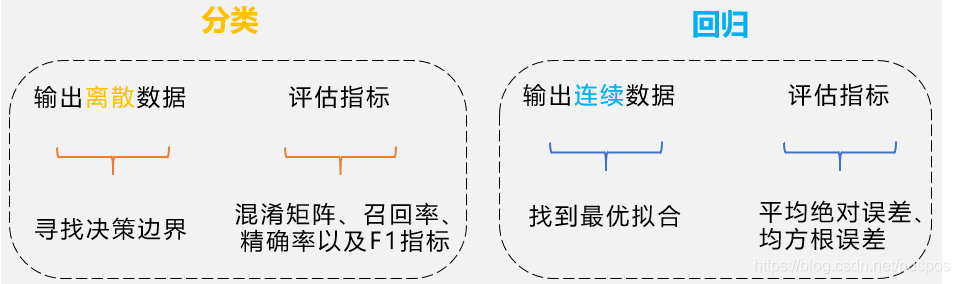
分类

预测每个类别的概率，概率最大的即是

预处理+特征

1.数据向量化

神经网络所有的输入和label目标都是浮点数张量（特定下，是整数张量）

• 文本向量化
  • 文本分割为字符（中文一个字，英文一个字母），将每个字符转换为一个向量
  • 文本分割为单词（中文一个词，英文一个单词），将每个单词转换为一个向量
  • 提取单词或字符的n-gram，将每个n-gram转换为一个向量。

2.值标准化

归一化：手写数字分类

标准化：

3.处理缺失值

空值：pandas中是""
缺失值：df中是NAN(数字，eg:年龄），NaT（日期类型datetime，eg:生日 1995-2-1），None(字符串，eg:性别）

3.1判断缺失值

df.isnull()返回true／false的DataFrame
df.isnull().any()返回Series,显示哪些列有缺失值(该列名下，其值为true)
df.isnull().sum()返回Series，显示每个列各有多少缺失值
df.info()看每个列有多少个非缺失值

3.2处理缺失值

• 对缺失值较多的特征，删掉该特征（列）

#删除含有缺失值的行或列
df.dropna()#删除包含缺失值的特征
DataFrame.dropna(axis=0,how='any',thresh=None,subset=None,inplace=Flase)
'''
axis=0:对列操作，将该特征舍弃，=1时，舍弃缺失值所在的行
how:默认'any'，只有一行/列存在缺失值，就将该行/列丢弃，'all'时，一行/列所有的值都是缺失值时才丢弃
thresh：int型，eg:thresh=3，该行/列至少出现了3个才将其丢弃
inplace:默认False，True时为直接对数据进行修改
'''

• 若样本缺失值适中

该特征为离散类型，可以将缺失值作为一个新类别
该特征为连续类型，可以将其离散后，把离散值作为一个新类别

• 缺失值较少的特征（10%以内）

  • 填充

df.fillna(method='ffill')==df.ffill()
df.fillna(method='bfill')==df.bfill()
   DataFrame.fillna(value=None, method=None, axis=None, inplace=False, limit=None, downcast=None, **kwargs)
'''
value:用什么值填充，常量，字典/Series(按列填充)
axis:确定行还是列，与method配套出现
method: 不可与value同时出现
	'ffill'，axis=0时为用该缺失值所在列上面的值填充该缺失值
			 axis=1时为用该缺失值所在行前面的值填充该缺失值
	'bfill'，axis=0时为用该缺失值所在列下面的值填充该缺失值
	         axis=1时为用该缺失值所在行后面的值填充该缺失值

inplace=True时：直接在原数据上进行修改

'''

* 固定值填充，0填充，只要0不是一个有意义的值

df.fillna(0)

* 均值填充（中位数，众数，最大值，最小值）

#将所有的缺失值按所在列的均值进行填充,value可为常数，字典，Series，但只能按列填充
df=df.fillna(df.mean())==df.fillna(df.mean(axis=0))

* 上下数据填充

#用该列中缺失值上面的那个值来填充该缺失值
df.fillna(axis=0,method='ffill')
#用该行中缺失值前面的那个值来填充该缺失值
df.fillna(axis=1,method='ffill')
#用该列中缺失值前面的那个值来填充该缺失值
df.fillna(axis=0,method='bfill')
#用该行中缺失值上面的那个值来填充该缺失值
df.fillnae(axis=1,method='bfill')

* 算法拟合填充(==优先使用==)

#定义price缺失值预测填充函数
from sklearn.ensemble import RandomForestRegressor
def set_missing(df):
	#把已有的数值型特征取出来
	temp_df = df[['price','列名1','列名2',..]]
    #将数据分为该特征缺失和该特征存在的两部分
    know=temp_df[temp_df.price.notnull()].values
    unkown=temp_df[temp_df.price.isnull()].values
    
    #X为特征属性值
    X=know[:,1:]
    #以price列为y
    y=know[:,0]
    
    #
  rfr=RandomForestRegression(random_state=0,n_estimators=2000,n_jobs=-1)
    rfr.fit(X,y)
    
    #用得到的预测结果填补原缺失值
    predicted=rfr.predict(unknow[:,1:])
    
    df.loc[(df.price.isnull()),'price']=predicted
    return df,rfr

new_df,rfr=set_missing(df)

• 替换

• 若train中有缺失值，test中无缺失值，可用条件均值/条件中值替换成该缺失值

条件均值：该label下的缺失值所属特征的均值

• 若train和test中均有大量缺失值时，可以将该特征是否有缺失值作为一种特征

对于该特征，缺失值变为0，非缺失值为1

4.特征工程

选择什么特征给模型学习

batch_size,epoch,iter

每batch_size个样本后，进行一次梯度下降，为义词iterations（迭代）

• 遍历全部数据算一次损失函数，批梯度下降（batch gradient decent）计算开销大，计算速度慢，不支持在在线学习
• 一个数据算一次损失函数，随机梯度下降（stochastic gradient descent），速度快，收敛性能不太好，不收敛，在最优点晃来晃去，无法到达优点
• mini_batch即batch_size，一般为2的幂(8~128)，便于GPU上的内存分配

epochs为训练多少个完整样本，多少轮
$$oneepoch=iterations\times batch\_size$$
在LSTM中我们还会遇到一个seq_length,其实
batch_size = num_steps * seq_length

欠拟合和过拟合

欠拟合和过拟合的表现

• 欠拟合：训练集上准确率不高，测试集上准确率也不高【语料偏少，特征偏多】
• 过拟合：训练集上准确率特别高，在测试集上的准确率不高

防止过拟合

• 最优：数据集扩增：让训练集中的噪音数据比重占比少

• 次优：对模型允许存储的信息加以约束，如果一个网络只能记住几个模式，就只让其集中学习最重要的模式，降低模型复杂度

  • 减少网络容量：减小参数个数（【容量】eg:层数，隐藏单元数），来降低模型复杂度

  • 权重正则化(weight regularization)，通过强制让模型权重取较小的值（让模型权重变小）来降低模型复杂度，奥卡姆剃刀（如无需要，勿增实体，若有两个解释，选择最简单，假设更少的那个）

    • 范数，$x是一个向量，它的Lp范数$:
      $$\Vert x{\Vert }_p={\left(\sum _i{\left|x_i\right|}^p\right)}^{\frac{1}{p}}$$

    • 正则化方法 目标函数后加一个系数的惩罚项
      $$\begin{gathered} \overline{J}(w,b)=J(w,b)+\frac{\lambda }{2m}\Omega (w) \\ \frac{\lambda }{2m}是常数，m为样本数，\lambda 是超参数，用于控制正则化程度 \end{gathered}$$

      • L1正则化时，让原目标函数加上了所有特征系数绝对值的和，对应惩罚项为：
        $$\Omega (w)=\Vert w{\Vert }_1=\sum _i\left|w_i\right|$$

      • L2正则化时，让原目标函数加上了所有特征系数的平方和，对应惩罚项为：
        $$\Omega (w)=\Vert w{\Vert }_2^2=$$