目录
数据可视化技术——相关类图表总结
一、实验概述
(一)实验目的
深入理解散点图、气泡图、相关图、热力图、二维密度图及散点图矩阵的特点与应用场景,掌握使用Python工具(Matplotlib、Seaborn库)实现各类图表的流程,并通过实际案例分析数据相关性。
(二)实验环境
- 硬件环境:个人计算机(CPU: Intel Core i5,内存: 16GB)
- 软件环境:Windows 10系统,Python 3.9,库依赖:Matplotlib 3.7.1、Seaborn 0.12.2、Pandas 2.0.3、Numpy 1.26.0。
二、相关类可视化图表实现与分析
(一)散点图(Scatter Plot)
1. 特点
通过平面直角坐标系中散点的分布展示两个变量的线性或非线性关系,适用于初步探索变量间的关联趋势,可通过回归线增强趋势分析。
2. 应用场景
分析身高与体重、学习时间与成绩等两两变量的相关性。
3. 实现代码
import matplotlib.pyplot as plt
import numpy as np
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False
# 生成数据:身高与体重的模拟关系
np.random.seed(42)
height = np.random.normal(170, 10, 100)
weight = 0.7 * height - 50 + np.random.normal(0, 10, 100)
# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(height, weight, alpha=0.7, color='steelblue', edgecolors='w', s=80)
# 添加回归线
z = np.polyfit(height, weight, 1)
p = np.poly1d(z)
plt.plot(height, p(height), "r--", linewidth=2)
plt.text(150, 90, f'回归线: y = {z[0]:.2f}x + {z[1]:.2f}', color='red')
plt.title('身高与体重的关系')
plt.xlabel('身高 (厘米)')
plt.ylabel('体重 (公斤)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
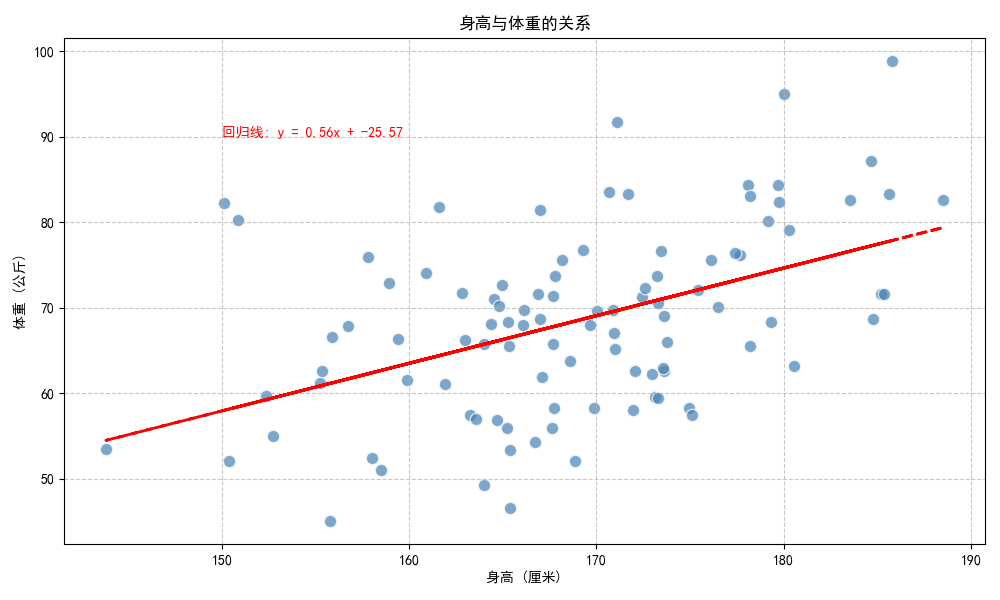
4. 结果分析
散点呈现从左下到右上的趋势,回归线斜率为正(约0.7),表明身高与体重呈正相关,符合生理规律。
(二)气泡图(Bubble Plot)
1. 特点
在散点图基础上引入第三个变量(气泡大小),可同时展示三个变量的关系,颜色映射可进一步扩展信息维度。
2. 应用场景
分析城市发展指标(如人均GDP、绿化覆盖率、人口)、市场分析中的销量-价格-利润关系等。
3. 实现代码
import matplotlib.pyplot as plt
import numpy as np
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False
# 示例数据:中国主要城市发展指标
cities = ['北京', '上海', '广州', '深圳', '杭州', '南京', '成都', '武汉', '重庆', '西安']
gdp_per_capita = [16.4, 15.7, 13.1, 15.8, 14.8, 14.1, 9.4, 13.5, 7.5, 9.3]
population = [2154, 2424, 1490, 1303, 980, 843, 1633, 1108, 3102, 1000]
green_area_ratio = [43.5, 38.2, 41.5, 45.0, 40.3, 42.5, 38.0, 39.5, 36.5, 35.0]
# 气泡大小映射人口数据
bubble_size = np.array(population) # 直接使用原始数据,缩放因子为1
# 绘制气泡图
plt.figure(figsize=(12, 8))
scatter = plt.scatter(gdp_per_capita, green_area_ratio, s=bubble_size, alpha=0.6,
c=population, cmap='viridis', edgecolors='w', linewidth=1.5)
# 添加城市标签
for i, city in enumerate(cities):
plt.annotate(city, (gdp_per_capita[i], green_area_ratio[i]), xytext=(5, 5),
textcoords='offset points', fontsize=10)
plt.title('中国主要城市人均GDP与绿化覆盖率关系')
plt.xlabel('人均GDP (万元)')
plt.ylabel('绿化覆盖率 (%)')
plt.colorbar(scatter, label='城市人口 (万人)')
# 添加气泡大小图例
for size in [500, 1000, 2000]:
plt.scatter([], [], s=size, alpha=0.6, color='gray', label=f'{size}万人')
plt.legend(scatterpoints=1, frameon=False, title='城市人口')
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
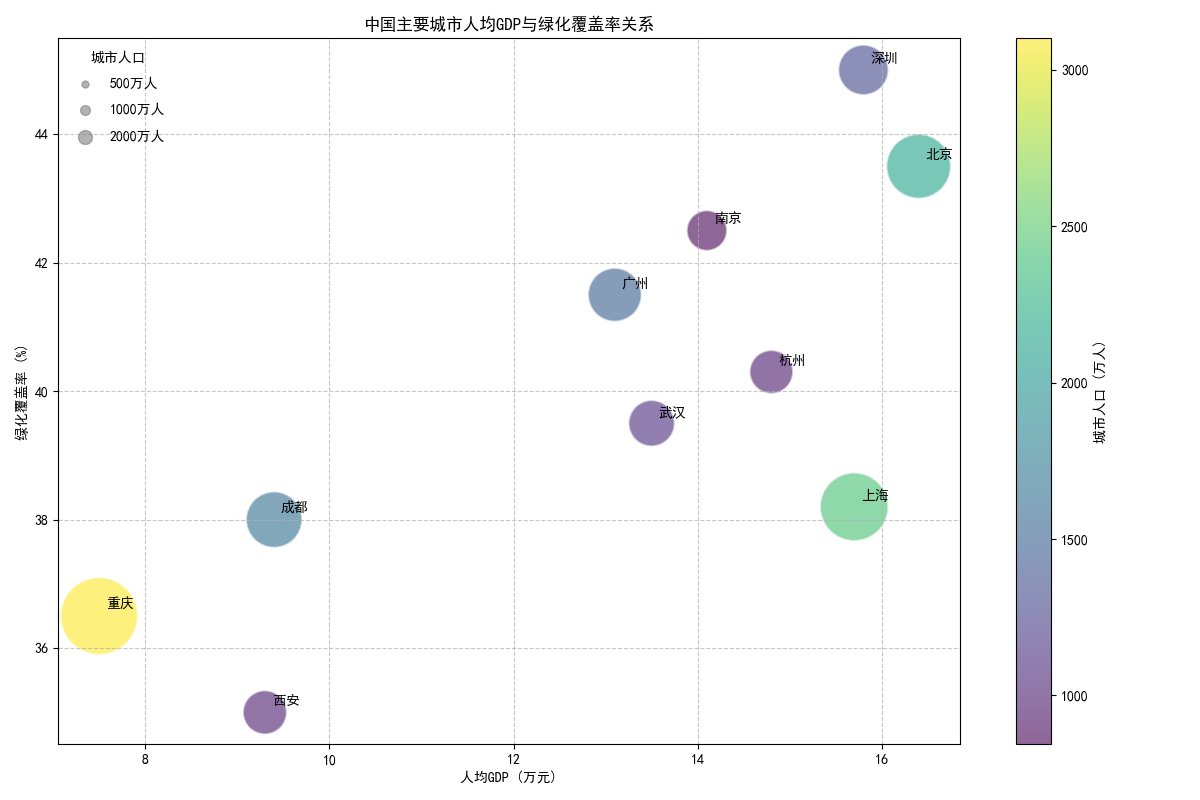
4. 结果分析
深圳、北京等城市人均GDP较高且绿化覆盖率较好,重庆人口最多但人均GDP较低,气泡大小与颜色清晰反映了人口与经济、环境指标的关联。
(三)相关图(Correlation Plot,热力图形式)
1. 特点
通过计算变量间的相关系数矩阵,以热力图颜色深浅展示相关程度(红色为正相关,蓝色为负相关),适用于多变量整体关联分析。
2. 应用场景
分析学生各科成绩相关性、金融指标联动性、生物特征关联性等。
3. 实现代码
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False
# 生成学生成绩数据(含相关性)
np.random.seed(42)
n_students = 100
corr_matrix = np.array([[1.0, 0.7, 0.3, 0.2, 0.1],
[0.7, 1.0, 0.4, 0.3, 0.2],
[0.3, 0.4, 1.0, 0.6, 0.5],
[0.2, 0.3, 0.6, 1.0, 0.7],
[0.1, 0.2, 0.5, 0.7, 1.0]])
means = [75, 80, 65, 70, 85]
cov = np.diag([10, 12, 15, 10, 8]) @ corr_matrix @ np.diag([10, 12, 15, 10, 8])
scores = np.random.multivariate_normal(means, cov, n_students)
df = pd.DataFrame(scores, columns=['数学', '语文', '英语', '物理', '化学'])
# 绘制相关图
plt.figure(figsize=(10, 8))
sns.heatmap(df.corr(), annot=True, cmap='coolwarm', square=True,
linewidths=0.5, annot_kws={'size': 10})
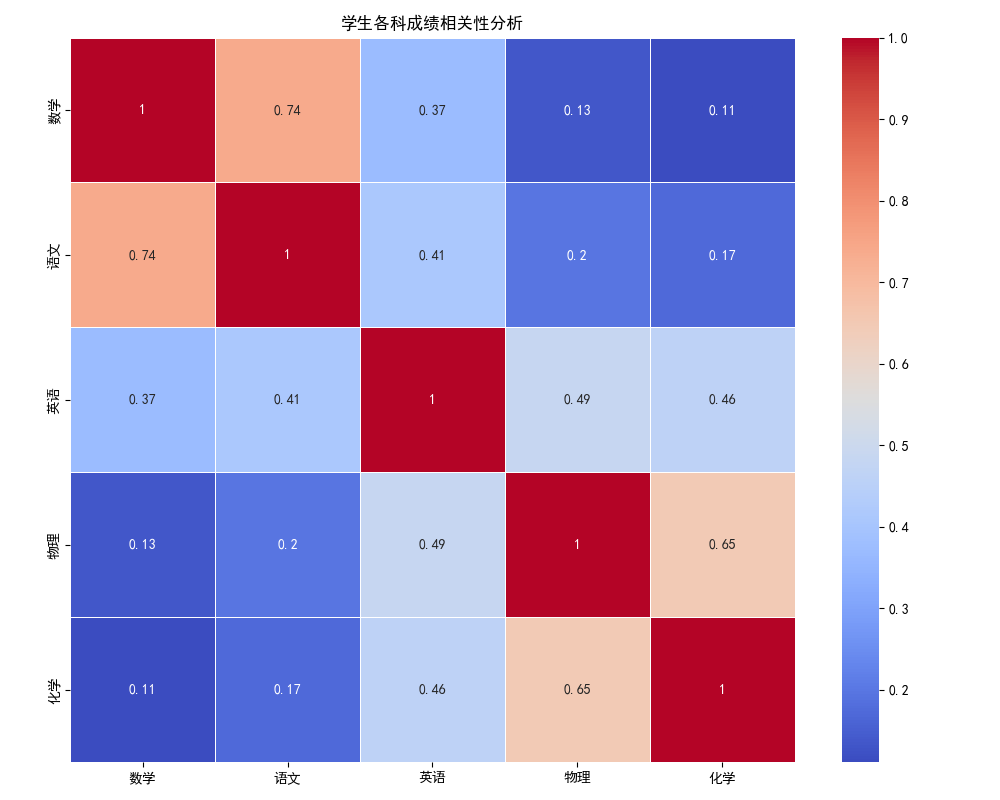
plt.title('学生各科成绩相关性分析')
plt.tight_layout()
plt.show()
4. 结果分析
数学与语文(0.7)、物理与化学(0.7)呈强正相关,英语与化学(0.5)呈中等相关,直观展示了科目间的关联强度。
(四)热力图(Heatmap,通用矩阵数据)
1. 特点
以颜色编码展示矩阵数据的分布,适用于呈现数据密度、频次或数值差异,支持行列聚类(本例未展示聚类)。
2. 应用场景
月度销售数据、用户行为频次、地理区域指标分布等。
3. 实现代码
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False
# 生成电子产品月度销售数据
np.random.seed(42)
months = ['一月', '二月', '三月', '四月', '五月', '六月',
'七月', '八月', '九月', '十月', '十一月', '十二月']
products = ['手机', '笔记本电脑', '平板电脑', '智能手表', '耳机']
data = np.random.randint(1000, 50000, size=(5, 12))
data[:, 6:] = data[:, 6:] * 1.5 # 下半年销量增长50%
data = data.astype(int)
df = pd.DataFrame(data, index=products, columns=months)
# 绘制热力图
plt.figure(figsize=(12, 8))
sns.heatmap(df, annot=True, fmt="d", cmap="YlGnBu",
linewidths=.5, cbar_kws={"label": "销售额(元)"})
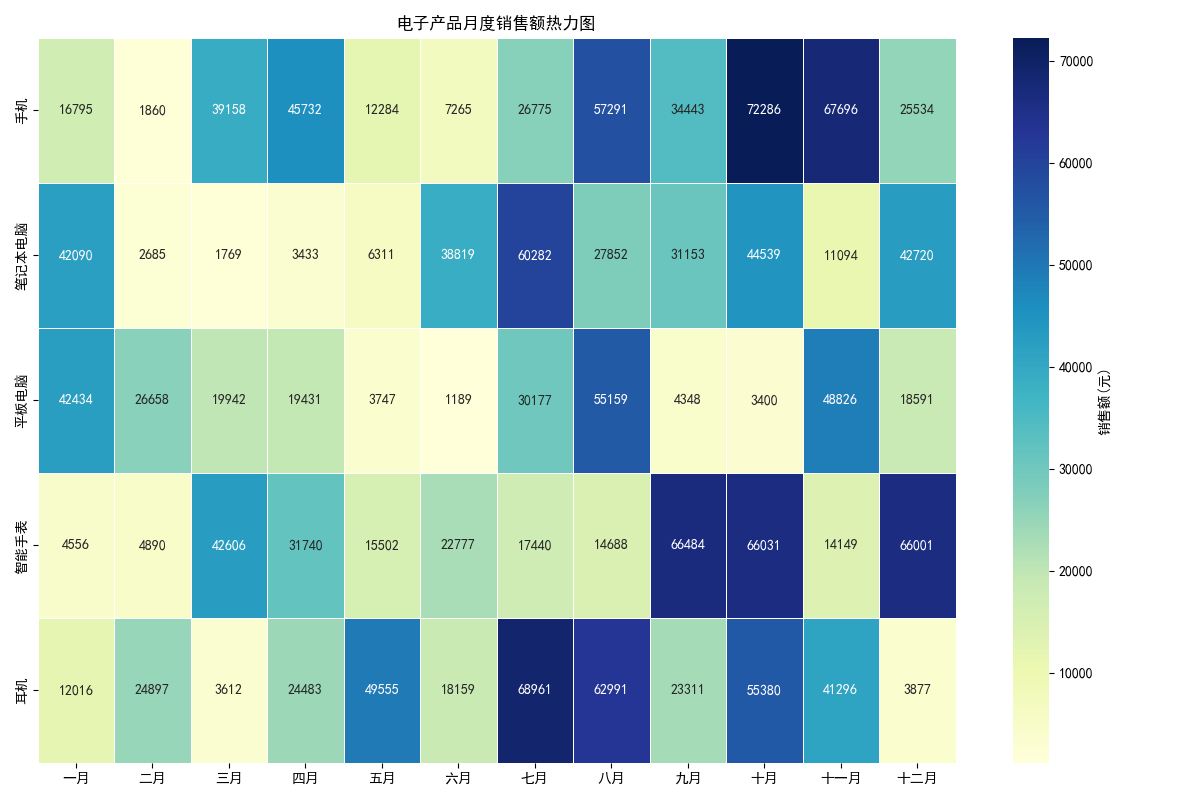
plt.title('电子产品月度销售额热力图')
plt.tight_layout()
plt.show()
4. 结果分析
下半年(七月至十二月)销售额普遍高于上半年,手机和笔记本电脑在十二月销售额最高(颜色最深),反映季节性消费趋势。
(五)二维密度图(2D Density Plot)
1. 特点
结合散点图与核密度估计,用颜色填充展示两个连续变量的联合分布密度,适用于数据量大、重叠多的场景。
2. 应用场景
分析房价与面积、年龄与收入、温度与湿度的分布关系。
3. 实现代码
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
# 设置中文字体,优先使用幼圆
plt.rcParams["font.family"] = ["YouYuan", "SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False
# 生成房价与面积数据
np.random.seed(42)
n_samples = 500
area = np.random.gamma(8, 10, n_samples)
area = np.clip(area, 30, 200)
price = 2 * area + 50 + np.random.choice([0, 50, 100, 150], size=n_samples, p=[0.3, 0.4, 0.2, 0.1]) + np.random.normal(0, 30, n_samples)
price = np.clip(price, 100, 800)
df = pd.DataFrame({'面积(㎡)': area, '价格(万元)': price})
# 绘制二维密度图
plt.figure(figsize=(12, 8))
sns.kdeplot(x='面积(㎡)', y='价格(万元)', data=df, cmap='Blues', fill=True, bw_adjust=0.8, thresh=0.05)
plt.scatter(area, price, alpha=0.3, color='gray', s=20, label='数据点')
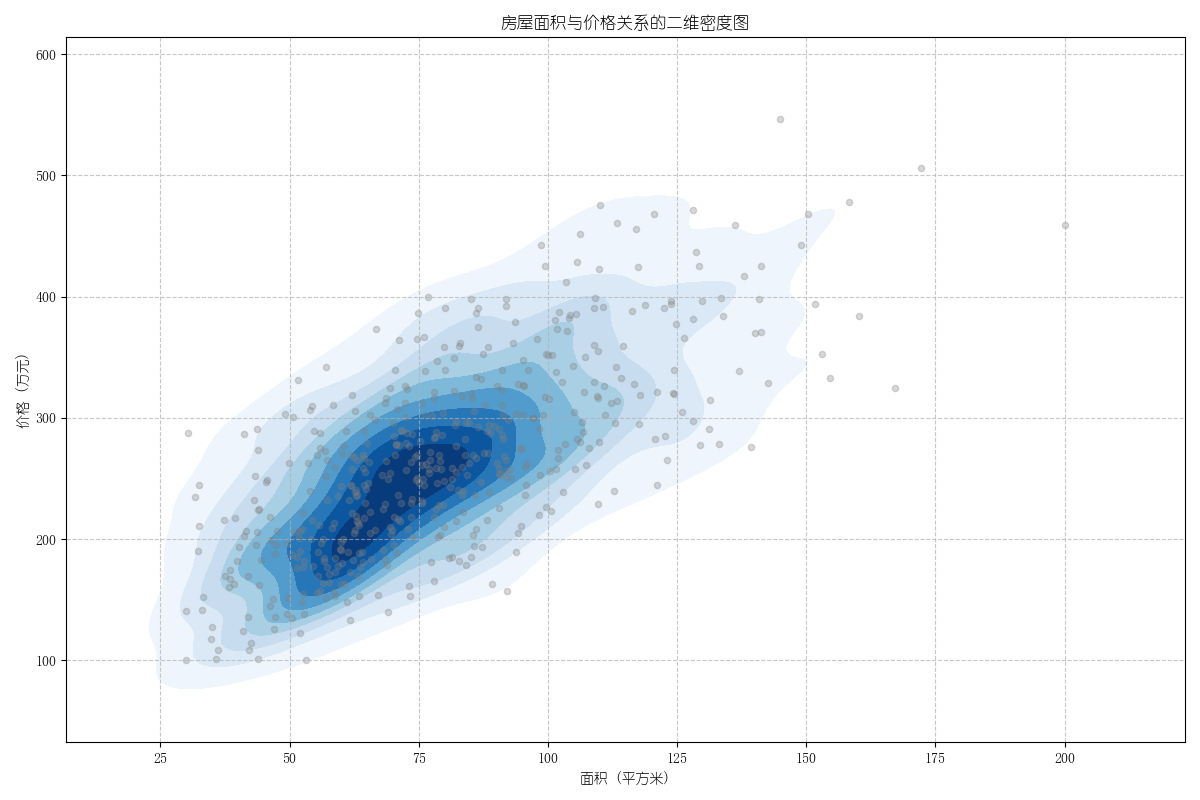
plt.title('房屋面积与价格关系的二维密度图')
plt.xlabel('面积 (平方米)')
plt.ylabel('价格 (万元)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
4. 结果分析
颜色越深区域表示数据越密集,图中显示面积在80-120平方米、价格在200-400万元区间为高密度区域,反映主流房价与面积的分布。
(六)散点图矩阵(Scatter Plot Matrix)
1. 特点
将多个变量两两组合为散点图,对角线展示单变量分布(核密度图或直方图),一站式呈现多变量间的全部关联。
2. 应用场景
多变量探索性分析(如学生成绩与学习习惯、金融多指标联动)。
3. 实现代码
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False
# 生成学生成绩与学习习惯数据
np.random.seed(42)
n_students = 100
data = {
'数学成绩': np.random.normal(75, 15, n_students),
'语文成绩': np.random.normal(80, 12, n_students),
'英语成绩': np.random.normal(78, 10, n_students),
'每天学习时间(小时)': np.random.normal(4, 1.5, n_students),
'每周阅读量(小时)': np.random.normal(6, 2, n_students)
}
# 添加相关性:成绩与学习时间/阅读量正相关
data['数学成绩'] += 0.6 * (data['每天学习时间(小时)'] - 4) * 10
data['语文成绩'] += 0.5 * (data['每周阅读量(小时)'] - 6) * 8
data = {k: np.clip(v, 0, 100) if '成绩' in k else np.clip(v, 0, None) for k, v in data.items()}
df = pd.DataFrame(data)
# 绘制散点图矩阵
plt.figure(figsize=(14, 12))
g = sns.pairplot(df, diag_kind='kde', markers='o', height=2.5,
plot_kws=dict(s=30, edgecolor="w", linewidth=1, alpha=0.7),
diag_kws=dict(shade=True))
plt.suptitle('学生成绩与学习习惯的散点图矩阵', fontsize=18, y=1.02)
plt.tight_layout()
plt.show()
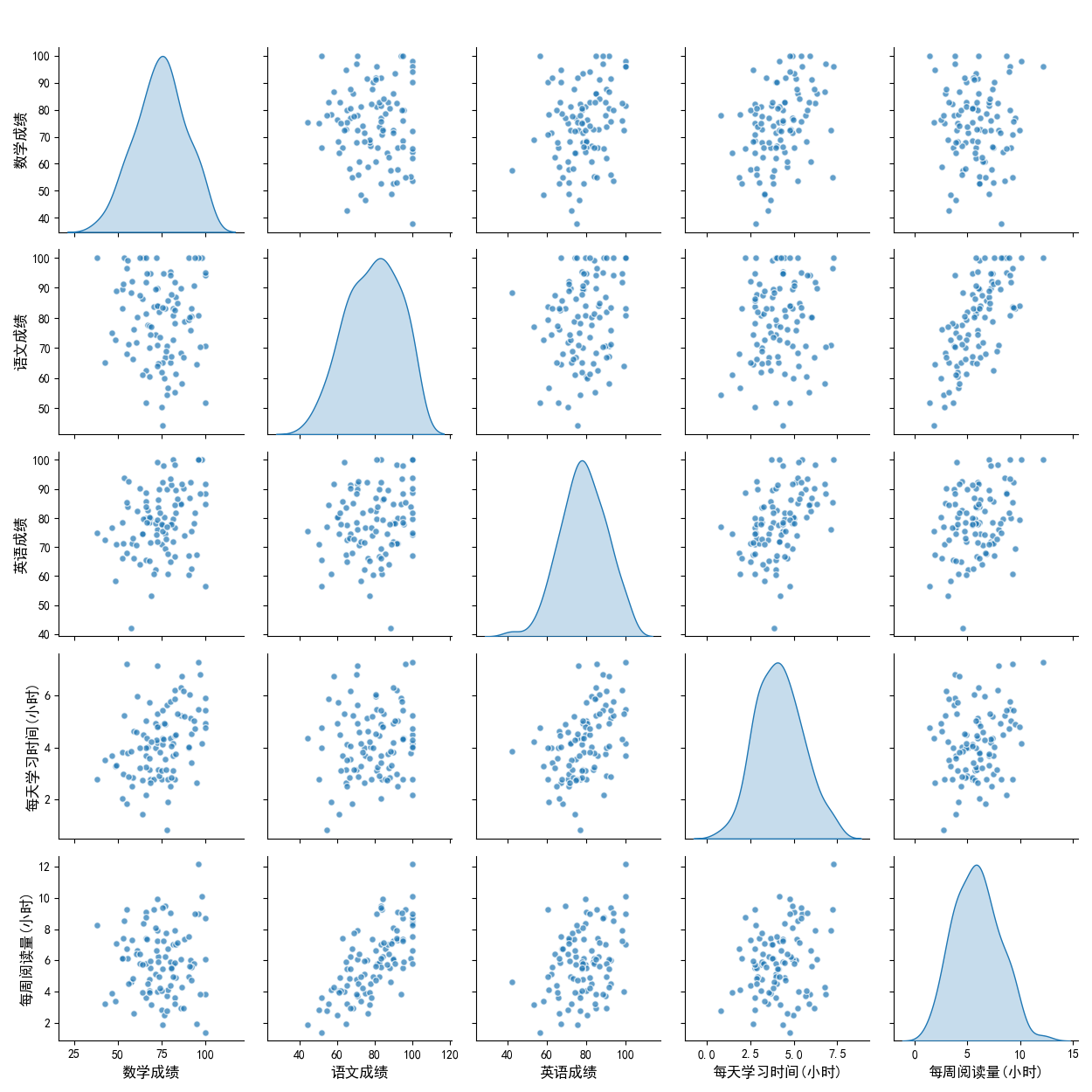
4. 结果分析
数学成绩与每天学习时间的散点图呈明显正相关,语文成绩与每周阅读量的散点图也有正趋势,对角线核密度图显示成绩分布集中在70-90分,学习时间集中在3-5小时/天。
三、六种图表总结对比
| 图表类型 | 核心特点 | 典型应用场景 | 关键工具/函数 | 数据维度 | 优势 |
|---|---|---|---|---|---|
| 散点图 | 两变量散点分布,展示线性/非线性关系 | 身高与体重、学习时间与成绩 | matplotlib.scatter | 2维 | 直观呈现变量间基础关联,支持回归线添加 |
| 气泡图 | 散点图+气泡大小(第三变量),颜色可映射第四变量 | 城市经济指标(人均GDP、绿化覆盖率、人口) | matplotlib.scatter | 3-4维 | 多维度信息集成,适合对比分析 |
| 相关图(热力图) | 相关系数矩阵热力图,颜色表示相关程度与正负性 | 多变量整体关联分析(如科目成绩相关性) | seaborn.heatmap | ≥2维 | 快速定位强相关/负相关变量对,适合多变量初探 |
| 热力图 | 矩阵数据颜色编码,展示数值分布或密度 | 月度销售数据、用户行为频次 | seaborn.heatmap | 2维 | 突出数据差异,适合展示结构化矩阵数据 |
| 二维密度图 | 核密度估计+颜色填充,展示两变量联合分布密度 | 房价与面积、年龄与收入 | seaborn.kdeplot | 2维 | 处理大数据量重叠问题,清晰呈现分布形态 |
| 散点图矩阵 | 多变量两两散点图+对角线单变量分布,一站式展示全部关联 | 学生成绩与学习习惯、金融多指标分析 | seaborn.pairplot | ≥3维 | 全面系统,适合探索性数据分析,快速发现变量间复杂关系 |
四、实验总结
通过本次实验,深入掌握了六种相关类可视化图表的原理、应用场景及Python实现方法,核心收获如下:
(一)图表选择逻辑
- 两变量分析:优先使用散点图(基础关联)或二维密度图(分布密度)。例如,分析身高与体重的线性关系时,散点图直观展示趋势;而分析房价与面积的分布时,二维密度图更适合处理500条数据的密集场景。
- 三/四变量分析:气泡图通过大小和颜色扩展维度,适合展示城市发展的多维指标(人均GDP、绿化覆盖率、人口)。
- 多变量整体分析:相关图(热力图形式)和散点图矩阵是核心工具。前者聚焦相关系数,后者兼顾两两关联与单变量分布,适用于学生成绩、金融指标等多变量探索。
(二)工具使用技巧
- Matplotlib与Seaborn的互补性:
- Matplotlib提供底层绘图控制(如气泡图标签标注、散点样式调整);
- Seaborn封装高级功能(如
pairplot一键生成散点图矩阵、kdeplot自动计算密度分布),大幅提升多变量图表开发效率。
- 中文字体与负号显示:通过
plt.rcParams全局设置字体(如幼圆、黑体)和负号渲染,避免图表出现乱码。
(三)数据解读关键
- 趋势与异常值:散点图和二维密度图中,趋势线(如回归线)和高密度区域可揭示变量间规律,远离集群的散点需进一步分析(如气泡图中的重庆人口异常值)。
- 相关系数的业务含义:相关图中数学与语文成绩的高相关(0.7)可能反映学生综合学习能力,而物理与化学的强相关(0.7)则与学科关联性一致。
- 季节性与分布特征:热力图通过颜色块分布清晰展示电子产品下半年销量增长,二维密度图则凸显房价与面积的“正态核”分布特征。
(四)局限性与扩展方向
- 图表复杂度:散点图矩阵在变量数>5时会显得拥挤,可结合主成分分析(PCA)降维后再可视化;
- 动态交互:可扩展至Plotly等库实现交互式图表(如悬浮提示、动态筛选),提升数据探索灵活性;
- 领域特定场景:在地理信息分析中,可结合二维密度图与地图工具(如Basemap),展示空间数据分布。
五、关键实验代码附录
| 图表类型 | 关键参数 | 作用 |
|---|---|---|
| 散点图 | alpha=0.7、edgecolors='w' | 控制透明度与边框,提升数据点辨识度 |
| 气泡图 | s=bubble_size、c=population | 气泡大小映射第三变量,颜色映射第四变量 |
| 相关图 | annot=True、cmap='coolwarm' | 显示相关系数值,冷暖色调区分正负相关性 |
| 热力图 | fmt="d"、cbar_kws={"label": "销售额(元)"} | 数值格式化为整数,添加颜色条标签 |
| 二维密度图 | fill=True、bw_adjust=0.8 | 启用颜色填充,调整核密度带宽平滑度 |
| 散点图矩阵 | diag_kind='kde'、height=2.5 | 对角线使用核密度图,控制子图尺寸 |
通过本次实验,我不仅熟练运用Python实现各类相关图表,更深刻理解了“数据可视化是探索数据的眼睛”——合理选择图表类型可显著提升数据分析的效率与深度。未来可结合具体业务场景,进一步优化图表交互性与解读维度。




















 2073
2073

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








