随机过程基础3--宽平稳随机过程的谱分析

本节关于随机过程的谱分析,当然是针对宽平稳随机过程
1,什么是谱?
将复杂对象分解成几个方面,使得我们可以从几个方面尽可能简单地观察这个复杂对象的某些特征.
例如光谱是按照光的波长分解.

对于随机信号来说,和确定性信号一样,是按照频率进行分解的.

我们先来回顾一下,确定性信号的频谱分析.

首先我们从确定性周期信号开始研究.首先了解了傅里叶级数,展开式如上,其中wr表示的就是所说的基频,=2pi/T,并且其中参数ak的表达式如上.
从ak表达式我们可以看出,傅里叶级数干的事情其实就是将-T/2到T/2的区间展开成各级数相加.用来近似函数,级数越多,近似越精确.

那么对于非周期函数,我们同样能进行傅里叶级数展开,不过只是在-T/2到T/2的区间上展开,在其他地方,进行的是周期延拓.

这里有一个注意点,

我们选择的展开基在-无穷到无穷上是正交的.

根据这个函数的正交性,我们得以推导出ak的公式.也就证明了傅里叶变换的展开基是正交的


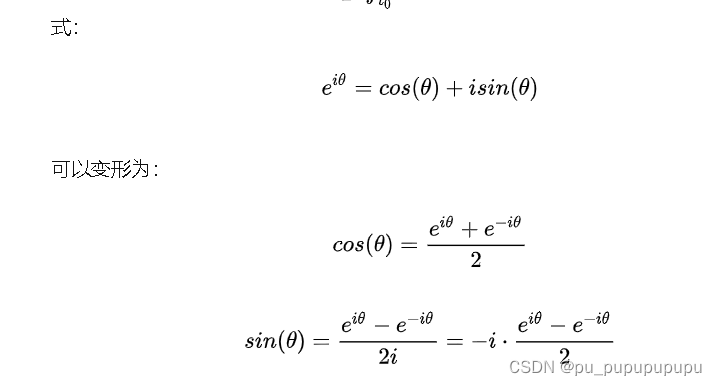
以上是从三角级数到指数级数的转化.这样我们根据正交性可以求出每一个ak.(由于正交所以,左右两边同时乘以基函数,就得到了ak)

第二步,将傅里叶级数扩展,使之不止在一个周期内展开

这里的思想就是T趋于无穷,但是当我们把傅里叶级数写出来的时候,马上发现2pi/T是趋于0的.观察上面的式子,可以看到这个2pi/T趋近于0但是以k倍慢慢相加,知道k趋于无穷,很容易让我们想到积分.

那么一个级数如何写出积分呢?式子如上.我们发现将2kpi/T当成xk,我们缺一个xk的无穷小变化量.精妙之处在于,我们给他补上这个变化量.2pi/T

因为本来就有一个1/T,所以只需要在前面加一个1/2pi.