n 皇后问题

放弃吧，不会有人给我点小心心的

【搜索/回溯】n 皇后问题

描述

在一个n×n国际象棋盘上，有n个皇后，每个皇后占一格；要求皇后间不会出现相互“攻击”的现象，即不能有两个皇后处在同一行、同一列或同一对角线上。问共有多少种不同的方法。

 比如一个6*6的棋盘，就可以这样放

说明：

本题的解空间有两种做法：

1、用二维数组存放。

这种方法虽然直观好理解，但是程序实现稍微麻烦一点。比如a[i][j]，0表示不放，1表示放皇后

用二维数组a[i][j]=1，皇后的放置位置信息有两个：对应的行信息i ，对应的列信息 j

所以我们可以考虑用一维数组来存放

2、用一维数组: a[i]=j 表示i单元存放 j 对应二维数组的含义就是i行的皇后放置在j列

压缩为一维后，一个问题是：怎么判断当前要放的皇后位置跟前面已经放的皇后是在对角线上？

这个可以利用对角线的数学性质，对角线要么是45度，要么是135度，tan(45°)=1 ,tan(135°)=-1 。它们的绝对值都是1

假设前面的皇后位置是i和a[i]，当前皇后要放的位置是pos 和x，把它们看作两个坐标点，根据tan(45 or 135)=|pos-i|/|x-a[i]|=1

如果 |x-a[i]|==|pos-i|成立，那么当前的皇后就不能放在x上了

输入

n

输出

每行按字典序输出一种方案，每种方案按行顺序输出皇后所在的列号数，每个数字场宽为5。

输入样例 1 

4

输出样例 1

2 4 1 3
3 1 4 2

提示

来源

linziyu

------------------------------------------------------我是分割线------------------------------------------------------------

我们废话不多说，直接开始将思路

首先，提示里告诉我们，有两种方式来存皇后的位置，第一种是直接用二维数组，但实现有些麻烦（麻烦在哪？我也不知道），第二种是用一维数组a，不仅会节省空间，而且实现也容易

a[i]=j 表示i单元存放 j 对应二维数组的含义就是i行的皇后放置在j列

也就是说，数组a的下标 i 表示的是行，a[i]里面的数字表示的是皇后所在的列

------------------------------------------------------我是分割线------------------------------------------------------------

解决了存放的问题，我们就要想一想，怎么知道两个皇后会不会互相攻击呢？

首先我们知道，皇后在同一行、同一列、同一对角线上会互相攻击，判断是不是在同一行，我们只需要判断 i 是否相等，判断是不是在同一列，我们只需要判断a[i]是否相等，那怎么判断是否在同一对角线呢？

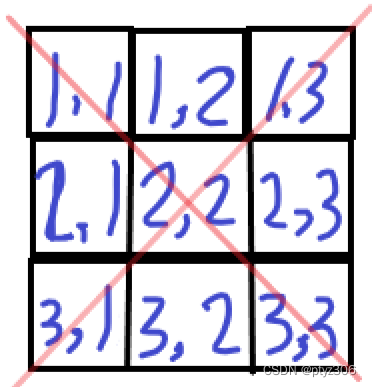
我们观察一下这个3*3的方格，他们的对角线上的坐标有什么共同点？

仔细观察一下

仔细观察一下

仔细观察一下

诶，我们发现，在同一对角线上的两个坐标（1,1）（2,2），在这两个坐标中，我们可以发现一个等式：

行减去行的绝对值=列减去列的绝对值

我们来验证一下这个规律：

坐标（1,3）（3,1），行减去行的绝对值=2，列减去列的绝对值=2, 2=2，所以（1,3）（3,1）在一条对角线上

坐标（2，2）（3,3），行减去行的绝对值=1，列减去列的绝对值=1, 1=1，所以（2,2）（3,3）在一条对角线上

所以，我们就可以用一个函数来判断两个坐标是否会攻击：

bool gj(long long x,long long y){//判断是否会攻击
	for(int i=1;i<x;i++){
		if(y==a[i])return 0;
		if(x+y==i+a[i])return 0;
		if(x-y==i-a[i])return 0;
	}
	return 1;
}

其中，x和y表示的是某一个点的坐标，把这个坐标拿去比对，判断会不会和其他皇后相互攻击

大概就是这个意思

------------------------------------------------------我是分割线------------------------------------------------------------

接下来，我们就可以正常地写出一个dfs

然后，我们就可以把这道题目做出来啦！！！！！

完整代码：

#include<bits/stdc++.h>
using namespace std;
long long n,a[105];
bool gj(long long x,long long y){//用于判断某个点会不会和其他皇后相互攻击，会返回0，不会返回1 
	for(int i=1;i<x;i++){
		if(y==a[i])return 0;
		if(x+y==i+a[i])return 0;
		if(x-y==i-a[i])return 0;
	}
	return 1;
}
void f(long long k){//总共有n行棋盘，k表示当前搜索到了第几行 
	if(k>n){//如果k>n，说明已经找到了一种方案 
		for(int i=1;i<=n;i++){
			cout<<setw(5)<<a[i];//输出这个方案 
		}
		cout<<endl;//换行 
	}
	for(int i=1;i<=n;i++){
		if(gj(k,i)){//判断把皇后放在（k，i）可不可以 
			a[k]=i;//可以就放上去 
			f(k+1);//往下一层搜索 
			a[k]=0;//搜索完后，回来擦除标记（a数组既有存储位置的作用，又有标记的作用） 
		}
	}
}
int main(){
	cin>>n;//读入n 
	f(1);//从第一行开始寻找答案 
	return 0;
}

------------------------------------------------------我是分割线------------------------------------------------------------

于是，这篇文章就这么愉快地结束了，这道也这么愉快地讲完了

还有一件事，我做过的大部分n皇后问题，n的范围都很小，都是6到13，但把我搜索的代码放上去就超时了，所以，你可以仔细地看一看n的范围，考虑考虑你要不要打表