图的m着色问题与图的最大团问题关系及利用该关系改进最大团问题的上界-优快云博客

本文链接：https://blog.youkuaiyun.com/psvm_123/article/details/143083521

1. m-着色问题（Graph m-Coloring Problem）

m-着色问题是将图的顶点分配给 m 种颜色，使得相邻顶点具有不同的颜色。对于一个图 G=(V,E)，需要找到一个函数 f:V→{1,2,...,m}，使得对于每一条边 (u,v)∈E，有 f(u)≠f(v)。图的染色数 χ(G) 是能实现合法着色所需的最小颜色数。

2. 最大团问题（Maximum Clique Problem）

最大团问题是寻找图中的最大团（Clique）。团是图的一个完全子图，即其中任意两个顶点都有边相连。最大团的大小 ω(G) 是图中包含的最大完全子图的顶点数。找到一个团意味着找到一个子集 C⊆VC，使得子图 G[C]是一个完全图，并且 |C| 尽可能大。

3.关系

图的染色数 χ(G)是最大团大小 ω(G)的上界之一。最大团的大小不会超过图的染色数，即：

ω(G)≤χ(G)

通过求解图的 m-着色问题来改进最大团问题的上界。

以下代码通过图的着色算法计算染色数 χ(G)，并利用该染色数作为最大团的一个上界。

import networkx as nx
from itertools import combinations
import matplotlib.pyplot as plt

# 创建一个图
G = nx.Graph()

# 添加图中的边
edges = [(0, 1), (0, 2), (1, 2), (1, 3), (2, 3), (3, 4), (4, 5), (4, 6), (5, 6)]
G.add_edges_from(edges)

# 判断子集是否为团的函数
def is_clique(G, nodes):
    """检查一个给定的顶点子集是否为团"""
    subgraph = G.subgraph(nodes)
    return len(subgraph.edges()) == len(nodes) * (len(nodes) - 1) // 2

# 查找图中的最大团
def find_max_clique(G):
    """查找图中的最大团"""
    n = len(G.nodes())
    max_clique = []
    
    # 从较大的顶点子集开始查找最大团
    for r in range(n, 0, -1):
        # 生成所有r个顶点的组合
        for nodes in combinations(G.nodes(), r):
            if is_clique(G, nodes):
                max_clique = nodes
                return max_clique  # 一旦找到最大团，直接返回
    return max_clique

# 使用networkx的greedy_color函数实现图的贪心着色
colors = nx.coloring.greedy_color(G, strategy="largest_first")
chromatic_number = max(colors.values()) + 1  # 染色数是最大颜色数 + 1

# 查找图中的最大团
max_clique = find_max_clique(G)
clique_size = len(max_clique)

# 输出结果
print(f"图的染色数 (χ(G)): {chromatic_number}")
print(f"最大团的大小 (ω(G)): {clique_size}")
print(f"利用染色数改进的最大团上界: {chromatic_number}")

# 绘制图，并标注最大团的顶点
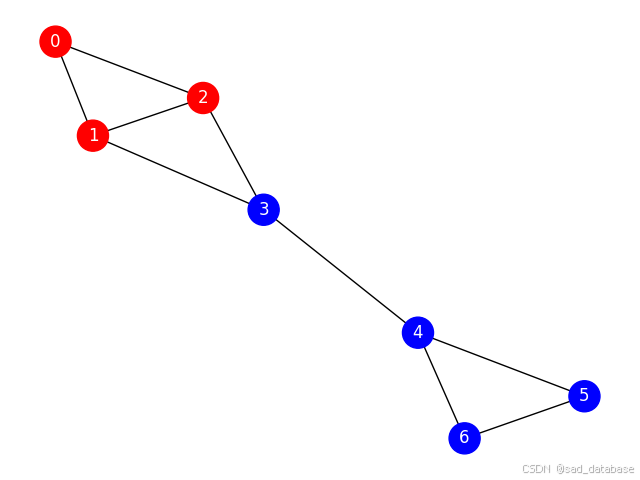
node_colors = ['red' if node in max_clique else 'blue' for node in G.nodes()]
pos = nx.spring_layout(G)

# 绘制节点和边
nx.draw(G, pos, with_labels=True, node_color=node_colors, node_size=500, font_color='white')

# 显示图形
plt.show()

输出结果：图的染色数 (χ(G)): 3
最大团的大小 (ω(G)): 3
利用染色数改进的最大团上界: 3

最大团定点用红色表示，其他用蓝色表示。