数据结构——树（搬运知识点以及一些简单的解释）

1、树是n (n≥0) 个结点的有限集, 如果n=0，称为空树；如果n>0

        (1)  有且仅有一个称为根的结点root

        (2)  n>1时，其余结点可分为m个互不相交的有限集T1 …  Tn，其中每一个集合又是一棵树，称为根的子树

2、度与节点

¯        （1）结点的度：结点拥有的子树的个数。

¯        （2）树的度：树内各结点的度的最大值。

¯        （3）叶结点：度为0的结点。

¯        （4）分支结点：度不为0的结点。

        3、节点的关系

           （1）孩子与双亲：结点的子树的根称为该结点的孩子，该结点称为孩子的双亲。

             (2)兄弟：同一双亲的孩子之间互称兄弟。

           （3）结点的祖先：从根到该结点所经分支上的所有结点。

           （4）结点的子孙：以某结点为根的子树中任一结点。

        4、路径与路径长度

        （1）路径：从根结点到其他结点的一条路经。

        （2）路径长度：路径经过的边的个数。

        

        5、层次与深度

        （1）结点层次：从根开始，根为第一层，根的孩子为第二层，以此类推。

        （2）树的深度：树中结点的最大层次。

        

        6、无序与有序

         如果树中各结点的子树从左至右是有次序的（不能互换），则称该树为有序树；否则为无序树。

简易理解（如果是无序树，则一般来说同样多节点的情况下，可以组成的有序树的数量会比无序树的多）

        7、同构 两棵树形状相同

二、二叉树

        

        1、定义

     n(n>=0)个结点的有限集合，该集合或者为空集，或者由一个根结点和两棵互不相交的左右子树组成。

特点

    （1）、每个结点最多只有两个子树

    （2）、左右子树次序不能颠倒（有序）

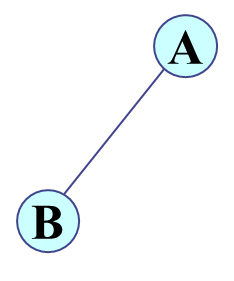
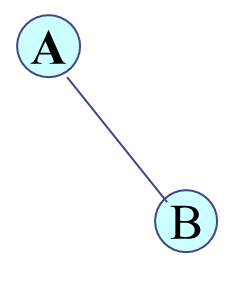 对于树来说，左右是同一颗树，却不是同一颗二叉树

2、二叉树具备5种形态

空树、单节点、单节点有左支、单节点有右支、单节点有左右支

3、特殊二叉树

（1）斜树：所有结点都只有左子树的二叉树称为左斜树；所有结点都只有右子树的二叉树称为右斜树。

（2）满二叉树所有的分支结点都存在左子树和右子树，并且所有叶子都在同一层上。

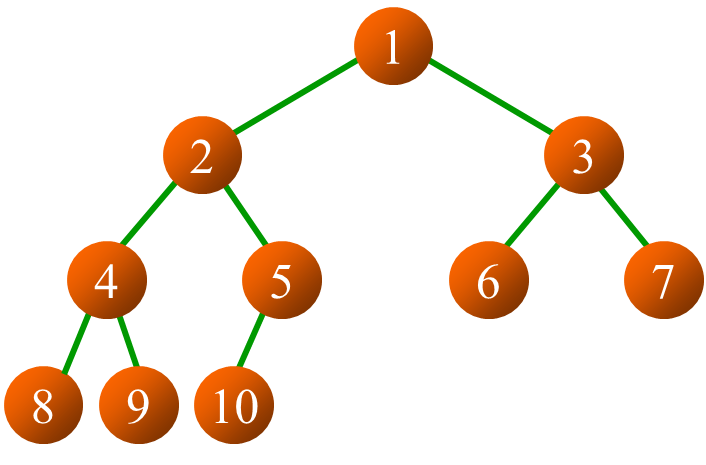（3）完全二叉树按从上到下、从左到右的顺序为结点编号，与满二叉树序号一一对应的二叉树。如图

4、性质

性质1：在二叉树的第i层上至多有 2的i-1 次方个结点(i≥1).

性质2：深度为 k 的二叉树至多有 2的k次方-1 个结点 (k≥0)。

性质3：任何一棵二叉树，如果其叶结点数为n0，度为2的结点数为n2，则n0=n2+1.

性质4：具有n个结点的完全二叉树的深度为+1。

 性质5：

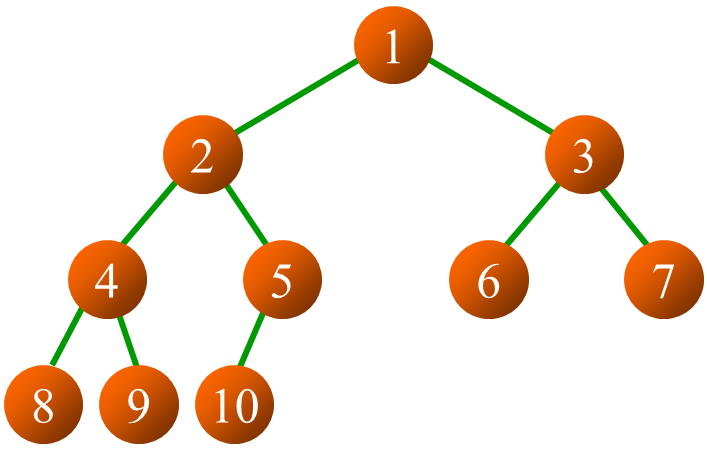
对含n个结点的完全二叉树从上到下，从左至右进行1至n的编号，则任意一个编号为i的结点：
(1) 如果i=1，为根；如果i>1，则其双亲为 [i/2]

 (2) 如果2i>n，则结点无左孩子，否则其左孩子为2i (2i 表示如果该树是满二叉树则当前编号为i的节点对应的左孩子节点为2i 比如图上的2 和4；若n=7，对于节点4而言 2i=8 >7 此时没有左孩子节点)

 (3) 如果2i+1>n，则无右孩子，否则其右孩子为2i+1（同上）

 三、树的遍历

 

1、前序遍历

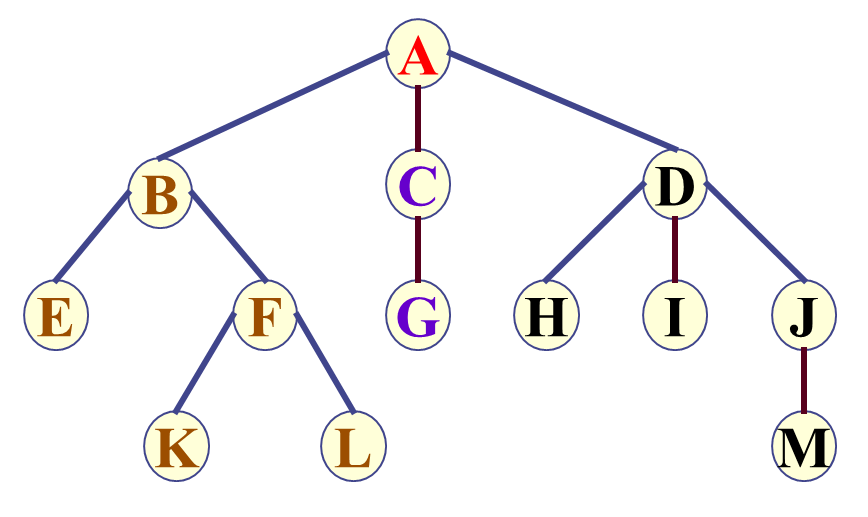
    （1）访问根结点

    （2）按照从左到右的顺序依次前序遍历根结点的每一棵子树。

遍历结果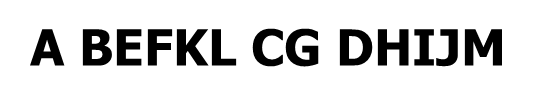 

2、后序遍历

    （1）按照从左到右的顺序依次后序遍历根结点的每一棵子树

    （2）访问根结点。

3、层序遍历（也称为广度遍历）

从第一层开始，从上到下逐层遍历，同层按从左到右的顺序遍历。

四、二叉树的遍历

 

1、前序遍历（DLR）

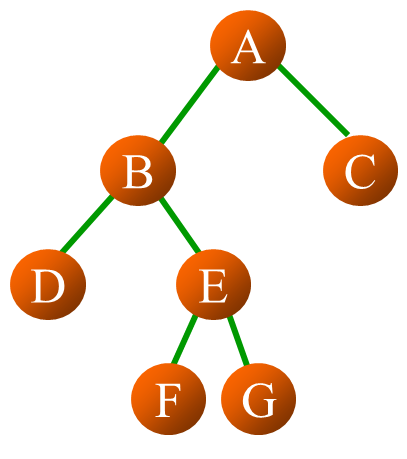
    （1）访问根结点

    （2）前序遍历左子树

    （3）前序遍历右子树

2、中序遍历（LDR）

    （1）中序遍历左子树

    （2）访问根结点

    （3）中序遍历右子树

 

3、后序遍历（LRD）

    （1）后序遍历左子树

    （2）后序遍历右子树

    （3）访问根结点

4、层序遍历（也称为广度遍历）

      从第一层开始，从上到下逐层遍历，同层按从左到右的顺序遍历