一、计数排序
问题引入
这里有一堆1-100的数,请对这些数字进行排序?
问题解决
ok这里的这些数字首先呢,是什么?范围是有限的,也就是说这些数最小是1 最大是100
我们可不可以用一个数组存储这些数?如果这个数是1,那就在数组的1位置上+1,以此类推
之后把数组从1-100依次排数,排到原数组里面即可
问题本质
问题的本质是什么?
对有范围的数进行排序,没错,有范围的数,然后呢在这个范围里,数字按照自己的大小进行入队,之后依次出队,这真的只是计数排序吗?
实则桶排序,详细看文章的第三点
代码
//桶排序
public class Count {
//计数排序 0~200
public static void countSort(int[] arr){
if (arr==null||arr.length<2)return;
//寻找数组最大值,然后设桶
int max=Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max=Math.max(max,arr[i]);
}
int []bucker=new int[max+1];
for (int i = 0; i < arr.length; i++) {
bucker[arr[i]]++;
}
int i=0;
for (int j = 0; j < arr.length; j++) {
while (bucker[j]>0){
arr[i++]=j;
bucker[j]--;
}
}
}
}
二、基数排序
我们有一堆数字,这些数字最大呢是五位数,怎么排序?
我们可以从个位开始,到千位,依次排序,谁的权重高?万位权重最高,万位最后排
简单的入桶
//基数排序
public static void radixSortQuick(int[] arr,int L,int R){
int max= (int) Long.MIN_VALUE;
for (int i = L; i <= R; i++) {
if (arr[i]>max)max=arr[i];
}
//最大数是几位数
int maxdigit=0;
while (max>0){
maxdigit++;
max/=10;
}
Queue<Integer>[] arrayList=new Queue[10];
for (int i = 0; i < 10; i++) {
//每一个位置都是null,我们如果不去初始化
// 那么在后面加数的时候会报错你让null.add
//null.pull什么的不就会错吗
arrayList[i]=new LinkedList<>();
}
//总循环,每次判断每一个位置上的排序
for (int i = 1; i < maxdigit + 1; i++) {
for (int j = L; j < R+1; j++) {
arrayList[getdigitnum(arr[j],i)].add(arr[j]);
}
int index=L;
//从arr的L开始 替换桶 桶怎么排数字?
//一个一个排就ok了,空了就break
//如下
for (int j = 0; j < 10; j++) {
while (!arrayList[j].isEmpty()){
arr[index++]=arrayList[j].poll();
}
}
}
}三、桶排序(计数与基数的底层及优化)
计数排序的本质
计数排序本质到底是什么?有人就好奇了,这个跟桶有什么关系?如果是基数排序,那确实跟桶有关,但是计数排序怎么有?
计数排序如果单单的是计数,那当然,与桶的关系不明显,但是如果是一个实体类,里面存储age或者有范围的数字的话,那可以计数吗?当然不可以了,那就是桶了,每一个位置上都是linklist,然后入链表
计数排序跟基数排序的关系
有人问了,计数排序跟基数排序有什么区别?都是排序数字,同时为啥会有这两种?
仔细来看基数排序是计数排序的进阶,为什么这么说?
首先计数排序是什么?对一个范围上的数进行排序
基数排序是什么?对多个位置上的数进行多次排序
ok,根据这两句话就可以判断出来,基数排序是多次的计数排序,计数排序里面的1-100这个范围,其实呢跟位数里面每一位都是0-9有什么区别吗?
除了范围加大了,本质上没什么区别。也就是说计数排序,其实就是范围大的基数排序里面多轮排序的一种情况
实际业务中,用户的年龄,类型等各种数据就是各种不同的范围,如果说这个范围可控,这个范围只有几个选项那就可以进行桶排序
所以,计数排序是单一范围但是范围较大的的基数排序
基数排序的优化
基数排序在干嘛?在入桶然后每个桶都出来,我们看图
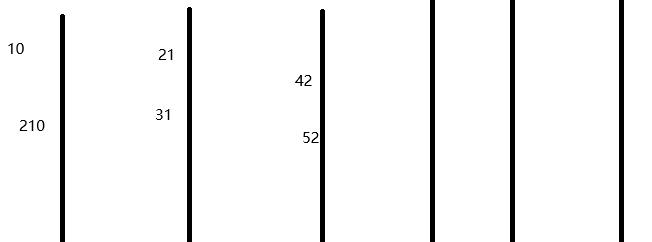
如上图所示,我们把所有数都入桶,是通过个位数判断入桶,之后呢,再一个一个的出桶,放到相应的位置上,因为我们是从左往右出桶,所以相关数可以放到正确的位置上。
如果已经经过了几轮的排序,先进的数字因为在前几轮的排序排好了后要排在后面数字的前面,所以先进的数字要先出。位置也正好对上。
但是这样的排序由于用的是分开的队列,内存不是连续的,内存的利用率,以及查询速度等,都比普通的连续地址的数组要慢很多,那么可以优化吗?答案是可以。
我们需要什么?需要的是确定当前数要放的位置,同时前面进的数要放前面,后面进的数要放后面。
位置怎么确定?我们想想,第一个位置上的数字是不是可以确定有几个?个位是0的可以确定个数,个位是1的也可以确定个数,如果个位是0 1 的个数相加是什么?是最右边的个位是1的数应该放的位置+1。比如上面图里面的31 出来应该放在数组的第四位,index是3,而 个位是0 1的总数是4
这是规律吗?是的
我们可以将其优化成数组排序,具体是这样的
首先进入该轮个位排序,数组统计每一种可能的数,然后再把数字的0加到1上,1位置上的数加到2上,此时数组存储的是该种数最后一个数该放的位置+1
之后从右往左遍历,判断什么位上的数,然后放置到help数组上这个数,然后help数组拷贝到原数组即可,多轮均这样即可。
代码如下
//基数排序隐式桶
public static void radixSort(int [] arr,int L,int R){
//首先我们算数组的最大位数是多少位
//其次每次算这个数在这个位上的数字
int max=(int) Long.MIN_VALUE;
for (int i = L; i <= R; i++) {
if (arr[i]>max)max=arr[i];
}
int maxdigit=0;
while (max>0){
max/=10;
maxdigit++;
}
int[] help=new int[R-L+1];
//每一位进行一次排序,占比最大的最后排序,比如会员和年龄 会员肯定优先,那么会员是后排
//会员在maxdigit这里 年龄在1这里 作为第一个进行排序的
for (int i = 1; i < maxdigit+1; i++) {
int count[]=new int[10];
for (int j = L; j < R+1; j++) {
//在某位上的count++
count[getdigitnum(arr[j],i)]++;
}
for (int j = 1; j < count.length; j++) {
count[j]=count[j-1]+count[j];
}
for (int j = help.length-1; j >=0 ; j--) {
//从count右到左,算自己位数是几位,然后放在help里面的第x-1处
//j+R是排序的树所在的位置,i是现在是排的那个位置上的 十位个位百位
//在help数组上放arr 位置是count数组计算这个数的所在位数上的值
//在count里面存了要放的位置
//测试
// int a=getdigitnum(arr[j+L],i);
// int b=count[getdigitnum(arr[j+L],i)];
// int c=j+L;
help[count[getdigitnum(arr[j+L],i)]-1]=arr[j+L];
count[getdigitnum(arr[j+L],i)]--;
}
for (int j = 0; j < help.length; j++) {
arr[j+L]=help[j];
}
}
}
//得到数字在d位上的值
public static int getdigitnum(int num,int d){
//pow是10的d-1次方
return ((num/((int)Math.pow(10,d-1)))%10);
}优化性能对比
测试代码如下,结果为百万数据优化了86%左右 一万数据优化了44% 将近一半
public static void main(String[] args) {
long all1=0;
long all2=0;
for (int i = 0; i < 100; i++) {
int[] arr1 = DuiShuQi.generate(10000, 1000);
//时长测试 隐式桶 显式桶
//一万是 37 60 30 57
//十万是 255 825 282 848
//一百万是 2296 15352 2288 14526
//一千万是 23000 208100 36915 262895
//也就是说一万是差两倍 一万耗时从 0.059 优化到了0.033s 优化了44%
//十万是三倍多 十万耗时从 0.84s 优化到了0.27s 优化了67.9%
//一百万是七倍 一百万耗时从 14.9s 优化到了2.3s 优化了86.6%
//一千万是八倍左右的差距 一千万的耗时从 235.5s 优化到了29.9s 优化了87.3%
//因为显式桶内存不是连续的
//内存间的跳跃耗时与数组中连续的空间时间不同
//同时由于显式桶内存是不连续的,对空间的利用率非常的不友好
//就像jvm里面已经拒绝了标记清除一样,我们这里需要拒绝这种断断续续的排序方式
int[] arr2 = arr1.clone();
//测试排序隐式桶的时间
long cur= System.currentTimeMillis();
//System.out.println("cur:"+cur);
radixSort(arr1,0,arr1.length-1);
all1+=System.currentTimeMillis()-cur;
//System.out.println("all1:"+all1);
//测试排序显示桶的时间
cur= System.currentTimeMillis();
radixSortQuick(arr2,0,arr2.length-1);
//System.out.println(cur);
all2+=System.currentTimeMillis()-cur;
//System.out.println(all2);
DuiShuQi.compare(arr1,arr2);
}
System.out.println("all1 "+all1);
System.out.println("all2 "+all2);
}四、资料链接
github链接,本文的代码为src下code05里面的count和radix类,用到的对数器是DuiShuQi文件夹下的类
项目的百度网盘链接 所处位置与github中的相同





















 1165
1165

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








