面试官：顺序表插入平均要挪几次？我推完公式他直接点头-优快云博客

1.顺序表的插入

#include <iostream>
using namespace std;

#define MaxSize 10 //定义最大长度
typedef struct {
	int data[MaxSize];  //用静态数组存放数据元素
	int length;  //顺序表的当前长度
}SqList;   //顺序表的类型定义


//初始化顺序表
void InitList(SqList& L) {
	L.length = 0;
}


//基本操作:在L的位序i处插入元素e
bool ListInsert(SqList& L, int i, int e) {
	if (i<1 || i>L.length + 1) {   //判断i的范围是否有效
		return false;
	}
	if (L.length > MaxSize) {   //当前存储空间已满,不能插入
		return false;
	}
	for (int j = L.length;j >= i;j--) {
		L.data[j] = L.data[j - 1];
	}
	L.data[i - 1] = e;
	L.length++;
	return true;
}


//打印顺序表
void PrintList(SqList L) {
	for (int i = 0;i < L.length;i++) {
		cout << L.data[i] << " ";
	}
	cout << endl;
}

int main() {
	SqList L;  //声明一个顺序表
	InitList(L);

	//插入测试
	ListInsert(L, 1, 10);
	ListInsert(L, 2, 20);
	ListInsert(L, 3, 30);
	ListInsert(L, 2, 15);

	PrintList(L);

	return 0;
}

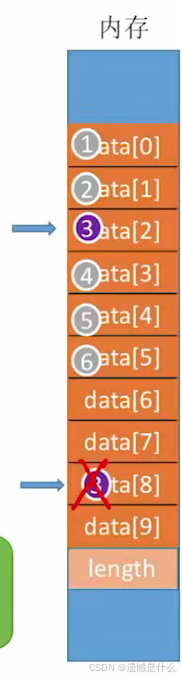下面for循环的这组代码:
首先定义j为数组长度, 如右图所示, 长度为length 为5;
现在要在3的位置也就是数组下标为2的位置(data[2])插入一个数;
需要原来在3位置的数向后挪动一个长度, 将data[4]的数据放在5的位置(现在的j就变为了4), 将data[3]的数据放在4的位置(现在的j就变为了3);
又因为j >= i, 所以只进行两次循环;
最后length++(长度由5变为了6)

for (int j = L.length;j >= i;j--) {
	L.data[j] = L.data[j - 1];
}
L.data[i - 1] = e;
L.length++;

2.时间复杂度的计算
最好情况：新元素插入到表尾，不需要移动元素
i = n + 1，循环 0 次；最好时间复杂度 = O(1)
最坏情况：新元素插入到表头，需要将原有的 n 个元素全都向后移动
i = 1，循环 n 次；最坏时间复杂度 = O(n)
平均情况：假设新元素插入到任何一个位置的概率相同，即 i = 1, 2, 3, …, length + 1 的概率都是 p = 1/(n+1)
i = 1，循环 n 次；i = 2，循环 n - 1 次；i = 3，循环 n - 2 次；…；i = n + 1，循环 0 次
平均循环次数 = n·p + (n - 1)·p + (n - 2)·p + … + 1·p = n(n + 1)/2 · 1/(n + 1) = n/2
平均时间复杂度 = O(n)

2.顺序表的删除

#include <iostream>
using namespace std;

#define MaxSize 10
typedef struct {
	int data[MaxSize];
	int length;
}SqList;


void InitList(SqList& L) {
	L.length = 0;
}

//插入元素(先插入才能删除)
bool ListInsert(SqList& L, int i, int e) {
	if (i<1 || i>L.length+1) {
		return false;
	}
	if (L.length > MaxSize) {
		return false;
	}
	for (int j = L.length;j >= i;j--) {
		L.data[j] = L.data[j - 1];
	}
	L.data[i - 1] = e;
	L.length++;
	return true;
}


//删除元素
bool ListDelete(SqList& L, int i, int& e) {
	if (i<1 || i>L.length) {
		return false;
	}
	e = L.data[i - 1];
	for (int j = i;j < L.length;j++) {
		L.data[j - 1] = L.data[j];
	}
	L.length--;
	return true;
}

void PrintList(SqList L) {
	for (int i = 0;i < L.length;i++) {
		cout << L.data[i] << " ";
	}
	cout << endl;
}

int main() {
	SqList L;
	InitList(L);

	//插入一些数据
	for (int i = 1;i <= 5;i++) {
		ListInsert(L,i, i * 10);    //插入10,20,30,40,50
 
	}
	cout << "删除前:";
	PrintList(L);

	int deletedValue;
	if (ListDelete(L, 3, deletedValue)) {
		cout << "删除成功,被删元素为:" << deletedValue << endl;

	}
	else {
		cout << "删除失败" << endl;

	}

	cout << "删除后为:";
	PrintList(L);

	return 0;
	 
}

Attation:

//插入元素(先插入才能删除)
bool ListInsert(SqList& L, int i, int e)

//删除元素
bool ListDelete(SqList& L, int i, int& e)

注意插入元素和删除元素:插入直接使用e,删除则为引用e(&e)

//插入元素(先插入才能删除)
bool ListInsert(SqList& L, int i, int e) {
	if (i<1 || i>L.length+1) {
		return false;
	}
	if (L.length > MaxSize) {
		return false;
	}
	for (int j = L.length;j >= i;j--) {
		L.data[j] = L.data[j - 1];
	}
	L.data[i - 1] = e;
	L.length++;
	return true;
}


//删除元素
bool ListDelete(SqList& L, int i, int& e) {
	if (i<1 || i>L.length) {
		return false;
	}
	e = L.data[i - 1];
	for (int j = i;j < L.length;j++) {
		L.data[j - 1] = L.data[j];
	}
	L.length--;
	return true;
}

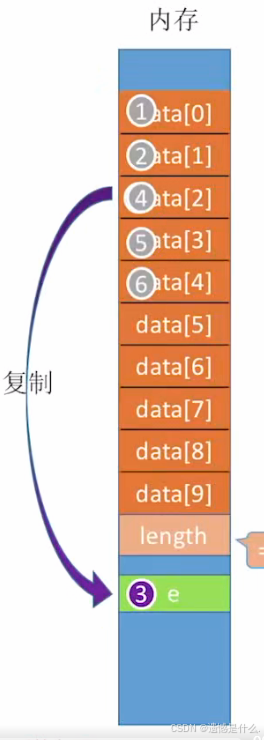
注意两个函数中的for循环:

1.插入元素时j >= i;j--;删除元素时j < L.length;j++;

2.插入元素时是后面的元素先往后挪动;删除元素时是前面的元素先向前挪动

3.插入元素时L.length++;删除元素时L.length--;

顺序表删除的时间复杂度

最好情况：删除表尾元素，不需要移动其他元素
i = n，循环 0 次；最好时间复杂度 = O(1)
最坏情况：删除表头元素，需要将后续的 n - 1 个元素全都向前移动
i = 1，循环 n - 1 次；最坏时间复杂度 = O(n)
平均情况：假设删除任何一个元素的概率相同，即 i = 1, 2, 3, …, length 的概率都是 p = 1/n
i = 1，循环 n - 1 次；i = 2，循环 n - 2 次；i = 3，循环 n - 3 次；…；i = n，循环 0 次
平均循环次数 = (n - 1)p + (n - 2)p + … + 1·p = n(n - 1)/2 · 1/n = (n - 1)/2
平均时间复杂度 = O(n)

3.顺序表的按位查找

#include <iostream>
using namespace std;

typedef int ElemType;

#define InitSize 100

typedef struct {
	ElemType* data;   //指示动态分配数组的指针
	int MaxSize;    //最大容量
	int length;   //当前长度
}SeqList;

ElemType GetElem(SeqList L, int i) {
	return L.data[i - 1];   //顺序表内部0号单元存储第1个元素
}

int main() {
	SeqList L;
	L. data = new ElemType[InitSize];
	L.MaxSize = InitSize;
	L.length = 5;

	for (int j = 0;j < L.length;j++) {
		L.data[j] = (j + 1) * 10;
	}
	cout << "第三个元素为:" << GetElem(L, 3) << endl;
	return 0;
}

顺序表的按位查找时间复杂度为:O(1).

4.顺序表的按值查找

#include <iostream>
using namespace std;

typedef int ElemType;
#define InitSize 100

typedef struct {
	ElemType* data;
	int MaxSize;
	int length;
}SeqList;

int LocateElem(const SeqList& L, ElemType e) {   // 加 const& 避免拷贝
	for (int i = 0;i < L.length;i++) {
		if (L.data[i] == e) {
			return i + 1;
		}
	}
	return 0;
}

int main() {
	SeqList L;
	L.data = new ElemType[InitSize];
	L.MaxSize = InitSize;
	L.length = 6;

	for (int i = 0;i < L.length;i++) {
		L.data[i] = (i + 1) * 10;
	}

	ElemType key = 30;              // 用变量保存要查找的值
	int pos = LocateElem(L, key);
	if (pos) {
		cout << "元素:" << key << "的位序为:" << pos << endl;
	}

	delete[] L.data;
	return 0;
}

时间复杂度:

最好情况：目标元素在表头
循环1次；最好时间复杂度 = O(1)
最坏情况：目标元素在表尾
循环n次；最坏时间复杂度 = O(n)
平均情况：假设目标元素出现在任何一个位置的概率相同，都是 1/n
目标元素在第1位，循环1次；
在第2位，循环2次；
…
在第n位，循环n次
平均循环次数 =
1·(1/n) + 2·(1/n) + … + n·(1/n)
= (1 + 2 + … + n) / n
= [n(n + 1)/2] / n
= (n + 1)/2
平均时间复杂度 = O(n)