栈和队列
引言
- 在任意第i(i=1,2,…n,n+1)个位置插入新元素,或删除任意第i(i=1,2,…n)个元素受限的数据结构---- 即插入和删除受限制的线性表。
- 主要有:栈、队列、线性表
栈
- 限定在表尾作插入、删除操作的线性表。
- 栈的有关术语:
- 进栈 :插入一个元素到栈中。 或称:入栈、推入、压入、push。
- 出栈:从栈删除一个元素。 或称:退栈、上托、弹出、pop。
- 栈顶:允许插入、删除元素的一端(表尾)。
- 栈顶元素:处在栈顶位置的元素。
- 栈底:表中不允许插入、删除元素的一端。
- 栈底元素:处在栈底的元素。
- 空栈:不含元素的栈。
- 先进后出:栈的元素进出规则。
- 栈一些别名:“后进先出”表、“LIFO”表(Last In First Out)、反转存储器、地窖、堆栈。

栈的基本操作:
(1) Initstack(s): 置s为空栈。 //初始化栈
(2) Push(s,e): 元素e进栈s。 //进栈
若s已满,则发生溢出。
若不能解决溢出,重新分配空间失败,则插入失败。
(3) Pop(s,e): 删除栈s的顶元素,并送入e 。 //入栈
若s为空栈,发生“下溢”(underflow);
为空栈时,表示某项任务已完成。
(4) Gettop(s,e): 栈s的顶元素拷贝到e。 //取元
若s为空栈,则结束拷贝。
(5) Empty(s): 判断s是否为空栈。 //判空
若s为空栈,则Empty(s)为true;否则为false。
................
栈的存储表示和操作实现
-
顺序栈: 用顺序空间表示的栈。
-
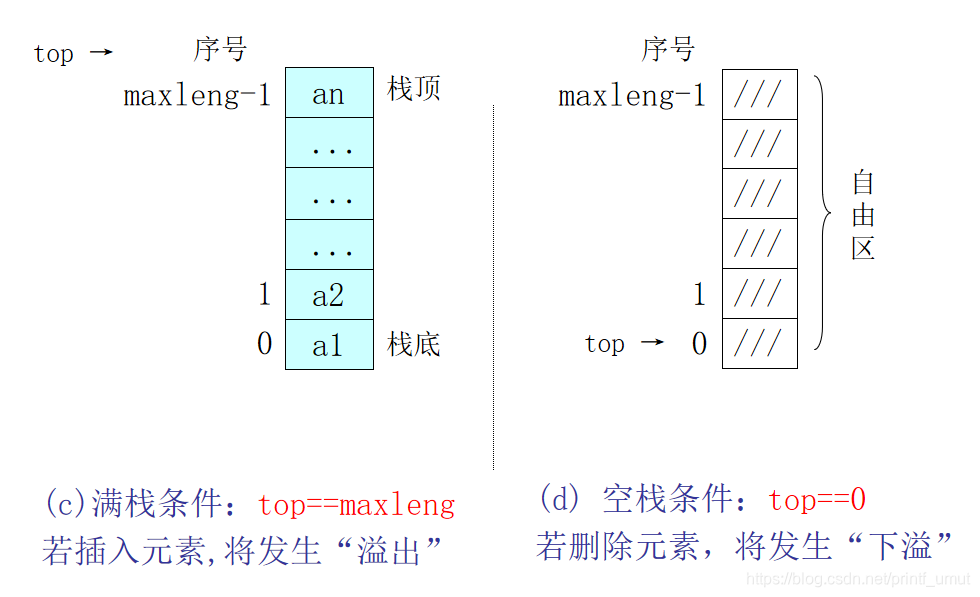
方案一:栈空间范围为:s[0…maxleng-1]
顶指针指向顶元素所在位置:- 进栈操作:先对top加1,指向下一空位置,将新数据送入top指向的位置,完成进栈操作。结束时top指向新栈顶元素所在位置。
- 出栈操作:先对top减1,根据top指向取出栈顶数据元素。完成出栈操作。结束时top指向去掉原栈顶元素后的新栈顶元素所在位置的上一空位置。


-
方案二:栈空间范围为:s[0…maxleng-1]
顶指针指向顶元素上的一空位置:- 进栈操作:先将新数据送入top指向的位置,再对top加1,指向下一空位置,完成进栈操作。结束时top正好指向新栈顶元素所在位置的上一空位置。
- 出栈操作:先对top减1,根据top指向取出栈顶数据元素。完成出栈操作。结束时top指向去掉原栈顶元素后的新栈顶元素所在位置的上一空位置。

-
存储空间的分配
(a) 静态分配
typedef struct
{ ElemType elem[maxleng]; //栈元素空间
int top; //顶指针
}sqstack; //sqstack为结构类型
sqstack s; //s为结构类型变量
// 其中: s.top---顶指针;s.elem[s.top-1]---顶元素(方案二)
b) 动态分配
#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
typedef struct
{ ElemType *base; //指向栈元素空间
int top; //顶指针
int stacksize; //当前分配的栈空间大小
} SqStack; // SqStack为结构类型
SqStack s; //s为结构类型变量
// 其中: s.top--顶指针;s.base[s.top-1]--顶元素(top也是0开始)
- 基本算法:
(1)初始化栈(动态分配)
void InitStack(SqStack &S)
{
S.base=(ElemType *)malloc(STACK_INIT_SIZE*sizeof(ElemType));
S.top=0;
S.stacksize= STACK_INIT_SIZE;
}
(2) 进栈算法 (约定:top指向栈顶元素上一位置)
int push(SqStack &S,ElemType x)
{
if (S.top>=S.stacksize) //发生溢出,扩充
{
newbase=(ElemType *)realloc(S.base,
(S.stacksize+STACKINCREMENT)*sizeof(ElemType));
if (!newbase){
printf(“Overflow”);
return ERROR;} //无可分配空间(一般不用考虑)
S.base=newbase;
S.stacksize+=STACKINCREMENT;
}
S.base[S.top]=x; //装入元素x
S.top++; //修改顶指针
return OK;
(3) 出栈算法
int pop(SqStack &S, ElemType &x)
{
if (S.top==0)
return ERROR; //空栈
else
{
S.top--; //修改顶指针
x= S.base[S.top]; //取走栈顶元素
return OK; //成功退栈,返回OK
}
}
- 链式栈:
- 使用不带头结点的链表
//定义
struct node
{ ElemType data; //data为抽象元素类型
struct node *next; //next为指针类型
} *top=NULL; //初始化,置top为空
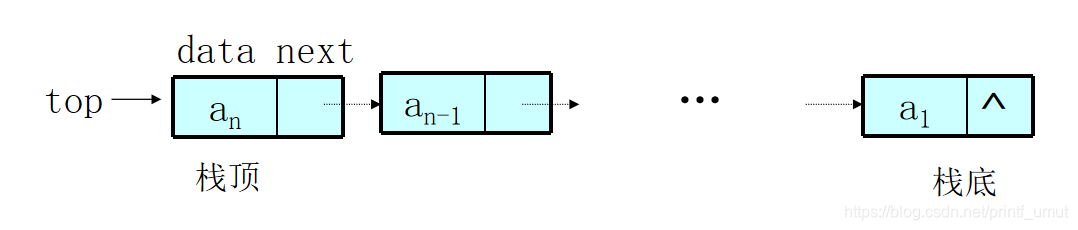
非空链式栈的一般形式:
假定元素进栈次序为:a1、a2、…an。
用不带表头结点的单链表时:
- 进栈需要找到最后一个结点。
- 出栈时删除最后一个结点。
- 缺点:进出栈时间开销大: O(n)

解决方案:将指针次序颠倒过来,top指向an。
- 进栈将新结点作为首结点。
- 出栈时删除首结点。
- 优点:进出栈时间为常数: O(1)
(1)进栈操作
struct node *push_link(struct node *top,Elemtype e)
{ struct node *p;
p=(struct node *)malloc(sizeof(struct node));//生成新结点
p->data=e; //装入元素e
p->next=top; //插入新结点
top=p; //top指向新结点
return top; //返回指针top
}
(2)退栈操作
struct node *pop(struct node *top,Elemtype *e) //或 &e
{ struct node *p;
if (top==NULL) return NULL; //空栈,返回NULL
p=top; //p指向原栈的顶结点
(*e)=p->data; //取出原栈的顶元素送(*e)
//也可e=p->data 此时函数应该传e的地址 &e
top=top->next; //删除原栈的顶结点
free(p); //释放原栈顶结点的空间
return top; //返回新的栈顶指针top
}

队列
- 只允许在表的一端删除元素,在另一端插入元素的线性表。
- 队列有关术语:
- 空队列:不含元素的队列。
- 队首:队列中只允许删除元素的一端。head,front
- 队首元素:处于队首的元素。
- 队尾:队列中只允许插入元素的一端。rear,tail
- 队尾元素:处于队尾的元素。
- 进队:插入一个元素到队列中。又称:入队。
- 出队:从队列删除一个元素。
- 先进先出:队列中元素的进出原则。
- 其他别名:“先进先出”表,“FIFO” 表(First In First Out),排队,queue

队列的基本操作:
(1)InitQueue(q)---- 初始化,构造一个空队列q。
(2)QueueEmpty(q)----判断q是否为空队列。
(3)EnQueue(q,e)---- 将e插入队列q的尾端。
(4)DeQueue(q,e)---- 取走队列q的首元素,送e。
(5)GetHead(q,e)---- 读取队列q的首元素,送e。
(6)QueueClear(q)----置q为空队列。
.................
- 双队列
- (1)双队列----允许在表的两端插入、删除元素的线性表。

- (2) 输出受限双队列----只许在表的两端插入、在一端删除元素的线性表。

- (3)输入受限双队列----只允许在表的一端插入、在两端删除元素的线性表。

链队列
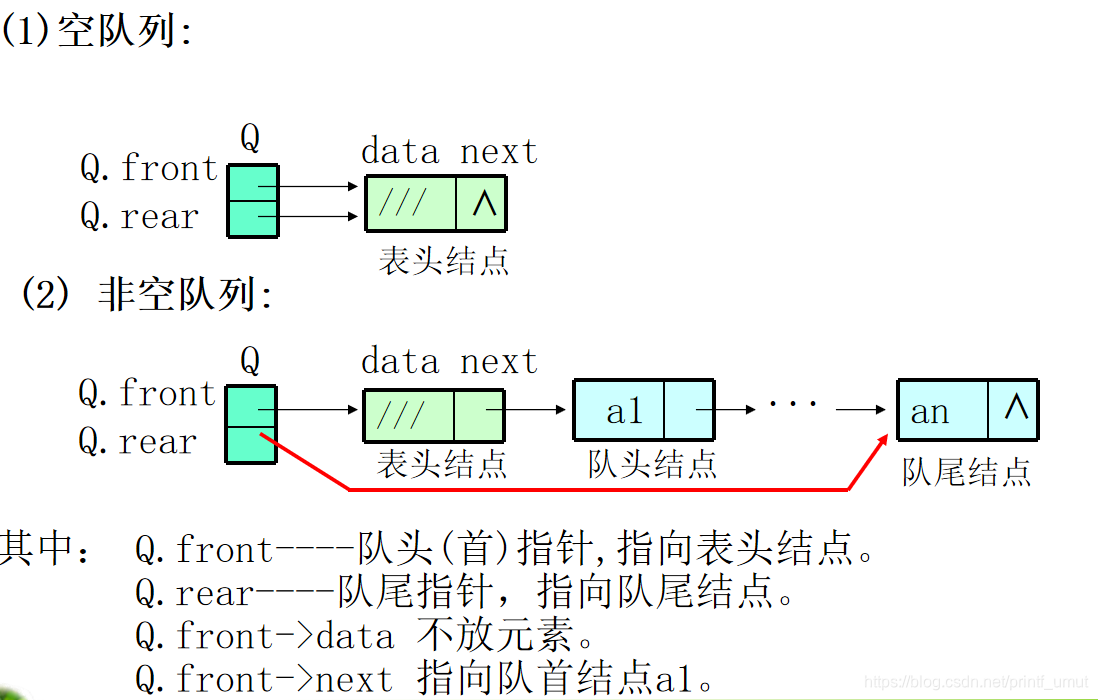
定义
//存放结点的结点定义
typedef struct Qnode
{ ElemType data; //data为抽象元素类型
struct Qnode *next; //next为指针类型
}Qnode,*QueuePtr; //结点类型, 指针类型
//其中:Qnode----结点类型
//QueuePtr----指向Qnode的指针类型
//由头、尾指针组成的结点类型
typedef struct
{ Qnode *front; //头指针
Qnode *rear; //尾指针
}LinkQueue; //链式队列类型

队列有关基本算法:
#define LENG sizeof(Qnode) //求结点所占的单元数
(1)生成空队列
LinkQueue InitQueue( ) //生成仅带表头结点的空队列Q
{ LinkQueue Q; //说明变量Q
Q.front=Q.rear=(QueuePtr)malloc(LENG);//生成表头结点
Q.front->next=NULL; //表头结点的next为空指针
return Q; //返回Q的值
}
(2)插入元素
LinkQueue EnQueue(LinkQueue Q, ElemType e)
{ Qnode *p; //说明变量p
p=(Qnode *)malloc(LENG); //生成新元素结点
p->data=e; //装入元素e
p->next=NULL; //为队尾结点
Q.rear->next=p; //插入新结点
Q.rear=p; //修改尾指针
return Q; //返回Q的新值
}
(3)插入算法(2)
int EnQueue(LinkQueue *Q, ElemType e) //传参不同
{ Qnode *p; //说明变量p
p=(Qnode *)malloc(LENG); //生成新元素结点
if (!p) {printf(“OVERFLOW”); //新结点生成失败
return ERROR;}
p->data=e; //装入元素e
p->next=NULL; //为队尾结点
Q->rear->next=p; //插入新结点
Q->rear=p; //修改尾指针
return OK; //成功返回
(4)出栈算法
Status DelQueue(LinkQueue &Q, ElemType &e)
{ Qnode *p; //说明变量p
if (Q.front==Q.rear) //若原队列为空
{printf(“Empty queqe”); //空队列
return Q;}
p = Q.front->next; //P指向队头结点
e = p->data; //取出元素,e指向它
Q.front->next=p->next; //删除队头结点
if (Q.rear==p) //若原队列只有1个结点
Q.rear=Q.front; //修改尾指针
free(p); //释放被删除结点的空间
return OK;
进栈

出栈
 顺序队列
顺序队列
- 用一维数组表示队列
- 需要解决的问题: 假溢出

解决假溢出的方法一: 移动元素:每次将要溢出时,f,r均往前移删除元素个数个位置。

(常用)解决假溢出的方法二: 将Q当循环表使用(循环队列):

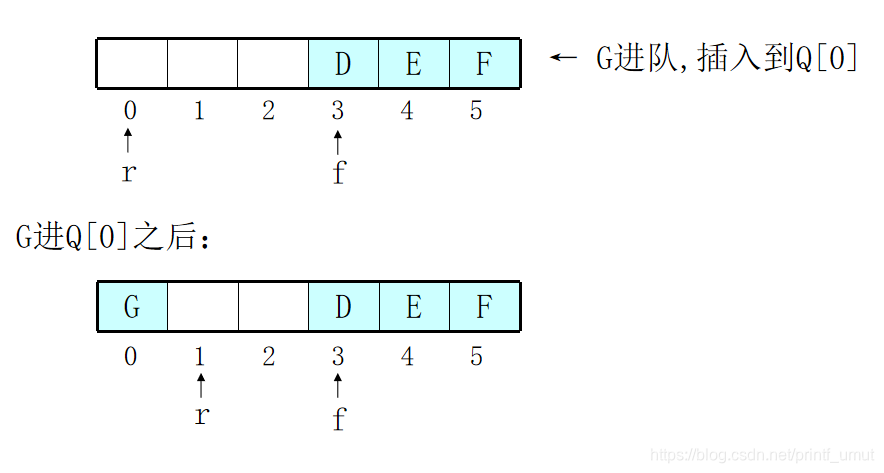
方法二的实现:
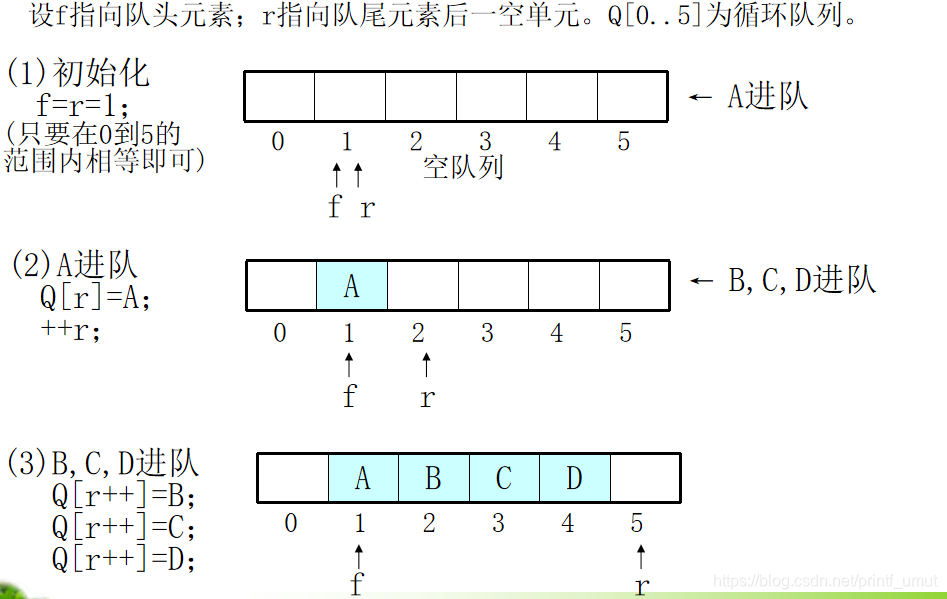
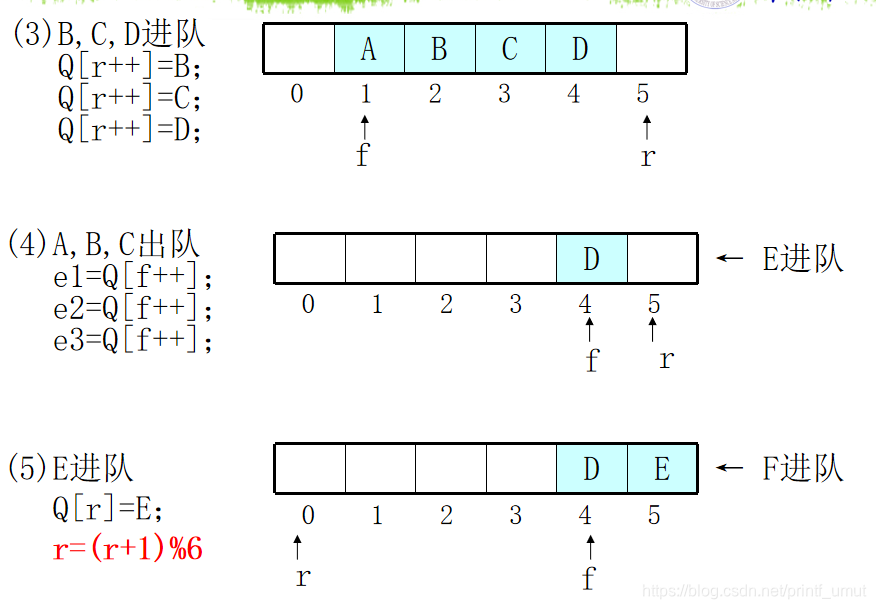

方法二的实现中遇到小问题:二义性 即空队列与满队列定义相同。
解决方案:
- 方案一:增加一个标识变量
- (常用) 方案二:还剩最后一个单元不使用,可避免满队列时出现的二义性,即: 进队前测试:若r+1==f,表明还剩最后一个单元,认为此时就是满队列。
- 若队列为Q[0…maxleng-1], 则共有maxleng-1个元素

重要语句:
- 若队列为Q[0…maxleng-1], 则共有maxleng-1个元素
- r=(r+1)%6 循环对列入队时尾指针的移动
- (r+1)%maxleng==f 循环队列为满队列的判定(r等于f时 才为空)
顺序队列基本操作的 代码实现
- 采用 循环队列 留空解决二义性 (常用)
1)进队算法:
//假设用Q表示顺序队列,头指针front指向队头元素,rear指向尾元素的后一个空位,e为进队元素。
int En_Queue( SeQueue &Q,Elemtype e)
{ if ((Q.rear+1)% MAXLENG==Q.front) //若Q已满,退出
return ERROR;
Q.elem[Q.rear]=e; //装入新元素e
Q.rear++; //尾指针后移一个位置
Q.rear = Q.rear % MAXLENG; //为循环队列
return OK;
}
(2)出队算法
int De_Queue(SeQueue &Q,Elemtype &e)
{
if (Q.front==Q.rear) //Q为空队列,退出
return ERROR;
e=Q.elem[Q.front]; //取走队头元素,送e
Q.front=(Q.front+1)% MAXLENG;//循环后移动尾指针
return OK;
}
进队(两种已满情况)

出队






















 4970
4970

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








