递归，深搜，回溯，剪枝算法讲解

1，什么是递归？

递归，就是函数自己调用自己，然后在某些特定的条件下给递归设置一个递归出口，不要形成死递归：

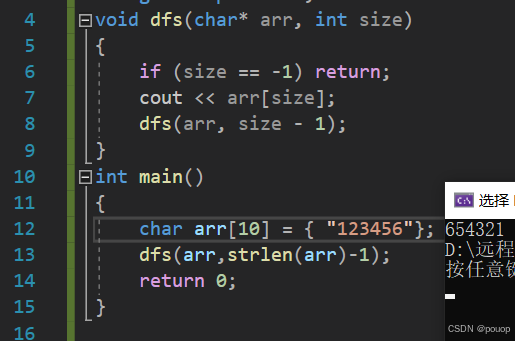
图中dfs函数就是利用自己调用自己的方式倒着打印数组的内容，出口就是在dfs中用if条件判断出口标准。

2，为什么用递归？

在我们写算法的时候，会发现某些问题需要重复大量的使用同一种方法来完成我们的目的，这个时候我们可以有两种选择，第一种是循环，第二种就是递归，这两种方法各有利弊，如果有人写过算法的可能会了解到有时候用循环会很方便，有时候用递归很方便，但是如果从递归转成循环或者循环转成递归就是一个大工程，那么我们如何从题目中分辨到底是用递归还是循环？

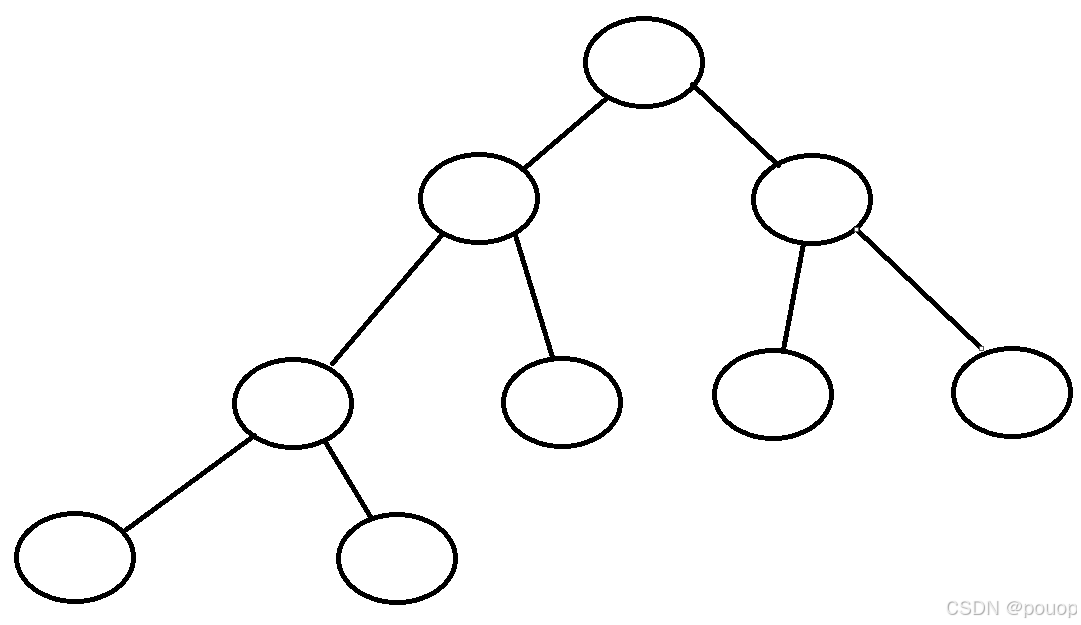
如上图所示，如果一个函数会形成多个分支来完成我们的子问题，我们用循环来解决的话就会需要借助栈的帮助，非常麻烦，这个时候递归的优势就体现出来了

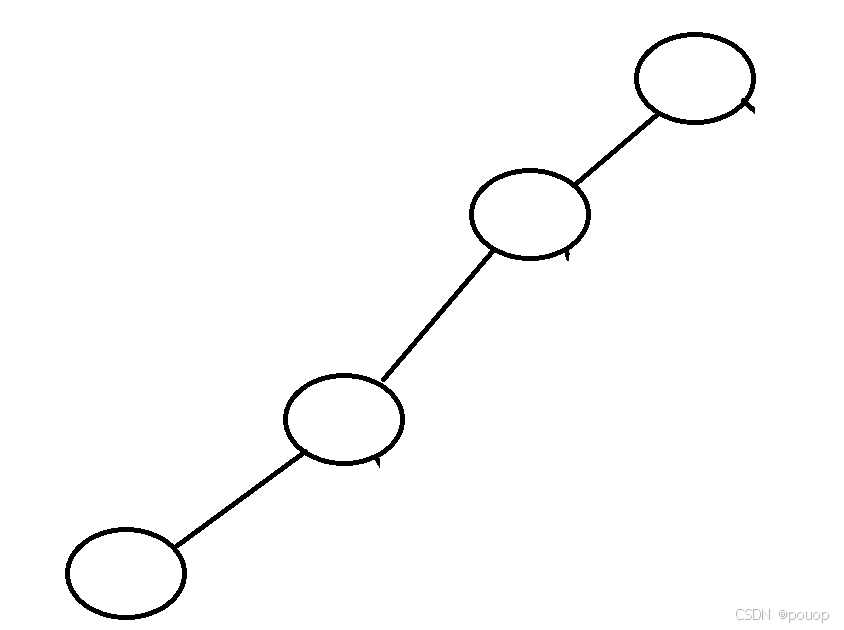
但是如上图所示，函数整体都只是往一个方向走，这个时候虽然递归也可以解决问题，但是不如循环来的方便，以上就是在题目中递归和循环的选择。

3，如何理解递归？

我们用归并排序来举例子理解递归：

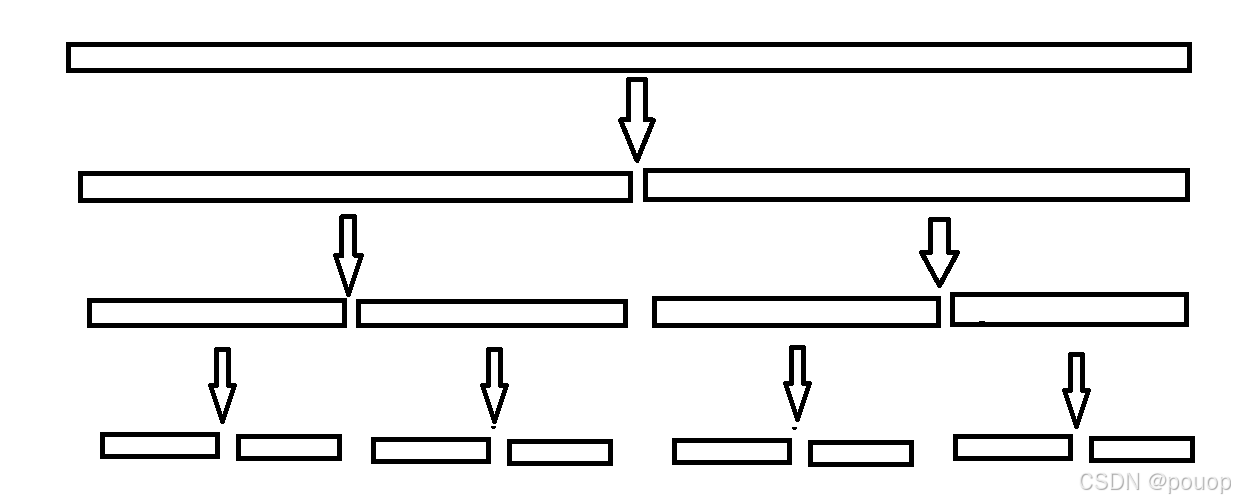
可以看到上图，长方形代表需要排序的数组，把他分成两半一半排完序之后和另一半排完序的数组组合在一起，然后被分的数组也变成两份之后排序，以此类推，这就是递归的用法。

4，如何写好一个递归？

1，先找到相同的子问题（决定了函数头的设计）

2，只关系某一个子问题在干什么（决定了函数体的设计）

这里面需要穿插一个很重要的思想：黑盒，把我们设计的递归相信他，一定能帮我们解决后面的问题，然后去设计函数体就行。

（往后的名词简写：深度遍历：dfs，宽度遍历：bfs，我们的重点是dfs）

3，细节问题（函数出口，环境清理等）

5，深度搜索

看到图中的二叉树，利用中序后序等遍历一遍二叉树中的内容就叫做深度搜索

6，回溯与剪枝

回溯的本质就是深搜，在搜索时发现路径和需要完成的目标不一致则返回的过程，在二叉树遍历中也存在着回溯。

剪枝就是回到分叉路时，若知道有路已经走过并且走不通的时候，我们把他咔掉，下一次来时就不会找到这条路这种方法叫做剪枝。

（在递归中加上全局变量，在递归中或许会有奇效）以下是我完成的几道例题可以拿来参考）

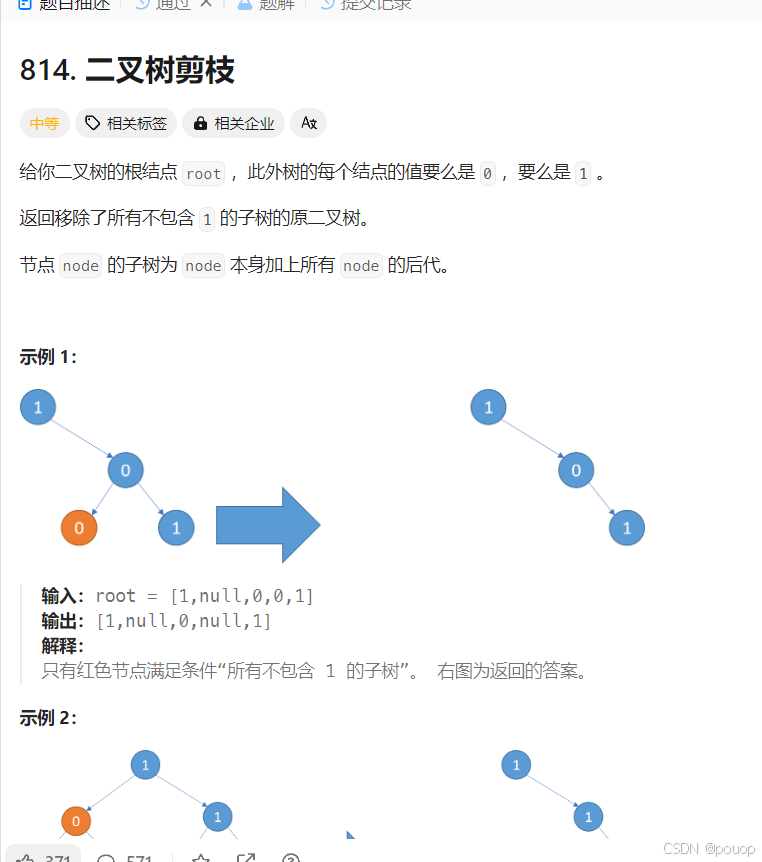
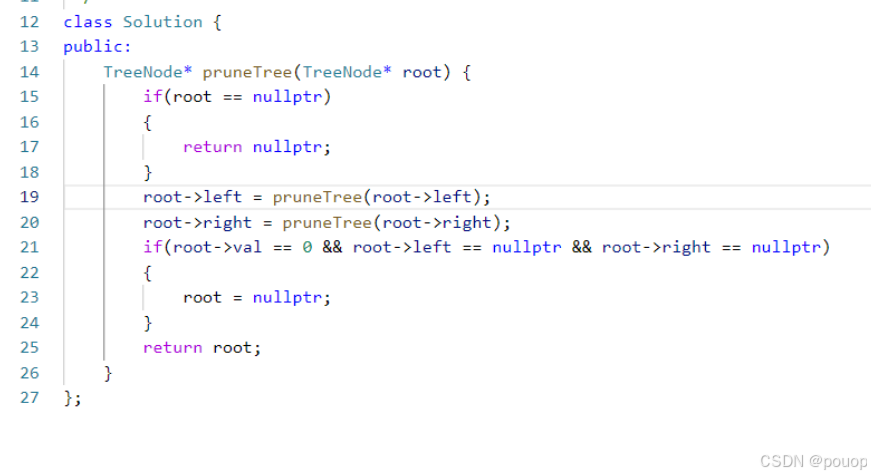
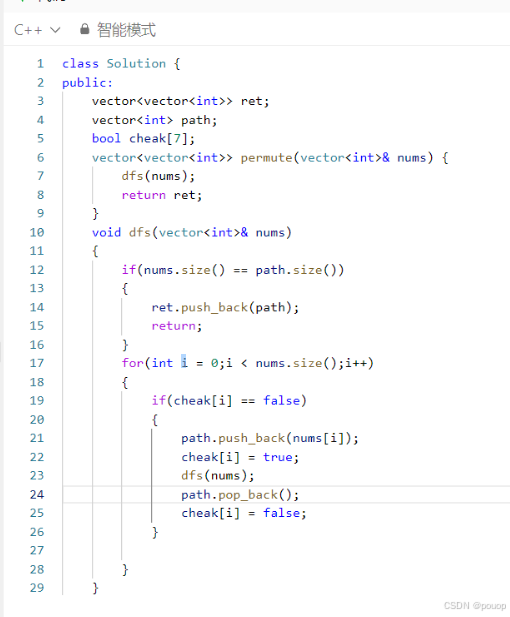
其中fds函数体中path.pop_back()就是环境清理，这是在利用全局变量时需要注意的点，当然如果把path放到函数递归函数中就不用进行函数清理，看哪种更适合就可以用哪一种。

上面全排列中还利用到了boll数组来辅助我们完成递归函数体的设计

希望对你们的算法能力有所帮助。