知识点---递归

定义

递归算法是一种直接或者间接调用自身函数或者方法的算法。

递归算法的实质是把问题分解成规模缩小的同类问题的子问题，然后递归调用方法来表示问题的解。递归算法对解决一大类问题很有效，它可以使算法简洁和易于理解。

递归算法，其实说白了，就是程序的自身调用。它表现在一段程序中往往会遇到调用自身的那样一种coding策略，这样我们就可以利用大道至简的思想，把一个大的复杂的问题层层转换为一个小的和原问题相似的问题来求解的这样一种策略。

递归往往能给我们带来非常简洁非常直观的代码形势，从而使我们的编码大大简化，然而递归的思维确实很我们的常规思维相逆的，我们通常都是从上而下的思维问题， 而递归趋势从下往上的进行思维。这样我们就能看到我们会用很少的语句解决了非常大的问题，所以递归策略的最主要体现就是小的代码量解决了非常复杂的问题。

递归算法解决问题的特点：

• 递归就是方法里调用自身。
• 在使用递归时，必须有一个明确的递归结束条件，称为递归出口。
• 递归算法解题通常显得很简洁，但递归算法解题的运行效率较低，所以一般不提倡用递归算法设计程序。（用递归能实现的用循环也能实现）
• 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储，递归次数过多容易造成栈溢出等，所以一般不提倡用递归算法设计程序。

示例：阶乘

循环写法：

public class Factorial {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("number = ");
        int num = scanner.nextInt();
        int result = 1;
        for (int i = 1; i <= num; i++) {
            result *= i;
        }
        System.out.println("Factorial(" + num + ")=" + result);
    }
}

递归写法：

不过，这个函数的问题是，它会永远运行下去，因为它没有终止的地方。函数会连续不断地调用 factorial。 当计算到零时，没有条件来停止它，所以它会继续调用零和负数的阶乘。因此，我们的函数需要一个条件，告诉它何时停止。
　　由于小于 1 的数的阶乘没有任何意义，所以我们在计算到数字 1 的时候停止，并返回 1 的阶乘（即 1）。因此，真正的递归函数类似于：

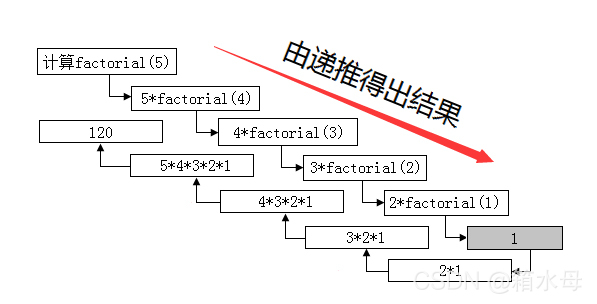
可见，只要初始值大于零，这个函数就能够终止。

要有一个明确的递归结束条件。

停止的位置称为 基线条件（base case）。基线条件是递归程序的最底层位置，在此位置时没有必要再进行操作，可以直接返回一个结果。所有递归程序都必须至少拥有一个基线条件，而且 必须确保它们最终会达到某个基线条件；否则，程序将永远运行下去，直到程序缺少内存或者栈空间。

public class Factorial1 {
    public static int factorial(int num){
        if (num == 1){
            return 1;
        }
        return  num * factorial(num - 1);
    }
}

public class demo {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("num = ");
        int num = scanner.nextInt();
        System.out.println(Factorial1.factorial(num));
    }
}

二分法查找

二分法查找效率很高，但是输入的序列必须提前排好序。

循环：

public static int binarySearch(int[] arr, int value) {

        int low = 0; // 开始位置
        int high = arr.length - 1; // 结束 位置

        while(low <= high) {
            int middle = (low + high) / 2;

            if (value == arr[middle]) {
                return middle; //返回查询到的索引位置
            }

            if (value > arr[middle]) {
                low = middle + 1;
            }

            if (value < arr[middle]) {
                high = middle - 1;
            }
        }
        //上面循环完毕，说明未找到，返回-1
        return -1;
    }

}

递归：

public static int binSearch(int[] array, int start, int end, int key){
        int mid = (end - start) / 2 + start;
        if (array[mid] == key){
            return mid;
        }
        if (start >= end){
            return  -1;
        }
        else if (key > array[mid]){
            return  binSearch(array, mid + 1, end, key);
        }
        else if (key < array[mid]){
            return binSearch(array, start, mid - 1, key);
        }
        return -1;
    }