数据表示
数据编码与表示
- 需要在计算机中表示的对象
程序,整数,浮点数,字符(串),逻辑值
通过编码表示 - 表示方式
用数字电路的两个状态表示
由上一层抽象计算机来识别不同的内容 - 编码原则
少量简单的基本符号
一定的规则
表示大量复杂的信息
方便使用
编码表示
- 基本元素
0,1两个基本符号 - 字符
26个字母->5位
大/小写+其他符号=7bits(in 8)
世界上其他语言的文字=16bits(unicode) - 无符号整数(0,1,…, 2 n − 1 2^{n}-1 2n−1)
- 逻辑值
0—false 1—true - 颜色
- 位置/地址/指令
- 但n为只能代表 2 n 2^{n} 2n个不同的对象
逻辑型数据
- 逻辑
true 真
false 假 - 数据表示
1
0 - 数据运算
- 与,或,非
| x | y | x与y | x或y | x的非 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
字符型数据
-
重要的人机界面
-
由符号组成
为每个符号进行编码,由输入/输出设备进行转换
一般以字符串的形式在计算机存储器中存放 -
字符集编码标准
ASCII
UNICODE
UTF-8 -
ascii字符编码
采用7位二进制编码,占用一个字节
表示128个西文字符
ascii码字符集
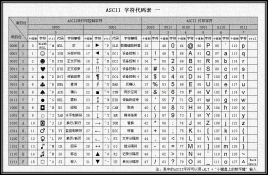
-
unicode编码
使用16位表示一个字符,可表示65536个字符
将整个编码空间划分为块,每块为16的整数倍,按块进行分配
保留6400个码点供本地使用
依然无法覆盖所有字符 -
utf-8编码
| 字符位数 | 字节1 | 字节2 | 字节3 | 字节4 | 字节5 | 字节6 |
|---|---|---|---|---|---|---|
| 7 | 0ddddddd | |||||
| 11 | 110ddddd | 10dddddd | ||||
| 16 | 1110dddd | 10dddddd | 10dddddd | |||
| 21 | 11110ddd | 10dddddd | 10dddddd | 10dddddd | ||
| 26 | 111110dd | 10dddddd | 10dddddd | 10dddddd | 10dddddd | |
| 31 | 1111110d | 10dddddd | 10dddddd | 10dddddd | 10dddddd | 10dddddd |
变长字符编码,提高存储空间利用率
字符长度由首字节确定
字符首字节外,均以“10”开始,可自同步
可扩展性强
成为互联网上占据统治地位的字符集
数值型数据表示
-
定点数
小数点位置固定
整数
定点小数 -
浮点数
小数点位置浮动 -
整数的二进制表示
二进制的两个状态0和1
n位可得到 2 n 2^{n} 2n种组合,可表示 2 n 2^{n} 2n个整数
| 机内表示 | 真值 |
|---|---|
| 0 | 0 |
| 01 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| … | … |
| 1{n} | 2 n − 1 2^{n}-1 2n−1 |
- 评价标准
- 无符号数
- 表示范围
- 直观
- 便于算术运算的实现
-
- 有符号数
表示范围
直观
正负平衡
便于算术运算的实现
- 有符号数
进位计数法
进位计数法
∑
i
=
m
−
k
D
i
R
i
\sum_{i=m}^{-k}{D_{i}R^{i}}
∑i=m−kDiRi
N表示某个数值
r表示这个数的基数
i表示这些符号排列的位号
D
i
D_{i}
Di是位号为i的位上的一个符号
r
i
r^{i}
ri是位号i的位上的一个1代表的值
- 常用的数制
十进制,二进制,八进制,十六进制
进制与进位计数法
二进制
r=2,基本符号 0 1
八进制
r=8,基本符号0 1 2 3 4 5 6 7
十进制
r=10,基本符号0 1 2 3 4 5 6 7 8 9
十六进制
r=16,基本符号0 1 2 3 4 5 6 7 8 9 A B C D E F
计算机采用二进制
二进制整数的进位表示法
具体到n位无符号二进制整数,如
b
n
−
1
b
n
−
2
.
.
.
b
1
b_{n-1}b_{n-2}...b_{1}
bn−1bn−2...b1
其中
b
i
b_{i}
bi为0或1
表示的值为N=
∑
i
=
0
n
−
1
b
i
2
i
\sum_{i=0}^{n-1}{b_{i}2^{i}}
∑i=0n−1bi2i
可表示的范围为0------
2
n
−
1
2^{n}-1
2n−1,共
2
n
2^{n}
2n个数。
如何表示有符号整数
- 需要有1位来表示符号位
最高位
0表示整数,1表示负数 - 其他位表示数据
原码 反码 补码
负数表现形式
原码:符号位||数的绝对值
反码:符号位||数值
补码:反码的最低位+1
| 编码 | 原码 | 反码 | 补码 |
|---|---|---|---|
| 000 | 0 | 0 | 0 |
| 001 | 1 | 1 | 1 |
| 010 | 2 | 2 | 2 |
| 011 | 3 | 3 | 3 |
| 100 | -0 | -3 | -4 |
| 101 | -1 | -2 | -3 |
| 110 | -2 | -1 | -2 |
| 111 | -3 | -0 | -1 |
补码的性质
补码与真值的对应
- 补码求真值
N= − b n − 1 ∗ 2 n − 1 + ∑ i = 0 n − 2 b i 2 i -b_{n-1}*2^{n-1}+\sum_{i=0}^{n-2}{b_{i}2^{i}} −bn−1∗2n−1+∑i=0n−2bi2i - 真值求补码
正数的补码是绝对值原码
负数的补码是绝对值原码按位求反后,再在最低位加1 - 补码的加法运算
加法运算 符号位和数据位同样计算
[x+y]补=[x]补+[y]补
[x]补与[-x]补
[x]补在同符号位内,逐位求反,再在最低位加1,即可得[-x]补
补码减法
[x-y]补=[x]补+[-y]补
大端与小端
0x12345678
小端 78 56 34 12 大端 12 34 56 78

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








