《统计学习方法》之感知机代码实现（原始形式和对偶形式）

    下图是一个典型的二分类问题，如果现在需要建立模型来根据数据点的$x_1,x_2$的值对它所属的类别进行判定该怎么做？

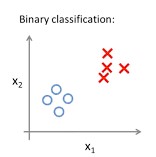
    通过观察，被标为叉的数据点的$x_1,x_2$的取值均较大，那是否可以通过计算$x_1+x_2$的值来对数据进行分类，答案是可以的，这时模型就可以表示为
$$f(x)=sign(x_1+x_2-k)$$
$$sign(x)=\{\begin{array}{ll}X(被标记为叉)& x>=0\\ O(被标记为圈)& x<0\end{array}$$
    这时模型中的$k$值是未知的，我们可从已有的数据点中学习k，具体来说就是计算出所有数据点对应的$x_1+x_2$，被标为圆圈的数据点对应的和的最大值为$k_{min}$，被标为叉的数据点对应的和的最小值为$k_{max}$，这样如果我们将模型中的k设定为区间$(k_{min},k_{max}]$中的某个值时，我们的模型就能够成功预测所有已知的样本点的类别。以上得到的模型就是一个感知机模型。这个例子中我们是简单粗暴地通过直接观察数据点分布的方法确定了模型中各个数据维度对应的权重，通过计算确定了k可能的取值的范围。如果数据是多维的，难以直接观察时，我们就需要更科学的方法进行学习。
    如上所述，感知机模型，就是一种线性分类模型，模型对应的是一个能够将数据点进行线性划分的分离超平面。
    下面是模型的函数表示，f(x)即为模型对应的判别函数，w,b为模型的参数，sign为符号函数，非负数输出+1，否则为-1。
$$f(x)=sign(w^{T}x+b)$$
    如我们上面的例子所述，通常情况下对于一个线性可分的数据集，我们的K的取值可以有无穷多个，也就是存在多个感知机模型能够线性分割数据集，怎么确定哪个是我们最想要的？这时我们就需要定义一种选择的策略，具体来说就是通过定义损失函数，选择那个使得损失函数最小的模型。
$$L=\sum _{x_i\in M}\frac{1}{||w||}|w\cdot x_i+b|$$
    这里的M表示的就是误分类的点组成的集合，损失函数的含义就是所有误分类的点到超平面的距离的和。定义好了损失函数然后就是通过梯度下降法最小化损失函数。求梯度之前还需做一件事就是去除L中的绝对值符号，因为y的取值只有两种可能+1或-1，对于所有误分类的点而言，y取+1时$w\cdot x_i+b$为负值，y取-1时$w\cdot x_i+b$为正值，所以损失函数也可表示为如下形式：
$$L=-\sum _{x_i\in M}\frac{1}{||w||}{y}_i(w\cdot x_i+b)$$
忽略L中的$\frac{1}{||w||}$，然后求出参数的梯度可得：
$${\nabla }_{w}L(w,b)=-\sum _{x_i\in M}{y}_i{x}_i$$

$${\nabla }_{b}L(w,b)=-\sum _{x_i\in M}{y}_i$$
每次更新时选取一个误分类的点，对w，b进行更新：
$$w\leftarrow w+\eta y_i{x}_i$$

$$b\leftarrow w+\eta y_i$$
综合以上可得感知机算法的原始形式：

    为什么叫感知机？这篇博客给出了一些原因，但是我个人觉得可以把它理解为这个模型的训练是对输入数据的感知过程。因为从直观上理解，在训练过程中，当一个实例点被误分类后，超平面就会向该实例点移动，直到该实例点被正确分类，这个过程我认为就是一个感知的过程，一开始模型对空间数据的分布一无所知，在感知到数据分布后不断调整自身参数，最后得到一个能够将数据正确分类的模型。

完整代码(求解原问题和对偶问题)：

#!/usr/bin/env python
# -*- encoding: utf-8 -*-
import numpy as np


def sign(x):
    if x >= 0:
        return 1
    else:
        return -1


class Perceptron:
    # 感知机模型，支持两种学习方式，原始求解和对偶问题求解
    def __init__(self, learning_rate, max_iter=1000):
        # 设置学习率
        self.learning_rate = learning_rate
        # 设置最大的迭代轮数
        self.max_iter = max_iter
        # 权重和偏置先设为None
        self.weight = None
        self.bias = None
        # 用于对偶问题学习
        self.alpha = None

    def fit(self, X, y):
        # 根据数据训练感知机模型
        # X 每一行是一个样本
        n, m = X.shape  # 表示有n个样本，每个样本为一个m维向量
        self.weight = np.zeros(m)  # 初始化权重为0
        self.bias = 0  # 初始化偏置为0
        for i in range(self.max_iter):
            # 每一轮迭代都从头开始找，直到找到分类错误的样本
            for j in range(n):
                if (np.sum(self.weight * X[j]) + self.bias) * y[j] <= 0:  # 找到分类错误的样本
                    # 使用分类错误的样本更新权重和偏置
                    self.weight += self.learning_rate * y[j] * X[j]
                    self.bias += self.learning_rate * y[j]
                    break  # 更新完成后可以选择break，下一次又重头开始找，也可以选择不break但是这样max_iter的含义就有所不同

    def fit_dual(self, X, y):
        # 求解感知机的对偶问题
        # Question: 为什么要提出对偶问题？
        # 一种解释为:
        # 考虑m很大，n很小的情况，也就是单条数据的维度很大，而数据量很小
        # 这种情况下使用原问题求解每次判断需要计算w*x，这样计算复杂为O(m)
        # 而使用这种办法，预先计算好Gram矩阵的情况下，判断时需计算Gram[j]*self.alpha*y，O(n)
        n, m = X.shape
        # 先计算出任意两个X向量的内积，也就是Gram矩阵
        Gram = np.zeros((n, n))
        for i in range(n):
            for j in range(n):
                Gram[i][j] = np.sum(X[i] * X[j])
        # alpha矩阵初始化为全0
        # alpha[i]/self.learning_rate表示第i个样本被用于更新梯度的次数
        self.alpha = np.zeros(n)
        self.bias = 0
        for i in range(self.max_iter):
            for j in range(n):
                if (np.sum(Gram[j] * self.alpha * y) + self.bias) * y[j] <= 0:  # 分类错误
                    # 样本j被用于更新梯度就加一个learning_rate
                    # 应为alpha/learning_rate表示的才是被用于梯度更新的次数
                    self.alpha[j] += self.learning_rate
                    self.bias += self.learning_rate * y[j]
                    break
        # 通过self.alpha计算self.weight，用于预测
        # 注意这里的求和，X.T每一列表示一个样本，self.alpha和y相乘后结果的shape为(1, n)
        # self.alpha的y相乘后的结果再乘X.T可理解为对所有样本进行加权求和
        self.weight = np.sum(self.alpha * y * X.T, axis=1)

    def predict(self, X):
        pred = []
        for i in range(len(X)):
            pred.append(sign(np.sum(self.weight * X[i]) + self.bias))
        return np.array(pred)


if __name__ == "__main__":
    X = np.array([[3, 3], [4, 3], [1, 1]])
    y = np.array([1, 1, -1])
    model = Perceptron(learning_rate=1)
    # model.fit(X, y)
    model.fit_dual(X, y)
    print("参数为:", model.weight, model.bias)
    print("预测结果为:", model.predict(X))