高级前端应该掌握的数学知识-矩阵

矩阵在图形学中非常重要，是必须要掌握的。将一些元素排列成若干行，每行放上相同数量的元素，就是一个矩阵。数学中矩阵长下面这样。

上图中是一个 m 行和 n 列（m * n）排列成的矩形阵列，在图形学中用的都是方块矩阵，也就是矩阵的行数和列数相等。在编程中我们通常将矩阵用一个普通数组或二维数组表示，就像下面这样。

const matrix1 = [1, 2, 3,1, 2, 3,1, 2, 3
]
const matrix2 = [[1, 2, 3],[1, 2, 3],[1, 2, 3]
] 

本系列文章中将只使用第一种一个简单一维数组表示矩阵，因为它更加紧凑。

矩阵加法和减法

两个矩阵相加就是将两个矩阵上对应位置的数相加即可，所以必须保证两个矩阵的尺寸相等，也就是说行要一样大小，列也要一样大小。

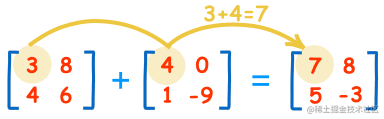
矩阵减法和加法一样，可以看成加一个负数。

矩阵乘法

矩阵最重要就是它的乘法，首先常量和矩阵的乘法比较简单，就是用常量乘以矩阵中的每个数就行了，这里不做过多介绍。主要讲解矩阵乘以矩阵，另外矩阵是没有除法的。

矩阵和矩阵的乘法稍微复杂一点，需要用到上篇文章中介绍的点积，运算的时候需要将第一个矩阵的第一行点积第二矩阵的第一列，就像下面这样。

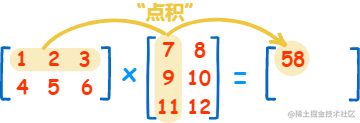
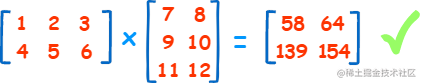
我们可以将第一行和第一列都看成一个上篇文章中介绍的矢量。第一个矩阵的第一行点积第二个矩阵的第一列得到的就是新矩阵的第一行和第一列的值，如果是第一个矩阵的第一行点积第二个矩阵的第二列，那么得到的就是新矩阵的第一行第二列的值。

这里的规律是新矩阵值的位置是第一个矩阵的行和第二个矩阵的